¶ Bao hàm loại trừ
Người viết:
- Phạm Vũ Phương - Trường THPT Chuyên Hà Tĩnh, Hà Tĩnh.
Reviewer:
- Đoàn Quang Huy - THPT Chuyên Nguyễn Tất Thành, Quãng Ngãi.
- Võ Đức Đoàn - THPT Chuyên Nguyễn Tất Thành, Quãng Ngãi.
- Nguyễn Tấn Minh - Trường Đại học Khoa học Tự nhiên, ĐHQG-HCM.
Trong giới lập trình thi đấu, nguyên lý Bao hàm – Loại trừ (Principle of Inclusion-Exclusion, viết tắt là PIE) là một công cụ toán học rất hữu ích để giải các bài toán đếm, đặc biệt là các bài toán có sự xuất hiện của các tập hợp có phần chung chồng chất nhau.
Qua bài viết này, bạn đọc sẽ được tìm hiểu kỹ hơn về nguyên lý Bao hàm -- Loại trừ và cách lập luận dựa trên phương pháp này để giải quyết các bài tập Lập trình thi đấu liên quan qua một số bài toán minh họa.
¶ Bài toán mở đầu
Giả sử ta có một tập hữu hạn và ba tập con . Để tính khi đôi một rời rạc nhau, ta chỉ việc cộng . Tuy nhiên, khi các tập hợp này tồn tại phần chung, phép cộng này sẽ đếm thừa, vì các phần tử thuộc , , đã bị đếm hai lần và các phần tử thuộc bị đếm ba lần.
Để giải quyết các phần bị đếm thừa, ta có thể trừ đi:
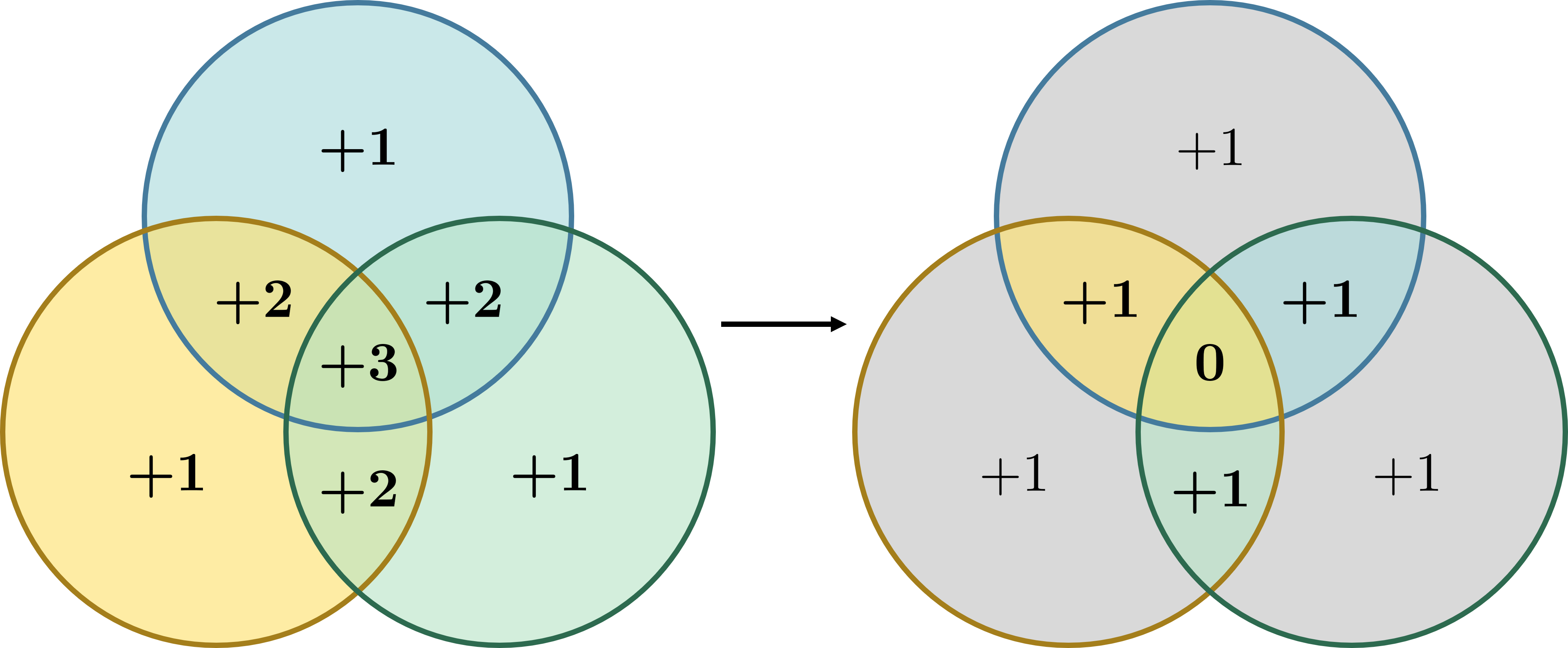
Lúc này phép đếm đã gần đúng, ngoại trừ các phần tử thuộc — sau khi được cộng 3 lần lại bị trừ ba lần. Do đó, ta cần cộng lại một lần nữa. Kết quả là:
Ví dụ minh họa
Trong một lớp học có:
- 30 học sinh thích Toán (tập )
- 25 học sinh thích Lý (tập )
- 20 học sinh thích Hóa (tập )
Ngoài ra:
- Có 10 học sinh thích cả Toán và Lý (ký hiệu: ).
- Có 8 học sinh thích cả Toán và Hóa (ký hiệu: ).
- Có 5 học sinh thích cả Lý và Hóa (ký hiệu: ).
- Có 3 học sinh thích cả ba môn (ký hiệu: ).
Hỏi có bao nhiêu học sinh thích ít nhất một trong ba môn Toán, Lý, Hóa? ()
Ta áp dụng công thức vừa nêu ở trên:
Vậy có 55 học sinh thích ít nhất một trong ba môn Toán, Lý, Hóa.
Nguyên lý bao hàm – loại trừ giúp ta mở rộng cách tính này để giải quyết các trường hợp tổng quát hơn, khi có nhiều tập hợp cùng tham gia.
¶ Nguyên lý Bao hàm - Loại trừ
¶ Công thức dạng tập hợp
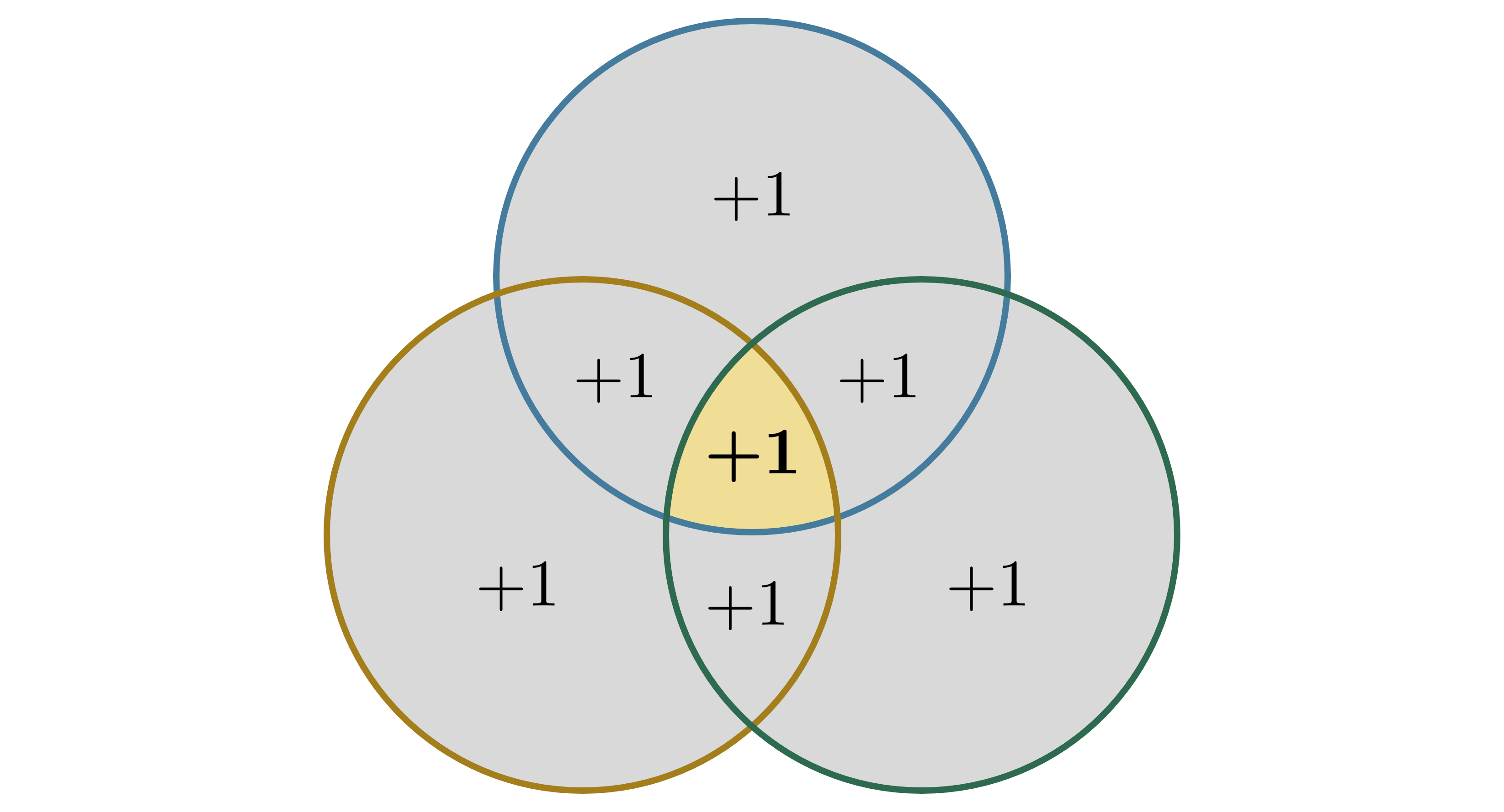
Khi tổng quát lên tập, gọi là các tập con của . Ta có công thức:
Công thức này phát biểu rằng để tính kích thước của hợp các tập , ta xét tất cả các tập con khác rỗng của . Mỗi tập con tương ứng với giao giữa các tập có chỉ số thuộc .
Dấu của mỗi số hạng được xác định bởi lực lượng của :
- Nếu lẻ, thì số hạng đó được cộng vào tổng.
- Nếu chẵn, thì số hạng đó được trừ ra.
Nhờ vậy, phép tính kích thước của một hợp lớn được chuyển thành việc tính kích thước các giao nhỏ hơn.
Chứng minh
Việc chứng minh tính đúng đắn của công thức này không khó: ta chỉ cần kiểm tra xem một phần tử được đếm bao nhiêu lần ở cả hai vế.
-
Nếu , thì nó được đếm đúng một lần ở mỗi vế.
-
Giả sử , và cụ thể hơn, thuộc đúng tập trong số .
- Ở vế trái, số lần đếm là .
- Ở vế phải, số lần đếm là:
Vì vậy, hai vế bằng nhau.
Cài đặt
int Union = 0;
for (int mask = 0; mask < (1 << n); mask++) {
// mask biểu diễn một tập con S của {0, 1, ..., n-1}
// intersect[mask] = | ⋂_{i ∈ S} A_i |
// __builtin_parity(mask) trả về:
// 1 nếu số bit bật trong mask là lẻ (|S| lẻ)
// 0 nếu số bit bật trong mask là chẵn (|S| chẵn)
if (__builtin_parity(mask))
Union += intersect[mask]; // |S| lẻ ⇒ cộng
else
Union -= intersect[mask]; // |S| chẵn ⇒ trừ
}
Khi không nhất thiết phải lấy hợp của tất cả các tập , ta có thể mở rộng nguyên lý bao hàm–loại trừ cho bất kỳ tập con chỉ số .
Khi đó, ta chỉ xét các tập với . Công thức bao hàm–loại trừ trong trường hợp này trở thành:
Ta có thể tính giá trị trên với mọi bằng trick duyệt bitmask trong hoặc DP SoS (bạn đọc có thể tham khảo cách tính qua bài VNOI Wiki này).
¶ Công thức dành cho xác suất
Nếu ta có biến cố , là xác suất của biến cố , xác suất của biến cố hợp của chúng (nghĩa là biến cố "có ít nhất một trong số biến cố xảy ra") là
Nếu gọi là tập hợp các tập hợp , công thức này cũng có thể viết gọn như sau:
¶ Mở rộng nguyên lý Bao hàm - Loại trừ
¶ Khôi phục từ điều kiện phủ định
Một ứng dụng rất điển hình của nguyên lý bao hàm–loại trừ là trong các bài toán đếm số phần tử thỏa một tập điều kiện cho trước khi bản thân các điều kiện này rất khó đếm trực tiếp, nhưng các phủ định của chúng thì lại dễ đếm hơn.
¶ Bài toán
Để hiểu rõ hơn về các dạng bài này, ta tìm hiểu bài toán Chia kẹo Euler có chặn trên được phát biểu như sau:
Cho hai số nguyên là số viên kẹo và số người nhận kẹo. Mỗi người có một giới hạn về số kẹo mà người đó được nhận được, được cho bởi dãy . Hãy đếm số cách chia viên kẹo thỏa mãn các giới hạn.
Nói cách khác, ta cần đếm số dãy sao cho với mọi và tổng bằng đúng .
Giới hạn:
- .
- .
¶ Phân tích
Với các công cụ tổ hợp quen thuộc, ta có thể giải quyết bài toán Chia kẹo Euler có chặn dưới một cách dễ dàng, tức người thứ phải nhận ít nhất viên kẹo. Tuy nhiên, điều tương tự không xảy ra với bài toán được phát biểu như trên.
Do đó, thay vì tìm kết quả trực tiếp cho bài toán Chia kẹo Euler có chặn trên, ta sẽ giải quyết bài toán dễ hơn rồi tìm cách áp dụng Bao hàm loại trừ để bù trừ ra đáp án cần tìm. Trước khi tiếp tục với ý tưởng lời giải, chúng ta tìm hiểu nhanh lời giải của bài toán Chia kẹo Euler có chặn dưới.
¶ Bài toán có điều kiện phủ định: Chia kẹo Euler có chặn dưới
Đếm số dãy sao cho với mọi và tổng bằng đúng . Trong trường hợp này, ta chọn .
Với bài toán Chia kẹo Euler cơ bản, ta có . Khi này, ta có thể biến đổi quá trình chia kẹo thành chọn "vách ngăn" để chia các viên kẹo thành nhóm. Do có tổng cộng cách ngăn, số cách chọn là:
Với , ta có thể mô hình quá trình chia kẹo lại với bước sau:
- Với người nhận thứ , ta đặt trước vào viên kẹo.
- Chia số kẹo còn lại theo bài toán Chia kẹo Euler cơ bản. Khi này, số kẹo mià mỗi người nhận được sẽ là .
Dễ thấy, số kẹo còn lại sau bước 1 là , do đó, đáp án của bài toán lúc này là:
Lưu ý, cách này vẫn đúng với , khi đó, ta hình dung người nhận sẽ "nợ" 1 viên kẹo ở bước đầu tiên. Do mỗi người đều sẽ nhận ít nhất 1 viên kẹo ở bước chia thứ hai nên phần "nợ" sẽ luôn được triệt tiêu.
¶ Ý tưởng
Khi đã giải được bài toán với điều kiện phủ định của bài toán ban đầu, ta tìm cách bù trừ để tìm kết quả.
Có thể thấy, nếu bài toán chỉ có một điều kiện cận trên (ví dụ chỉ người có giới hạn ) thì ta có thể nghĩ ngay đến cách bù trừ đơn giản: đếm số cách mà người đó nhận ít nhất viên, rồi trừ khỏi tổng số cách chia không ràng buộc.
Tuy nhiên trong bài toán này ta có tới điều kiện cận trên đồng thời. Việc xử lý từng điều kiện một sẽ khiến việc tính toán là vô cùng phức tạp, do đó, ta phải dùng nguyên lý bao hàm – loại trừ.
¶ Áp dụng Bao hàm -- loại trừ
Ta biến đổi bài toán thành đếm số cách chia kẹo bị vi phạm ít nhất một trong các điều kiện . Do đây là phần bù của tập nghiệm cần tìm, nên ta chỉ việc lấy tổng số cách chia, trừ đi số lượng cách chia bị vi phạm là có được đáp án cần tìm.
Để mô hình hoá, ta định nghĩa là tập các cách chia mà , tức vi phạm cận trên của người thứ ; những người còn lại có thể bị vi phạm hoặc không (không có giới hạn ràng buộc). Có thể thấy, tập các cách chia vi phạm ít nhất một trong các điều kiện là hợp của các ; nói cách khác, ta cần đếm:
Nhờ công thức Chia kẹo Euler có chặn dưới đã được trình bày ở phần trên, ta hoàn toàn có thể tính được số cách chia đồng thời vi phạm cận trên của các người nhận thuộc tập , với mọi . Nói một cách toán học hơn, ta cần tính:
Giá trị của được xác định bằng kết quả của bài toán Chia kẹo Euler có chặn dưới với mảng được định nghĩa như sau:
Khi đã tính được các , ta áp dụng bao hàm -- loại trừ để tìm số cách chia có ít nhất một điều kiện bị vi phạm:
Đây chính là số lượng cách chia kẹo không hợp lệ. Để tìm đáp án cuối cùng, ta lấy trừ đi kết quả vừa tính được. Cuối cùng, ta có công thức xác định đáp án như sau:
Như vậy, chỉ cần tính các giao theo công thức chia kẹo Euler rồi áp dụng bao hàm–loại trừ là ta có thể giải được bài toán kể cả khi có tới điều kiện cùng lúc.
Cài đặt
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
// Hàm tính C(n, k) (số cách chọn k từ n)
ll C(ll n, ll k) {
if(k < 0 || k > n) return 0;
ll res = 1;
for(ll i = 1; i <= k; i++) {
res = res * (n - i + 1) / i;
}
return res;
}
// Hàm tính số cách chia m viên kẹo cho n người với cận dưới L[]
ll eulerWays(ll m, int n, vector<int> &L) {
ll sumL = accumulate(L.begin(), L.end(), 0LL);
m -= sumL;
if(m < 0) return 0;
return C(m + n - 1, n - 1);
}
int main() {
int K; // số người
ll M; // tổng số kẹo
cin >> K >> M;
vector<int> L(K), U(K);
for(int i = 0; i < K; i++) cin >> L[i]; // cận dưới
for(int i = 0; i < K; i++) cin >> U[i]; // cận trên
// Tính tổng số cách chia tự do (chỉ cận dưới)
ll total = eulerWays(M, K, L);
// Bao hàm–loại trừ để trừ các trường hợp vi phạm cận trên
ll bad = 0;
for(int mask = 1; mask < (1 << K); mask++) {
vector<int> Lmod = L;
int bits = __builtin_popcount(mask);
ll subtract = 0;
for(int i = 0; i < K; i++) {
if(mask & (1 << i)) {
// Nếu i-th người vi phạm, ta đặt xi > Ui => xi >= Ui+1
Lmod[i] = U[i] + 1;
}
}
ll ways = eulerWays(M, K, Lmod);
if(bits % 2 == 1) bad += ways;
else bad -= ways;
}
ll answer = total - bad;
cout << answer << endl;
return 0;
}
¶ Bao hàm loại trừ trên các tính chất đồng nhất
Mở rộng từ ví dụ ở phần trước, thay vì mỗi người có một cận trên riêng , ta xét trường hợp đồng nhất với một cận trên chung . Nói cách khác, bài toán trở thành: Đếm số cách chia viên kẹo cho người sao cho mỗi người nhận tối đa viên kẹo.
Ý tưởng xử lý tương tự như trước, nhưng có một nhận xét quan trọng: các tập là đồng nhất, nên kích thước của giao chỉ phụ thuộc vào số lượng phần tử của , tức , chứ không phụ thuộc vào các chỉ số cụ thể trong .
Do đó, với mỗi (với ), nếu tính được cho một tập bất kỳ có phần tử, ta có thể nhân kết quả với (tức số cách chọn tập có kích thước ) để tính tổng .
Cuối cùng, ta thay đổi công thức bao hàm loại trừ ở trên để có đáp án cho bài toán mới:
Với là một tập bất kỳ có kích thước là , nói cách khác, ta giải bài toán Chia kẹo Euler có chặn dưới với
Có thể thấy, phương pháp này cho phép giải được bài toán ngay cả khi lớn (ví dụ ), vì ta không cần duyệt tất cả tập con mà chỉ duyệt giá trị .
¶ Bao hàm loại trừ trên số nguyên tố
Một ứng dụng quan trọng khác của bao hàm loại trừ đó là thao tác trên tập các thừa số nguyên tố. Khi này, ta xem một số nguyên là một tập hợp với các phần tử là các thừa số nguyên tố của nó. Với các tính chất số học, ta dễ dàng chứng minh kích thước của các tập hợp như vậy là tương đối nhỏ.
¶ Bài toán
Để hiểu rõ hơn về cách hoạt động của mô hình bao hàm loại trừ trên số nguyên tố, ta cùng tìm hiểu bài toán sau đây:
Cho dãy gồm phần tử và truy vấn có dạng:
- Cho một số nguyên , đếm số phần tử thuộc mảng không nguyên tố cùng nhau với . Nói cách khác, đếm số giá trị thỏa .
Giới hạn:
- .
- .
¶ Phân tích
Nhắc lại, để tính ước chung lớn nhất của hai số nguyên, ta tìm tập thừa số nguyên tố của cả hai số (có xét phần tử trùng) rồi lấy giao của hai tập. Để tính ước chung lớn nhất của nhiều số nguyên, ta cũng tìm tập thừa số nguyên tố của mỗi số rồi lấy giao của tất cả các tập.
Với bài toán này, do chỉ cần xét ước chung lớn nhất lớn hơn hay bằng , ta có thể không quan tâm số mũ của thừa số nguyên tố. Nói cách khác, ta bỏ qua các phần tử trùng trong phân tích thừa số nguyên tố của một số bất kỳ.
Ví dụ, số có tập thừa số nguyên tố là , số có tập thừa số nguyên tố là . Ta biết rằng có tập thừa số nguyên tố là nên hiển nhiên lớn hơn . Trường hợp ước chung lớn nhất bằng xảy ra khi tập thừa số nguyên tố là rỗng.
¶ Xây dựng mô hình Bao hàm loại trừ
Từ phân tích trên, dễ thấy hai số không nguyên tố cùng nhau khi và chỉ khi tập thừa số nguyên tố của chúng có ít nhất một phần tử chung. Nói cách khác, với một số nguyên có tập thừa số nguyên tố , một số nguyên không nguyên tố cùng nhau với khi là bội của ít nhất một giá trị .
Gọi là tập các số nguyên thuộc dãy là bội của (với là một số nguyên tố). Dễ thấy, một truy vấn với số nguyên bây giờ tương đương với việc tính giá trị:
Mặt khác, ta có thể dễ dàng đếm số phần tử là bội của toàn bộ giá trị của một tập thừa số nguyên tố nào đó, ta chỉ đơn giản là đếm số bội của tích của tập số. Nói cách khác, ta dễ dàng có giá trị sau với mọi tập thừa số nguyên tố :
Dễ thấy, ta chỉ cần xét các tập có tích không quá vì các tập còn lại hiển nhiên sẽ có giá trị .
Áp dụng Bao hàm loại trừ, ta có thể tính dựa trên :
Như vậy, nếu biết trước các giá trị , ta hoàn toàn có thể tính trong với là số lượng thừa số nguyên tố phân biệt của . Ta có thể chứng minh được rằng giá trị của không thể vượt quá !
Chứng minh
Ta xét số nguyên tố nhỏ nhất:
Trong khi đó , ta thấy rằng không thể tồn tại một số nguyên không quá có nhiều hơn số nguyên tố phân biệt.
Như vậy, nếu tồn tại đáp án, ta chỉ cần chọn một phần tử rồi chọn thêm tối đa phần tử khác để "loại bỏ" ước nguyên tố của phần tử đầu tiên ra khỏi ước chung lớn nhất.
Như vậy, số thao tác duyệt cho mỗi truy vấn là không quá lần.
¶ Tính
Nhiệm vụ còn lại của bài toán là tính một cách hiệu quả. Ta có hai cách làm đều có độ phức tạp phù hợp với bài toán đang xét như sau:
- Duyệt tất cả các tập rồi duyệt tất cả các bội của tích của tập không quá . Độ phức tạp của cách này là được tính bởi chuỗi điều hòa.
- Ta duyệt các phần tử của mảng rồi duyệt các tập con của . Độ phức tạp của cách này là đã được chứng minh ở phần trên.
¶ Cài đặt
Cài đặt
Đầu tiên, ta chuẩn bị hàm preProcess để thực hiện các tiền xử lý như Sàng nguyên tố và chuẩn bị hàm (được lưu ở mảng countMultiple):
const int maxN = 1e5 + 5;
const int maxA = 1e6 + 6;
int A[maxN], countMultiple[maxA], freq[maxA], sieve[maxA], N;
void preProcess() {
// Sàng nguyên tố
iota(sieve, sieve + maxA, 0);
for (int p = 2; p * p < maxA; p++) {
if (sieve[p] < p) continue;
for (int a = p * p; a < maxA; a += p) sieve[a] = p;
}
// Chuẩn bị mảng countMultiple[S]
for (int i = 0; i < N; i++) freq[A[i]]++;
for (int p = 1; p < maxA; p++)
for (int mult = p; mult < maxA; mult += p) countMultiple[p] += freq[mult];
}
Sau đó, ta cài đặt hàm truy vấn như sau:
int query (int x) {
// Phân tích thừa số nguyên tố và giữ lại tập thừa số phân biệt
vector<int> vec;
while (x > 1) {
int curPrime = sieve[x];
vec.push_back(curPrime);
while (x % curPrime == 0) x /= curPrime;
}
// Tìm bội của từng tập con và thực hiện Bao hàm loại trừ
vector<int> multiple(1 << vec.size(), 1);
int ans = 0;
for (int mask = 1; mask < (1 << vec.size()); mask++) {
int cur = __builtin_ctz(mask);
multiple[mask] = multiple[mask ^ (1 << cur)] * vec[cur];
if (__builtin_parity(mask))
ans += countMultiple[multiple[mask]];
else ans -= countMultiple[multiple[mask]];
}
return ans;
}
¶ Các bài tập áp dụng
¶ HDUOJ - Co-prime
Cho , bạn cần tính số lượng số nguyên trong đoạn sao cho nguyên tố cùng nhau với , tức là .
Có bộ test.
Giới hạn:
- .
- .
¶ Phân tích
Để ý rằng, nếu chúng ta có thể tính số lượng số nguyên trong đoạn sao cho nguyên tố cùng nhau với , ký hiệu là , thì đáp án cho bài toán sẽ là:
Vậy làm thế nào để tính ? Một số không nguyên tố cùng nhau với khi và chỉ khi tồn tại thừa số nguyên tố của sao cho chia hết cho . Vì vậy, thay vì đếm số lượng các số nguyên tố cùng nhau với , ta có thể đếm số lượng các số không nguyên tố cùng nhau với , tức là các số chia sẻ ít nhất một thừa số nguyên tố với .
Như vậy ta gọi là tập hợp các số chia hết cho .
Lúc này, bài toán trở thành tính:
Việc tính hợp này có thể hơi khó, nhưng nhờ Nguyên lý Bao hàm – Loại trừ có giới hạn, ta có thể chuyển bài toán về tính kích thước của các giao, vốn đơn giản hơn.
Cài đặt
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
// Thừa số nguyên tố phân biệt của n
vector<long long> facd(long long n) {
vector<long long> p;
if (n % 2 == 0) {
p.push_back(2);
while (n % 2 == 0) n /= 2;
}
for (long long i = 3; i * i <= n; i += 2) {
if (n % i == 0) {
p.push_back(i);
while (n % i == 0) n /= i;
}
}
if (n > 1) p.push_back(n);
return p;
}
// Đếm số không cùng nhau trong [1..x]
long long cntn(long long x, const vector<long long>& p) {
if (x <= 0) return 0;
int k = p.size(); long long s = 0, tot = 1 << k;
for (int m = 1; m < tot; ++m) {
long long pr = 1; int b = 0; bool ov = 0;
for (int i = 0; i < k; ++i) if (m & (1 << i)) {
++b;
if (pr > x / p[i]) { ov = 1; break; }
pr *= p[i];
}
if (ov) continue;
long long c = x / pr;
s += (b % 2 ? c : -c);
}
return s;
}
// Đếm số cùng nhau trong [1..x]
long long cntc(long long x, const vector<long long>& p) {
return x <= 0 ? 0 : x - cntn(x, p);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int T; cin >> T;
for (int t = 0; t < T; ++t) {
long long a, b, n; cin >> a >> b >> n;
vector<long long> p = facd(n);
long long ans = cntc(b, p) - cntc(a - 1, p);
cout << "Case #" << t + 1 << ": " << ans << '\n';
}
return 0;
}
¶ Đánh giá
Độ phức tạp: với là số lượng thừa số nguyên tố phân biệt của .
¶ HDUOJ - Character Encoding
Cho ba số nguyên , yêu cầu tính số nghiệm của hệ phương trình thỏa mãn . In đáp án modulo
Giới hạn:
- Đây là bài tập multi-testcase có , đảm bảo tổng ở các testcase là không quá .
¶ Phân tích
Ta biết rằng số nghiệm nguyên không âm của: được tính công thức chia kẹo euler . Vậy điều duy nhất cần xử lý là loại bỏ ràng buộc . Để làm điều đó, ta áp dụng Nguyên lý Bao hàm – Loại trừ.
Gọi , trong đó là Iverson bracket.
Với mỗi dãy , ta định nghĩa:
- là số dãy sao cho
- là số dãy số sao cho
Khi là tập rỗng, ta không áp đặt điều kiện nào, nên chính là tổng số cách hợp lệ cần tìm. Rõ ràng thấy tập các tính chất này là đồng nhất.
Không mất tính tổng quát, ta xét tập với . Khi đó, hệ điều kiện tương ứng với là:
các biến còn lại không có ràng buộc.
Ta đặt:
Hệ này tương đương với: . Số nghiệm nguyên không âm của hệ trên là:
Áp dụng Nguyên lý Bao hàm – Loại trừ, từ quan hệ:
Từ đó suy ra:
Do chỉ phụ thuộc vào , công thức cuối cùng của ta là:
Cài đặt
#include <bits/stdc++.h>
using namespace std;
const long long MOD = 998244353LL;
// lũy thừa nhị phân mod MOD
long long pw(long long a, long long e) {
long long r = 1 % MOD; a %= MOD;
while (e) {
if (e & 1) r = r * a % MOD;
a = a * a % MOD;
e >>= 1;
}
return r;
}
// tiền xử lý giai thừa và nghịch đảo giai thừa
void prep(int n, vector<long long>& f, vector<long long>& inv) {
f.assign(n + 1, 1);
inv.assign(n + 1, 1);
for (int i = 1; i <= n; ++i) f[i] = f[i - 1] * i % MOD;
inv[n] = pw(f[n], MOD - 2);
for (int i = n; i >= 1; --i) inv[i - 1] = inv[i] * i % MOD;
}
// C(n, r) mod MOD
long long C(int n, int r, const vector<long long>& f, const vector<long long>& inv) {
if (r < 0 || r > n) return 0;
return f[n] * inv[r] % MOD * inv[n - r] % MOD;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
vector<int> n(T), m(T), k(T);
int mx = 0;
for (int i = 0; i < T; ++i) {
cin >> n[i] >> m[i] >> k[i];
mx = max(mx, k[i] + m[i]);
}
vector<long long> f, inv;
prep(mx, f, inv);
for (int t = 0; t < T; ++t) {
int N = n[t], M = m[t], K = k[t];
if (1LL * M * (N - 1) < K) {
cout << 0 << '\n';
continue;
}
long long ans = 0;
int J = min(M, K / N);
for (int j = 0; j <= J; ++j) {
long long w1 = C(M, j, f, inv);
long long w2 = C(K - j * N + M - 1, M - 1, f, inv);
long long cur = w1 * w2 % MOD;
if (j & 1) ans = (ans - cur + MOD) % MOD;
else ans = (ans + cur) % MOD;
}
cout << ans << '\n';
}
return 0;
}
¶ Đánh giá
Độ phức tạp của thuật toán trên là , do chỉ cần tiền xử lý giai thừa và nghịch đảo modulo của giai thừa.
¶ Codeforces Round 519 - Make It One
Cho dãy số nguyên dương . Tìm một dãy con (không nhất thiết liên tiếp) gồm ít phần tử nhất sao cho ước chung lớn nhất của dãy này có giá trị là . Nếu không tồn tại thì in ra .
Giới hạn:
- .
- .
¶ Phân tích
Đầu tiên ta có nhận xét rằng số phần tử cần chọn không vượt quá .
Chứng minh
Tương tự ví dụ ở phần trước, ta xét số nguyên tố nhỏ nhất:
Trong khi đó , ta thấy rằng không thể tồn tại một số nguyên không quá có nhiều hơn số nguyên tố phân biệt.
Như vậy, nếu tồn tại đáp án, ta chỉ cần chọn một phần tử rồi chọn thêm tối đa phần tử khác để "loại bỏ" ước nguyên tố của phần tử đầu tiên ra khỏi ước chung lớn nhất.
Từ đó, ta định nghĩa:
- là số cách chọn dãy con gồm phần tử sao cho ước chung lớn nhất của chúng có giá trị là .
- là số phần tử sao cho |
Chúng ta có thể áp dụng Nguyên lý Bao Hàm - Loại trừ để chuyển trạng thái quy hoạch động. Số cách chọn dãy con gồm phần tử mà cả phần tử đều chia hết cho là:
Ta thấy rằng khi các phần tử của một dãy đều chia hết cho , ước chung lớn nhất của chúng cũng phải chia hết cho . Nói cách khác, các dãy trong số dãy mà ta đang xét bao gồm các dãy có ước chung lớn nhất là , , ,... Để giữ lại các dãy có ước chung lớn nhất là đúng , ta sử dụng bao hàm - loại trừ:
Chỉ cần xét với . Cách duyệt này có độ phức tạp theo chuỗi điều hòa.
Cuối cùng, ta xét hai trường hợp cho đáp án của bài toán:
- Nếu với mọi thì kết quả là .
- Ngược lại, đáp án là nhỏ nhất sao cho
Độ phức tạp: với .
Cài đặt
#include <bits/stdc++.h>
using namespace std;
static const int MAXA = 300000;
static const int MOD = 1000000007;
long long pw(long long a, long long e)
{
long long r = 1;
while (e)
{
if (e & 1) r = r * a % MOD;
a = a * a % MOD;
e >>= 1;
}
return r;
}
long long C(int n, int k)
{
if (n < k || k < 0) return 0;
static long long fact[MAXA + 1], invfact[MAXA + 1];
static bool built = false;
if (!built)
{
fact[0] = 1;
for (int i = 1; i <= MAXA; i++) fact[i] = fact[i - 1] * i % MOD;
invfact[MAXA] = pw(fact[MAXA], MOD - 2);
for (int i = MAXA; i > 0; i--) invfact[i - 1] = invfact[i] * i % MOD;
built = true;
}
return fact[n] * invfact[k] % MOD * invfact[n - k] % MOD;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
vector<int> freq(MAXA + 1, 0);
for (int x : a) freq[x]++;
vector<int> cnt(MAXA + 1, 0);
for (int i = 1; i <= MAXA; i++)
for (int j = i; j <= MAXA; j += i)
cnt[i] += freq[j];
static long long dp[8][MAXA + 1];
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= 7; i++)
{
for (int j = MAXA; j >= 1; j--)
{
long long val = C(cnt[j], i);
for (int k = 2; k * j <= MAXA; k++)
val = (val - dp[i][k * j] + MOD) % MOD;
dp[i][j] = val;
}
if (dp[i][1] > 0)
{
cout << i;
return 0;
}
}
cout << -1;
return 0;
}
¶ Phụ lục
¶ Luyện tập thêm
- SPOJ - Another Game With Numbers
- SPOJ - Sky Code
- SPOJ - Square-free integers
- SPOJ - Almost Prime Numbers Again
- SPOJ - Find number of Pair of Friends
- SPOJ - Balanced Cow Subsets
- Educational Codeforces Round 20 - Coprime Subsequence
- Educational Codeforces Round 45 - GCD Counting
- Codeforces Round 534 - Professional Layer
- JOI 2018 - Snake Escaping
- CSES - Counting Reorders
- CSES - Counting Coprime Pairs