Tác giả: Phan Đình Khôi - Đại học Bách Khoa Đà Nẵng
Reviewer: Nguyễn Khánh
Bài viết này sẽ giúp bạn tìm hiểu thêm về kỹ thuật hai con trỏ . Kỹ thuật này được sử dụng khá phổ biến, giúp chương trình tiết kiệm thời gian và không gian xử lý.
Cho hai dãy số nguyên đã được sắp xếp không giảm a a a b b b n n n m m m c c c không giảm .
Giới hạn: n , m ≤ 1 0 5 n, m \leq 10^5 n , m ≤ 1 0 5 0 ≤ a i , b i ≤ 1 0 9 0 \leq a_i, b_i \leq 10^{9} 0 ≤ a i , b i ≤ 1 0 9
Hãy cùng xem ví dụ sau đây.
Cho trước hai dãy số a a a b b b
a = [ 1 , 3 , 6 , 8 , 10 ] a=[1,3,6,8,10]
a = [ 1 , 3 , 6 , 8 , 10 ]
b = [ 2 , 6 , 7 , 12 , 14 , 15 ] b=[2,6,7,12,14,15]
b = [ 2 , 6 , 7 , 12 , 14 , 15 ]
Làm cách nào để có thể ghép chúng thành một dãy số c c c
Trước tiên, hãy cùng xác định phần tử đầu tiên của dãy c c c
Vì dãy c c c c c c a a a b b b
Ta có thể so sánh hai phần tử nhỏ nhất của hai dãy a a a b b b c c c
Dãy a a a b b b a [ 1 ] a[1] a [ 1 ] b [ 1 ] b[1] b [ 1 ]
a = [ 1 ↓ , 3 , 6 , 8 , 10 ] a=[\overset{\downarrow}{\color{red}1},3,6,8,10]
a = [ 1 ↓ , 3 , 6 , 8 , 10 ]
b = [ 2 ↓ , 6 , 7 , 12 , 14 , 15 ] b=[\overset{\downarrow}{2},6,7,12,14,15]
b = [ 2 ↓ , 6 , 7 , 12 , 14 , 15 ]
c = [ 1 ] c=[{\color{red}1}]
c = [ 1 ]
Bây giờ, phần tử tiếp theo của dãy c c c c c c
Dãy a a a b b b a [ 1 ] a[1] a [ 1 ] c c c a [ 2 ] a[2] a [ 2 ] a a a b [ 1 ] b[1] b [ 1 ] b b b
So sánh a [ 2 ] a[2] a [ 2 ] b [ 1 ] b[1] b [ 1 ] c c c
a = [ 1 , 3 ↓ , 6 , 8 , 10 ] a=[1,\overset{\downarrow}{3},6,8,10]
a = [ 1 , 3 ↓ , 6 , 8 , 10 ]
b = [ 2 ↓ , 6 , 7 , 12 , 14 , 15 ] b=[\overset{\downarrow}{\color{red}2},6,7,12,14,15]
b = [ 2 ↓ , 6 , 7 , 12 , 14 , 15 ]
c = [ 1 , 2 ] c=[1,{\color{red}2}]
c = [ 1 , 2 ]
Sau khi đưa b [ 1 ] b[1] b [ 1 ] c c c b [ 2 ] b[2] b [ 2 ] b b b
Vẫn như thế, phần tử tiếp theo của dãy c c c c c c
So sánh b [ 2 ] b[2] b [ 2 ] a [ 2 ] a[2] a [ 2 ] c c c
a = [ 1 , 3 ↓ , 6 , 8 , 10 ] a=[1,\overset{\downarrow}{\color{red}3},6,8,10]
a = [ 1 , 3 ↓ , 6 , 8 , 10 ]
b = [ 2 , 6 ↓ , 7 , 12 , 14 , 15 ] b=[2,\overset{\downarrow}{6},7,12,14,15]
b = [ 2 , 6 ↓ , 7 , 12 , 14 , 15 ]
c = [ 1 , 2 , 3 ] c=[1,2,{\color{red}3}]
c = [ 1 , 2 , 3 ]
Sau khi đưa a [ 2 ] a[2] a [ 2 ] c c c a [ 3 ] a[3] a [ 3 ] a a a
Ta nhận thấy rằng
Tại mọi thời điểm, phần tử tiếp theo được đưa vào dãy c c c
Bằng cách so sánh phần tử nhỏ nhất chưa được chọn ở dãy a a a b b b c c c
Ban đầu, lúc dãy c c c
a [ 1 ] a[1] a [ 1 ] a a a b [ 1 ] b[1] b [ 1 ] b b b
Khi đưa phần tử a [ i ] a[i] a [ i ] c c c a a a a [ i + 1 ] a[i+1] a [ i + 1 ]
Khi đưa phần tử b [ j ] b[j] b [ j ] c c c b b b b [ j + 1 ] b[j+1] b [ j + 1 ]
Dựa vào những phân tích ta có giải pháp sử dụng hai con trỏ như sau:
Dãy a a a i i i a a a
Con trỏ i i i a a a
Dãy b b b j j j b b b
Con trỏ j j j b b b
Ta sẽ lặp lại công việc này, cho đến khi đưa hết các phần tử trong dãy a a a b b b c c c
Khi các phần tử trong một dãy nào đó, dãy a a a b b b c c c c c c
Ngược lại:
So sánh hai phần tử ở hai con trỏ.
Đưa phần tử có giá trị nhỏ hơn vào dãy c c c
Tăng vị trí con trỏ ở phần tử được đưa vào lên một đơn vị.
Để hiểu rõ hơn, ta hãy cùng xem qua ví dụ sau đây:
a = [ 1 , 3 , 6 , 8 , 10 ] , b = [ 2 , 6 , 7 , 12 , 14 , 15 ] a = [1, 3, 6, 8, 10], b = [2, 6, 7, 12, 14,15] a = [ 1 , 3 , 6 , 8 , 10 ] , b = [ 2 , 6 , 7 , 12 , 14 , 15 ]
Đặt i = 1 i = 1 i = 1 j = 1 j = 1 j = 1 a = [ 1 i ↓ , 3 , 6 , 8 , 10 ] a = [\overset{\underset{\downarrow}{\color{red}i}}{\color{red}1}, 3, 6, 8, 10] a = [ 1 ↓ i , 3 , 6 , 8 , 10 ] b = [ 2 j ↑ , 6 , 7 , 12 , 14 , 15 ] b = [\underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}2}, 6, 7, 12, 14,15] b = [ j ↑ 2 , 6 , 7 , 12 , 14 , 15 ] c = [ ] c = [] c = [ ]
Vì a [ i ] < b [ j ] a[i]<b[j] a [ i ] < b [ j ] a [ i ] a[i] a [ i ] c c c i i i a = [ 1 , 3 i ↓ , 6 , 8 , 10 ] a = [1,\overset{\underset{\downarrow}{\color{red}i}}{\color{red}3}, 6, 8, 10] a = [ 1 , 3 ↓ i , 6 , 8 , 10 ] b = [ 2 j ↑ , 6 , 7 , 12 , 14 , 15 ] b = [\underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}2}, 6, 7, 12, 14,15] b = [ j ↑ 2 , 6 , 7 , 12 , 14 , 15 ] c = [ 1 ] c = [1] c = [ 1 ]
Vì b [ j ] < a [ i ] b[j]<a[i] b [ j ] < a [ i ] b [ j ] b[j] b [ j ] c c c j j j a = [ 1 , 3 i ↓ , 6 , 8 , 10 ] a = [1, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}3}, 6, 8, 10] a = [ 1 , 3 ↓ i , 6 , 8 , 10 ] b = [ 2 , 6 j ↑ , 7 , 12 , 14 , 15 ] b = [2, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}6}, 7, 12, 14,15] b = [ 2 , j ↑ 6 , 7 , 12 , 14 , 15 ] c = [ 1 , 2 ] c = [1, 2] c = [ 1 , 2 ]
Vì a [ i ] < b [ j ] a[i]<b[j] a [ i ] < b [ j ] a [ i ] a[i] a [ i ] c c c i i i a = [ 1 , 3 , 6 i ↓ , 8 , 10 ] a = [1, 3, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}6}, 8, 10] a = [ 1 , 3 , 6 ↓ i , 8 , 10 ] b = [ 2 , 6 j ↑ , 7 , 12 , 14 , 15 ] b = [2, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}6}, 7, 12, 14,15] b = [ 2 , j ↑ 6 , 7 , 12 , 14 , 15 ] c = [ 1 , 2 , 3 ] c = [1, 2, 3] c = [ 1 , 2 , 3 ]
Vì a [ i ] = b [ j ] a[i]=b[j] a [ i ] = b [ j ] a [ i ] a[i] a [ i ] c c c i i i a = [ 1 , 3 , 6 , 8 i ↓ , 10 ] a = [1, 3, 6, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}8}, 10] a = [ 1 , 3 , 6 , 8 ↓ i , 10 ] b = [ 2 , 6 j ↑ , 7 , 12 , 14 , 15 ] b = [2, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}6}, 7, 12, 14,15] b = [ 2 , j ↑ 6 , 7 , 12 , 14 , 15 ] c = [ 1 , 2 , 3 , 6 ] c = [1, 2, 3, 6] c = [ 1 , 2 , 3 , 6 ]
Vì b [ j ] < a [ i ] b[j]<a[i] b [ j ] < a [ i ] b [ j ] b[j] b [ j ] c c c j j j a = [ 1 , 3 , 6 , 8 i ↓ , 10 ] a = [1, 3, 6, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}8}, 10] a = [ 1 , 3 , 6 , 8 ↓ i , 10 ] b = [ 2 , 6 , 7 j ↑ , 12 , 14 , 15 ] b = [2, 6, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}7}, 12, 14,15] b = [ 2 , 6 , j ↑ 7 , 12 , 14 , 15 ] c = [ 1 , 2 , 3 , 6 , 6 ] c = [1, 2, 3, 6, 6] c = [ 1 , 2 , 3 , 6 , 6 ]
Vì b [ j ] < a [ i ] b[j]<a[i] b [ j ] < a [ i ] b [ j ] b[j] b [ j ] c c c j j j a = [ 1 , 3 , 6 , 8 i ↓ , 10 ] a = [1, 3, 6, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}8}, 10] a = [ 1 , 3 , 6 , 8 ↓ i , 10 ] b = [ 2 , 6 , 7 , 12 j ↑ , 14 , 15 ] b = [2, 6, 7, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 14,15] b = [ 2 , 6 , 7 , j ↑ 12 , 14 , 15 ] c = [ 1 , 2 , 3 , 6 , 6 , 7 ] c = [1, 2, 3, 6, 6, 7] c = [ 1 , 2 , 3 , 6 , 6 , 7 ]
Vì a [ i ] < b [ j ] a[i]<b[j] a [ i ] < b [ j ] a [ i ] a[i] a [ i ] c c c i i i a = [ 1 , 3 , 6 , 8 , 10 i ↓ ] a = [1, 3, 6, 8, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}10}] a = [ 1 , 3 , 6 , 8 , 10 ↓ i ] b = [ 2 , 6 , 7 , 12 j ↑ , 14 , 15 ] b = [2, 6, 7, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 14,15] b = [ 2 , 6 , 7 , j ↑ 12 , 14 , 15 ] c = [ 1 , 2 , 3 , 6 , 6 , 7 , 8 ] c = [1, 2, 3, 6, 6, 7, 8] c = [ 1 , 2 , 3 , 6 , 6 , 7 , 8 ]
Vì a [ i ] < b [ j ] a[i]<b[j] a [ i ] < b [ j ] a [ i ] a[i] a [ i ] c c c i i i a = [ 1 , 3 , 6 , 8 , 10 ] i ↓ a = [1, 3, 6, 8, 10]\overset{\underset{\downarrow}{\color{red}i}}{ } a = [ 1 , 3 , 6 , 8 , 10 ] ↓ i b = [ 2 , 6 , 7 , 12 j ↑ , 14 , 15 ] b = [2, 6, 7, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 14,15] b = [ 2 , 6 , 7 , j ↑ 12 , 14 , 15 ] c = [ 1 , 2 , 3 , 6 , 6 , 7 , 8 , 10 ] c = [1, 2, 3, 6, 6, 7, 8, 10] c = [ 1 , 2 , 3 , 6 , 6 , 7 , 8 , 10 ]
Vì tất cả các phần tử trong dãy a a a c c c b b b c c c c = [ 1 , 2 , 3 , 6 , 6 , 7 , 8 , 10 , 12 , 14 , 15 ] c = [1, 2, 3, 6, 6, 7, 8, 10, 12, 14,15] c = [ 1 , 2 , 3 , 6 , 6 , 7 , 8 , 10 , 12 , 14 , 15 ]
Cài đặt
int i = 1, j = 1;
vector<int> c;
while (i <= n || j <= m){
if (j == m + 1 || (i <= n && a[i] <= b[j]))
c.push_back(a[i++]);
else
c.push_back(b[j++]);
}
for (auto it: c)
cout << it << " ";
Độ phức tạp
Vị trí con trỏ i i i n n n j j j m m m
Vì thế độ phức tạp của giải pháp là O ( n + m ) O(n+m) O ( n + m )
Cho một mảng số nguyên a a a n n n sắp xếp tăng dần . Hãy tìm hai vị trí khác nhau bất kỳ sao cho tổng của hai phần tử ở hai vị trí đó có giá trị là x x x
Giới hạn: 2 ≤ n ≤ 1 0 6 2 \leq n \leq 10^6 2 ≤ n ≤ 1 0 6 0 ≤ a i , x ≤ 1 0 9 0 \leq a_i, x \leq 10^9 0 ≤ a i , x ≤ 1 0 9
Hãy cùng xem ví dụ sau đây.
Cho trước mảng số a a a x = 16 x=16 x = 16
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ] a=[2,5,6,8,10,12,15]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ]
Làm cách nào để có thể tìm hai vị trí khác nhau mà tổng hai phần tử ở hai vị trí đó có tổng là x x x
Trước tiên, ta có một chút nhận xét sau:
a [ 1 ] < a [ 2 ] < a [ 3 ] < a [ 4 ] < a [ 5 ] < a [ 6 ] < a [ 7 ] a[1]<a[2]<a[3]<a[4]<a[5]<a[6]<a[7] a [ 1 ] < a [ 2 ] < a [ 3 ] < a [ 4 ] < a [ 5 ] < a [ 6 ] < a [ 7 ] a a a a [ 1 ] + a [ 7 ] = 17 > X ⇒ X < a [ 1 ] + a [ 7 ] < a [ 2 ] + a [ 7 ] < a [ 3 ] + a [ 7 ] < a [ 4 ] + a [ 7 ] < a [ 5 ] + a [ 7 ] < a [ 6 ] + a [ 7 ] a[1]+a[7]=17>X \Rightarrow X<a[1]+a[7]<a[2]+a[7]<a[3]+a[7]<a[4]+a[7]<a[5]+a[7]<a[6]+a[7] a [ 1 ] + a [ 7 ] = 17 > X ⇒ X < a [ 1 ] + a [ 7 ] < a [ 2 ] + a [ 7 ] < a [ 3 ] + a [ 7 ] < a [ 4 ] + a [ 7 ] < a [ 5 ] + a [ 7 ] < a [ 6 ] + a [ 7 ]
Có thể thấy, tổng của a [ 7 ] a[7] a [ 7 ] X X X a [ 7 ] a[7] a [ 7 ]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ] a=[2,5,6,8,10,12,{\color{red}15}]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ]
a [ 1 ] + a [ 6 ] = 14 < X ⇒ a [ 1 ] + a [ 2 ] < a [ 1 ] + a [ 3 ] < a [ 1 ] + a [ 4 ] < a [ 1 ] + a [ 5 ] < a [ 1 ] + a [ 6 ] < X a[1]+a[6]=14<X \Rightarrow a[1]+a[2]<a[1]+a[3]<a[1]+a[4]<a[1]+a[5]<a[1]+a[6]<X a [ 1 ] + a [ 6 ] = 14 < X ⇒ a [ 1 ] + a [ 2 ] < a [ 1 ] + a [ 3 ] < a [ 1 ] + a [ 4 ] < a [ 1 ] + a [ 5 ] < a [ 1 ] + a [ 6 ] < X
Có thể thấy, tổng của a [ 1 ] a[1] a [ 1 ] x x x a [ 1 ] a[1] a [ 1 ]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ] a=[{\color{red}2},5,6,8,10,12,{\color{red}15}]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ]
a [ 2 ] + a [ 6 ] = 17 > X ⇒ X < a [ 2 ] + a [ 6 ] < a [ 3 ] + a [ 6 ] < a [ 4 ] + a [ 6 ] < a [ 5 ] + a [ 6 ] a[2]+a[6]=17>X \Rightarrow X<a[2]+a[6]<a[3]+a[6]<a[4]+a[6]<a[5]+a[6] a [ 2 ] + a [ 6 ] = 17 > X ⇒ X < a [ 2 ] + a [ 6 ] < a [ 3 ] + a [ 6 ] < a [ 4 ] + a [ 6 ] < a [ 5 ] + a [ 6 ]
Có thể thấy, tổng của a [ 6 ] a[6] a [ 6 ] x x x a [ 6 ] a[6] a [ 6 ]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ] a=[{\color{red}2},5,6,8,10,{\color{red}12},{\color{red}15}]
a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ]
Như vậy, tại một thời điểm bất kỳ, những phần tử chúng ta cần quan tâm đến sẽ là các phần tử trong đoạn [ i , j ] [i,j] [ i , j ]
Ta có một số nhận xét sau:
Nếu i = j i=j i = j A A A X X X
Ngược lại:
Nếu a [ i ] + a [ j ] = X a[i]+a[j]=X a [ i ] + a [ j ] = X i i i j j j
Nếu a [ i ] + a [ j ] < X a[i]+a[j]<X a [ i ] + a [ j ] < X a [ i ] a[i] a [ i ] [ i + 1 , j ] [i+1,j] [ i + 1 , j ]
Nếu a [ i ] + a [ j ] > X a[i]+a[j]>X a [ i ] + a [ j ] > X a [ j ] a[j] a [ j ] [ i , j − 1 ] [i,j-1] [ i , j − 1 ]
Từ những phân tích vừa rồi ta có giải pháp sử dụng hai con trỏ như sau:
Một con trỏ ( i ) (i) ( i ) A A A ( j ) (j) ( j ) A A A
Nếu tổng của hai phần tử ở hai vị trí con trỏ
Nhỏ hơn X X X i i i
Lớn hơn X X X j j j
Tiếp tục di chuyển cho đến khi hai con trỏ gặp nhau.
Khi con trỏ chưa gặp nhau mà tổng ở hai vị trí con trỏ có giá trị là X X X i i i j j j
Để hiểu rõ hơn, ta hãy cùng xem qua một số ví dụ sau đây:
Ví dụ 1: a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ] a = [2, 5, 6, 8, 10, 12, 15] a = [ 2 , 5 , 6 , 8 , 10 , 12 , 15 ] x = 16 x = 16 x = 16
Đặt i = 1 i=1 i = 1 j = N j=N j = N a = [ 2 i ↓ , 5 , 6 , 8 , 10 , 12 , 15 j ↑ ] a = [\overset{\underset{\downarrow}{\color{red}i}}{\color{red}2}, 5, 6, 8, 10, 12, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}15}] a = [ 2 ↓ i , 5 , 6 , 8 , 10 , 12 , j ↑ 15 ]
Vì a [ i ] + a [ j ] = 2 + 15 = 17 > x a[i]+a[j]=2+15=17>x a [ i ] + a [ j ] = 2 + 15 = 17 > x j j j a = [ 2 i ↓ , 5 , 6 , 8 , 10 , 12 j ↑ , 15 ] a = [\overset{\underset{\downarrow}{\color{red}i}}{\color{red}2}, 5, 6, 8, 10, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 15] a = [ 2 ↓ i , 5 , 6 , 8 , 10 , j ↑ 12 , 15 ]
Vì a [ i ] + a [ j ] = 2 + 12 = 14 < x a[i]+a[j]=2+12=14<x a [ i ] + a [ j ] = 2 + 12 = 14 < x i i i a = [ 2 , 5 i ↓ , 6 , 8 , 10 , 12 j ↑ , 15 ] a = [2, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}5}, 6, 8, 10, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 15] a = [ 2 , 5 ↓ i , 6 , 8 , 10 , j ↑ 12 , 15 ]
Vì a [ i ] + a [ j ] = 5 + 12 = 17 > x a[i]+a[j]=5+12=17>x a [ i ] + a [ j ] = 5 + 12 = 17 > x j j j a = [ 2 , 5 i ↓ , 6 , 8 , 10 j ↑ , 12 , 15 ] a = [2, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}5}, 6, 8, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}10}, 12, 15] a = [ 2 , 5 ↓ i , 6 , 8 , j ↑ 10 , 12 , 15 ]
Vì a [ i ] + a [ j ] = 5 + 10 < x a[i]+a[j]=5+10<x a [ i ] + a [ j ] = 5 + 10 < x i i i a = [ 2 , 5 , 6 i ↓ , 8 , 10 j ↑ , 12 , 15 ] a = [2, 5, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}6}, 8, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}10}, 12, 15] a = [ 2 , 5 , 6 ↓ i , 8 , j ↑ 10 , 12 , 15 ]
Vì a [ i ] + a [ j ] = 6 + 10 = x a[i]+a[j]=6+10=x a [ i ] + a [ j ] = 6 + 10 = x i i i j j j
Ví dụ 2: a = [ 2 , 3 , 7 , 8 , 10 , 12 , 15 ] a = [2, 3, 7, 8, 10, 12, 15] a = [ 2 , 3 , 7 , 8 , 10 , 12 , 15 ] x = 16 x = 16 x = 16
Đặt i = 1 i=1 i = 1 j = N j=N j = N a = [ 2 i ↓ , 3 , 7 , 8 , 10 , 12 , 15 j ↑ ] a = [\overset{\underset{\downarrow}{\color{red}i}}{\color{red}2}, 3, 7, 8, 10, 12, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}15}] a = [ 2 ↓ i , 3 , 7 , 8 , 10 , 12 , j ↑ 15 ]
Vì a [ i ] + a [ j ] = 5 + 12 = 17 > x a[i]+a[j]=5+12=17>x a [ i ] + a [ j ] = 5 + 12 = 17 > x j j j a = [ 2 i ↓ , 3 , 7 , 8 , 10 , 12 j ↑ , 15 ] a = [\overset{\underset{\downarrow}{\color{red}i}}{\color{red}2}, 3, 7, 8, 10, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 15] a = [ 2 ↓ i , 3 , 7 , 8 , 10 , j ↑ 12 , 15 ]
Vì a [ i ] + a [ j ] = 2 + 12 = 14 < x a[i]+a[j]=2+12=14<x a [ i ] + a [ j ] = 2 + 12 = 14 < x i i i a = [ 2 , 3 i ↓ , 7 , 8 , 10 , 12 j ↑ , 15 ] a = [2, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}3}, 7, 8, 10, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 15] a = [ 2 , 3 ↓ i , 7 , 8 , 10 , j ↑ 12 , 15 ]
Vì a [ i ] + a [ j ] = 3 + 12 = 15 < x a[i]+a[j]=3+12=15<x a [ i ] + a [ j ] = 3 + 12 = 15 < x i i i a = [ 2 , 3 , 7 i ↓ , 8 , 10 , 12 j ↑ , 15 ] a = [2, 3, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}7}, 8, 10, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}12}, 15] a = [ 2 , 3 , 7 ↓ i , 8 , 10 , j ↑ 12 , 15 ]
Vì a [ i ] + a [ j ] = 7 + 12 = 19 > x a[i]+a[j]=7+12=19>x a [ i ] + a [ j ] = 7 + 12 = 19 > x j j j a = [ 2 , 3 , 7 i ↓ , 8 , 10 j ↑ , 12 , 15 ] a = [2, 3, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}7}, 8, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}10}, 12, 15] a = [ 2 , 3 , 7 ↓ i , 8 , j ↑ 10 , 12 , 15 ]
Vì a [ i ] + a [ j ] = 7 + 10 = 17 > x a[i]+a[j]=7+10=17>x a [ i ] + a [ j ] = 7 + 10 = 17 > x j j j a = [ 2 , 3 , 7 i ↓ , 8 j ↑ , 10 , 12 , 15 ] a = [2, 3, \overset{\underset{\downarrow}{\color{red}i}}{\color{red}7}, \underset{\overset{\uparrow}{\color{blue}j}}{\color{blue}8}, 10, 12, 15] a = [ 2 , 3 , 7 ↓ i , j ↑ 8 , 10 , 12 , 15 ]
Vì a [ i ] + a [ j ] = 7 + 8 = 15 < x a[i]+a[j]=7+8=15<x a [ i ] + a [ j ] = 7 + 8 = 15 < x i i i a = [ 2 , 3 , 7 , 8 j ↑ i ↓ , 10 , 12 , 15 ] a = [2, 3, 7, \overset{\underset{\downarrow}{\color{red}i}}{ \underset{\overset{\uparrow}{\color{blue}j}}{\color{purple}8}}, 10, 12, 15] a = [ 2 , 3 , 7 , j ↑ 8 ↓ i , 10 , 12 , 15 ]
Vì i = j i=j i = j
Cài đặt
int i = 1, j = N;
while (i < j) {
if (a[i] + a[j] == x) {
cout << i << " " << j;
return 0;
}
if (a[i] + a[j] < x)
i += 1;
else
j -= 1;
}
cout << "No solution";
Độ phức tạp
Vị trí con trỏ i i i j j j
Hơn nữa, sự thay đổi vị trí hai con trỏ này sẽ dừng lại khi tổng hai phần tử ở hai vị trí con trỏ có tổng là X X X i i i j j j
Vì thế, việc thay đổi vị trí hai con trỏ sẽ không quá n n n O ( n ) O(n) O ( n )
Cho dãy số nguyên dương a a a n n n s s s
Dữ liệu đảm bảo các phần tử trong dãy a a a s s s
Giới hạn: 1 ≤ n ≤ 1 0 6 1\leq n \leq 10^6 1 ≤ n ≤ 1 0 6 1 ≤ a i ≤ 1 0 9 1 \leq a_i \leq 10^9 1 ≤ a i ≤ 1 0 9 s ≤ 1 0 18 s \leq 10^{18} s ≤ 1 0 18
Để dễ dàng phân tích, ta tạm gọi
s u m ( l , r ) sum(l,r) s u m ( l , r ) [ l , r ] [l,r] [ l , r ] Một đoạn con [ l , r ] [l,r] [ l , r ] s u m ( l , r ) ≤ s sum(l,r) \leq s s u m ( l , r ) ≤ s
Qua đây, bài toán của chúng ta sẽ là tìm độ dài đoạn con "tốt" dài nhất.
Vì dãy a a a
s u m ( 1 , r ) > s u m ( 2 , r ) > . . . > s u m ( r − 1 , r ) > s u m ( r , r ) sum(1,r)>sum(2,r)>...>sum(r-1,r)>sum(r,r) s u m ( 1 , r ) > s u m ( 2 , r ) > ... > s u m ( r − 1 , r ) > s u m ( r , r ) Nếu đoạn con [ l , r ] [l,r] [ l , r ] x ≥ l x\geq l x ≥ l [ x , r ] [x,r] [ x , r ]
Nếu đoạn con [ l , r ] [l,r] [ l , r ] x ≤ l x \leq l x ≤ l [ x , r ] [x,r] [ x , r ]
Với r r r l l l [ l , r ] [l,r] [ l , r ]
mọi x ≥ l x \geq l x ≥ l [ x , r ] [x,r] [ x , r ]
mọi x < l x < l x < l [ x , r ] [x,r] [ x , r ]
đoạn con [ l , r ] [l,r] [ l , r ] r r r
Từ đó, với mỗi r r r 1 1 1 n n n l l l a a a
Hãy cùng nhận xét vị trí của l l l r r r 1 1 1 n n n
Cho trước dãy a = [ 2 , 6 , 5 , 3 , 6 , 8 , 9 ] a = [2, 6, 5, 3, 6, 8, 9] a = [ 2 , 6 , 5 , 3 , 6 , 8 , 9 ] s = 20 s=20 s = 20
r = 1 → l = 1 r=1 \rightarrow l=1 r = 1 → l = 1
a = [ 2 l , r ↓ , 6 , 5 , 3 , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{{\color{red}l},{\color{blue}r}}}{\color{green}2}, 6, 5, 3, 6, 8, 9] a = [ 2 ↓ l , r , 6 , 5 , 3 , 6 , 8 , 9 ] s u m ( l , r ) = 2 sum(l,r)=2 s u m ( l , r ) = 2
r = 2 → l = 1 r=2 \rightarrow l=1 r = 2 → l = 1
a = [ 2 l ↓ , 6 r ↓ , 5 , 3 , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{green}2}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}6}, 5, 3, 6, 8, 9] a = [ 2 ↓ l , 6 ↓ r , 5 , 3 , 6 , 8 , 9 ] s u m ( l , r ) = 8 sum(l,r)=8 s u m ( l , r ) = 8
r = 3 → l = 1 r=3 \rightarrow l=1 r = 3 → l = 1
a = [ 2 l ↓ , 6 , 5 r ↓ , 3 , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{green}2}, {\color{green}6}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}5}, 3, 6, 8, 9] a = [ 2 ↓ l , 6 , 5 ↓ r , 3 , 6 , 8 , 9 ] s u m ( l , r ) = 13 sum(l,r)=13 s u m ( l , r ) = 13
r = 4 → l = 1 r=4 \rightarrow l=1 r = 4 → l = 1
a = [ 2 l ↓ , 6 , 5 , 3 r ↓ , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{green}2}, {\color{green}6}, {\color{green}5}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}3}, 6, 8, 9] a = [ 2 ↓ l , 6 , 5 , 3 ↓ r , 6 , 8 , 9 ] s u m ( l , r ) = 16 sum(l,r)=16 s u m ( l , r ) = 16
r = 5 → l = 2 r=5 \rightarrow l=2 r = 5 → l = 2
a = [ 2 , 6 l ↓ , 5 , 3 , 6 r ↓ , 8 , 9 ] a = [2, \overset{\underset{\downarrow}{\color{red}l}}{\color{green}6}, {\color{green}5}, {\color{green}3}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}6}, 8, 9] a = [ 2 , 6 ↓ l , 5 , 3 , 6 ↓ r , 8 , 9 ] s u m ( l , r ) = 20 sum(l,r)=20 s u m ( l , r ) = 20
r = 6 → l = 4 r=6 \rightarrow l=4 r = 6 → l = 4
a = [ 2 , 6 , 5 , 3 l ↓ , 6 , 8 r ↓ , 9 ] a = [2, 6, 5, \overset{\underset{\downarrow}{\color{red}l}}{\color{green}3}, {\color{green}6}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}8}, 9] a = [ 2 , 6 , 5 , 3 ↓ l , 6 , 8 ↓ r , 9 ] s u m ( l , r ) = 17 sum(l,r)=17 s u m ( l , r ) = 17
r = 7 → l = 6 r=7 \rightarrow l=6 r = 7 → l = 6
a = [ 2 , 6 , 5 , 3 , 6 , 8 l ↓ , 9 r ↓ ] a = [2, 6, 5, 3, 6, \overset{\underset{\downarrow}{\color{red}l}}{\color{green}8}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}9}] a = [ 2 , 6 , 5 , 3 , 6 , 8 ↓ l , 9 ↓ r ] s u m ( l , r ) = 17 sum(l,r)=17 s u m ( l , r ) = 17
r r r l l l Độ dài đoạn con
1 1 1 1 1 1 1 1 1
2 2 2 1 1 1 2 2 2
3 3 3 1 1 1 3 3 3
4 4 4 1 1 1 4 4 4
5 5 5 2 2 2 4 4 4
6 6 6 4 4 4 3 3 3
7 7 7 6 6 6 2 2 2
Độ dài của đoạn con "tốt" dài nhất của dãy là giá trị lớn nhất của độ dài các đoạn con "tốt" dài nhất với vị trí kết thúc từ 1 1 1 n n n
Ở đây, độ dài đoạn con "tốt" dài nhất của dãy là 4 4 4
Qua ví dụ vừa rồi, ta thấy rằng, vị trí l l l r r r 1 1 1 n n n
Thật vậy, với mọi x < l x<l x < l s u m ( x , r ) > s ⇒ s u m ( x , r + 1 ) > s sum(x,r)>s \Rightarrow sum(x,r+1)>s s u m ( x , r ) > s ⇒ s u m ( x , r + 1 ) > s l l l r + 1 r+1 r + 1 l l l r r r
Hơn nữa vì các phần tử trong dãy a a a s s s l ≤ r l \leq r l ≤ r [ l , r ] [l,r] [ l , r ]
Với những phân tích như trên, ta có giải quyết bài toán với phương pháp hai con trỏ như sau:
Hai con trỏ l l l r r r 1 1 1
Hai con trỏ này được thể hiện như hai vị trí l l l r r r
Di chuyển lần lượt con trỏ r r r 1 1 1 n n n
Sau mỗi lần di chuyển con trỏ r r r
s u m ( l , r ) ≤ s sum(l,r) \leq s s u m ( l , r ) ≤ s l l l s u m ( l , r ) > s sum(l,r) > s s u m ( l , r ) > s l l l s u m ( l , r ) ≤ s sum(l,r) \leq s s u m ( l , r ) ≤ s
Hiện tại với vị trí con trỏ l l l r r r r r r [ l , r ] [l,r] [ l , r ]
Độ dài đoạn con "tốt" dài nhất chính là giá trị độ dài lớn nhất của các đoạn "tốt" dài nhất với vị trí kết thúc tại r r r r r r 1 1 1 n n n
Để hiểu rõ hơn, ta hãy cùng xem qua một số ví dụ sau đây:
a = [ 2 , 6 , 5 , 3 , 6 , 8 , 9 ] a = [2, 6, 5, 3, 6, 8, 9] a = [ 2 , 6 , 5 , 3 , 6 , 8 , 9 ] s = 20 s=20 s = 20
Sử dụng biến a n s ans an s r r r r r r 1 1 1 n n n
Đặt l = 1 l=1 l = 1 r = 1 r=1 r = 1
a = [ 2 l , r ↓ , 6 , 5 , 3 , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{{\color{red}l},{\color{blue}r}}}{\color{green}2}, 6, 5, 3, 6, 8, 9] a = [ 2 ↓ l , r , 6 , 5 , 3 , 6 , 8 , 9 ] vì a [ 1 ] ≤ s a[1] \leq s a [ 1 ] ≤ s [ 1 , 1 ] [1,1] [ 1 , 1 ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Tăng vị trí r r r 1 1 1
a = [ 2 l ↓ , 6 r ↓ , 5 , 3 , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{green}2}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}6}, 5, 3, 6, 8, 9] a = [ 2 ↓ l , 6 ↓ r , 5 , 3 , 6 , 8 , 9 ] vì s u m ( l , r ) = 8 ≤ s sum(l,r) = 8 \leq s s u m ( l , r ) = 8 ≤ s [ l , r ] [l,r] [ l , r ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Tăng vị trí r r r 1 1 1
a = [ 2 l ↓ , 6 , 5 r ↓ , 3 , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{green}2}, {\color{green}6}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}5}, 3, 6, 8, 9] a = [ 2 ↓ l , 6 , 5 ↓ r , 3 , 6 , 8 , 9 ] vì s u m ( l , r ) = 13 ≤ s sum(l,r) = 13 \leq s s u m ( l , r ) = 13 ≤ s [ l , r ] [l,r] [ l , r ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Tăng vị trí r r r 1 1 1
a = [ 2 l ↓ , 6 , 5 , 3 r ↓ , 6 , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{green}2}, {\color{green}6}, {\color{green}5}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}3}, 6, 8, 9] a = [ 2 ↓ l , 6 , 5 , 3 ↓ r , 6 , 8 , 9 ] vì s u m ( l , r ) = 16 ≤ s sum(l,r) = 16 \leq s s u m ( l , r ) = 16 ≤ s [ l , r ] [l,r] [ l , r ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Tăng vị trí r r r 1 1 1
a = [ 2 l ↓ , 6 , 5 , 3 , 6 r ↓ , 8 , 9 ] a = [\overset{\underset{\downarrow}{\color{red}l}}{\color{orange}2}, {\color{orange}6}, {\color{orange}5}, {\color{orange}3}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{orange}6}, 8, 9] a = [ 2 ↓ l , 6 , 5 , 3 , 6 ↓ r , 8 , 9 ] vì s u m ( l , r ) = 22 > s sum(l,r) = 22 > s s u m ( l , r ) = 22 > s l l l
Tăng vị trí l l l 1 1 1
a = [ 2 , 6 l ↓ , 5 , 3 , 6 r ↓ , 8 , 9 ] a = [2, \overset{\underset{\downarrow}{\color{red}l}}{\color{green}6}, {\color{green}5}, {\color{green}3}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}6}, 8, 9] a = [ 2 , 6 ↓ l , 5 , 3 , 6 ↓ r , 8 , 9 ] vì s u m ( l , r ) = 20 ≤ s sum(l,r) = 20 \leq s s u m ( l , r ) = 20 ≤ s [ l , r ] [l,r] [ l , r ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Tăng vị trí r r r 1 1 1
a = [ 2 , 6 l ↓ , 5 , 3 , 6 , 8 r ↓ , 9 ] a = [2, \overset{\underset{\downarrow}{\color{red}l}}{\color{orange}6}, {\color{orange}5}, {\color{orange}3}, {\color{orange}6}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{orange}8}, 9] a = [ 2 , 6 ↓ l , 5 , 3 , 6 , 8 ↓ r , 9 ] vì s u m ( l , r ) = 28 > s sum(l,r) = 28 > s s u m ( l , r ) = 28 > s l l l
Tăng vị trí l l l 1 1 1
a = [ 2 , 6 , 5 l ↓ , 3 , 6 , 8 r ↓ , 9 ] a = [2, 6, \overset{\underset{\downarrow}{\color{red}l}}{\color{orange}5}, {\color{orange}3}, {\color{orange}6}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{orange}8}, 9] a = [ 2 , 6 , 5 ↓ l , 3 , 6 , 8 ↓ r , 9 ] vì s u m ( l , r ) = 22 > s sum(l,r) = 22 > s s u m ( l , r ) = 22 > s l l l
Tăng vị trí l l l 1 1 1
a = [ 2 , 6 , 5 , 3 l ↓ , 6 , 8 r ↓ , 9 ] a = [2, 6, 5, \overset{\underset{\downarrow}{\color{red}l}}{\color{green}3}, {\color{green}6}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}8}, 9] a = [ 2 , 6 , 5 , 3 ↓ l , 6 , 8 ↓ r , 9 ] vì s u m ( l , r ) = 17 ≤ s sum(l,r) = 17 \leq s s u m ( l , r ) = 17 ≤ s [ l , r ] [l,r] [ l , r ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Tăng vị trí r r r 1 1 1
a = [ 2 , 6 , 5 , 3 l ↓ , 6 , 8 , 9 r ↓ ] a = [2, 6, 5, \overset{\underset{\downarrow}{\color{red}l}}{\color{orange}3}, {\color{orange}6}, {\color{orange}8}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{orange}9}] a = [ 2 , 6 , 5 , 3 ↓ l , 6 , 8 , 9 ↓ r ] vì s u m ( l , r ) = 26 > s sum(l,r) = 26 > s s u m ( l , r ) = 26 > s l l l
Tăng vị trí l l l 1 1 1
a = [ 2 , 6 , 5 , 3 , 6 l ↓ , 8 , 9 r ↓ ] a = [2, 6, 5, 3, \overset{\underset{\downarrow}{\color{red}l}}{\color{orange}6}, {\color{orange}8}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{orange}9}] a = [ 2 , 6 , 5 , 3 , 6 ↓ l , 8 , 9 ↓ r ] vì s u m ( l , r ) = 23 > s sum(l,r) = 23 > s s u m ( l , r ) = 23 > s l l l
Tăng vị trí l l l 1 1 1
a = [ 2 , 6 , 5 , 3 , 6 , 8 l ↓ , 9 r ↓ ] a = [2, 6, 5, 3, 6, \overset{\underset{\downarrow}{\color{red}l}}{\color{green}8}, \overset{\underset{\downarrow}{\color{blue}r}}{\color{green}9}] a = [ 2 , 6 , 5 , 3 , 6 , 8 ↓ l , 9 ↓ r ] vì s u m ( l , r ) = 17 ≤ s sum(l,r) = 17 \leq s s u m ( l , r ) = 17 ≤ s [ l , r ] [l,r] [ l , r ]
a n s = m a x ( a n s , r − l + 1 ) ans = max(ans, r - l + 1) an s = ma x ( an s , r − l + 1 )
Cài đặt
Để có thể tính được tổng các phần tử từ l l l r r r l l l r r r s u m sum s u m [ l , r ] [l,r] [ l , r ]
Sau khi di chuyển r r r s u m sum s u m a [ r ] a[r] a [ r ]
Trước khi di chuyển l l l s u m sum s u m a [ l ] a[l] a [ l ]
int ans = 0, sum = 0;
for (int l = 1, r = 1; r <= n; r++) {
sum += a[r];
while (sum > s) {
sum -= a[l];
l++;
}
ans = max(ans, r - l + 1);
}
cout << ans;
Độ phức tạp
Vị trí con trỏ r r r l l l r r r
Hơn nữa, mỗi vị trí l l l r r r n n n
Vì thế độ phức tạp của giải pháp là O ( n ) O(n) O ( n )
Bạn được cho một dãy số nguyên như sau:
x 0 = 1 x_0=1 x 0 = 1 x i + 1 = ( a ⋅ x i + x i d i v b ) m o d c x_{i+1} = (a \cdot x_i + x_i \ div \ b) \ mod \ c x i + 1 = ( a ⋅ x i + x i d i v b ) m o d c
Tìm n n n m < n m < n m < n x m = x n x_m = x_n x m = x n n n n 2 ⋅ 1 0 7 2 \cdot 10^7 2 ⋅ 1 0 7
Giới hạn: 1 ≤ a ≤ 1 0 4 1 \leq a \leq 10^4 1 ≤ a ≤ 1 0 4 1 ≤ b , c ≤ 1 0 14 1 \leq b,c \leq 10^{14} 1 ≤ b , c ≤ 1 0 14
Để dễ dàng phân tích ta định nghĩa hàm f f f
f ( x ) = ( a ⋅ x + x d i v b ) m o d c f(x) = (a \cdot x + x \ div \ b) \ mod \ c
f ( x ) = ( a ⋅ x + x d i v b ) m o d c
Dãy số của chúng ta sẽ có dạng
x 0 = 1 , x 1 = f ( x 0 ) , x 2 = f ( x 1 ) , . . . , x i = f ( x i − 1 ) , . . . x_0 = 1, x_1=f(x_0), x_2=f(x_1),...,x_i=f(x_{i-1}),...
x 0 = 1 , x 1 = f ( x 0 ) , x 2 = f ( x 1 ) , ... , x i = f ( x i − 1 ) , ...
Với phép chia lấy dư cho c c c i > 0 i > 0 i > 0 x i x_i x i [ 0 , c − 1 ] [0, c-1] [ 0 , c − 1 ]
Vì thế, dãy số với vô hạn phần tử này sẽ tồn tại x m = x n x_m = x_n x m = x n m < n m < n m < n Dirichlet )
Có thể thấy, khi dãy tồn tại x m = x n x_m = x_n x m = x n
Gọi n n n m < n m < n m < n x m = x n x_m=x_n x m = x n
x 0 , x 1 , x 2 , . . . , x m ↑ , x m + 1 , . . . , x n − 1 , x n ↑ , . . . x_0,x_1, x_2,...,\underset{\uparrow}{x_m},x_{m+1},...,x_{n-1},\underset{\uparrow}{x_n},...
x 0 , x 1 , x 2 , ... , ↑ x m , x m + 1 , ... , x n − 1 , ↑ x n , ...
Khi đó, dãy sẽ có chu kỳ lặp lại các phần tử từ x m x_m x m x n − 1 x_{n-1} x n − 1
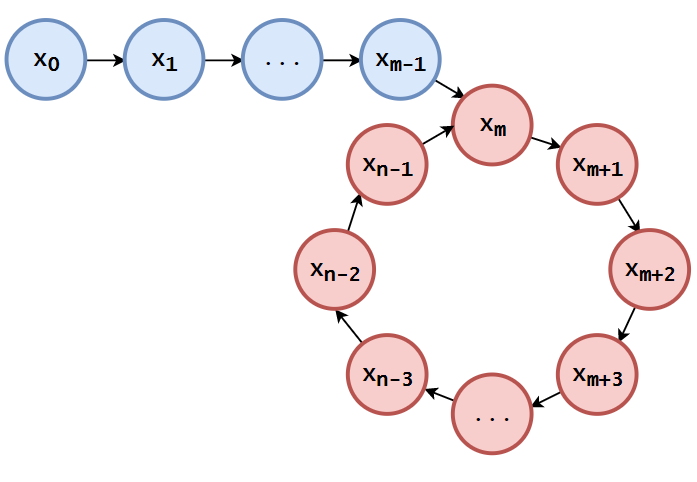
x 0 , x 1 , . . . , x m − 1 ⏟ , x m , x m + 1 , . . . , x n − 1 ⏟ , x m , x m + 1 , . . . , x n − 1 ⏟ , x m , x m + 1 , . . . , x n − 1 ⏟ , . . . {\color{blue}\underbrace{\color{black}x_0,x_1,...,x_{m-1}}_{}},{\color{red}\underbrace{\color{black}x_m,x_{m+1},...,x_{n-1}}_{}}, {\color{red}\underbrace{\color{black}x_m,x_{m+1},...,x_{n-1}}_{}}, {\color{red}\underbrace{\color{black}x_m,x_{m+1},...,x_{n-1}}_{}},...
x 0 , x 1 , ... , x m − 1 , x m , x m + 1 , ... , x n − 1 , x m , x m + 1 , ... , x n − 1 , x m , x m + 1 , ... , x n − 1 , ...
Dãy số có thể biễu diễn như hình sau đây:
Bài toán có thể giải quyết nếu chúng ta phần tử bắt đầu chu kỳ (x μ x_{\mu} x μ λ \lambda λ
Cụ thể, xem ví dụ sau đây:
a = 8 , b = 2 , c = 31 a = 8, b = 2, c = 31
a = 8 , b = 2 , c = 31
Ta có dãy số
1 , 8 , 6 , 20 , 15 ⏟ , 3 , 25 , 26 , 4 ⏟ , 3 , 25 , 26 , 4 ⏟ , 3 , 25 , 26 , 4 ⏟ , . . . {\color{blue}\underbrace{\color{black}1, 8, 6, 20, 15}_{}},{\color{red}\underbrace{\color{black}3, 25, 26, 4}_{}}, {\color{red}\underbrace{\color{black}3, 25, 26, 4}_{}}, {\color{red}\underbrace{\color{black}3, 25, 26, 4}_{}},...
1 , 8 , 6 , 20 , 15 , 3 , 25 , 26 , 4 , 3 , 25 , 26 , 4 , 3 , 25 , 26 , 4 , ...
Giá trị n n n n = 9 n = 9 n = 9
Ta có thể tính được giá trị này bằng cách xác định
phần tử bắt đầu chu kỳ x μ x_{\mu} x μ
độ dài chu kỳ λ \lambda λ
Ở đây, phần tử bắt đầu chu kỳ là x 5 x_5 x 5 4 4 4
Giá trị n = μ + λ = 5 + 4 = 9 n = \mu + \lambda = 5 + 4 = 9 n = μ + λ = 5 + 4 = 9
Để xác định giá trị μ \mu μ λ \lambda λ Floyd's tortoise and hare
Khởi tạo hai con trỏ, t o r o i s e toroise t oro i se h a r e hare ha re
Tại mỗi thời điểm, ta tịnh tiến hai con trỏ này như sau:
Tortoise (rùa): tịnh tiến một "bước"
Nếu hiện tại con trỏ t o r t o i s e tortoise t or t o i se x x x f ( x ) f(x) f ( x )
x 0 → x 1 → x 2 → x 3 → x 4 → . . . x_0 \rightarrow x_1 \rightarrow x_2 \rightarrow x_3 \rightarrow x_4 \rightarrow ... x 0 → x 1 → x 2 → x 3 → x 4 → ... Vì dãy số của chúng ta có chu kỳ nên ta có công thức tính giá trị của con trỏ t o r t o i s e tortoise t or t o i se t t t
t < μ t < \mu t < μ x t x_t x t t ≥ μ t \geq \mu t ≥ μ x μ + ( t − μ ) m o d λ x_{\mu+(t-\mu) \ mod \ \lambda} x μ + ( t − μ ) m o d λ
Hare (thỏ): tịnh tiến hai "bước"
Nếu hiện tại con trỏ h a r e hare ha re x x x f ( f ( x ) ) f(f(x)) f ( f ( x ))
x 0 → x 2 → x 4 → x 6 → x 8 → . . . x_0 \rightarrow x_2 \rightarrow x_4 \rightarrow x_6 \rightarrow x_8 \rightarrow ... x 0 → x 2 → x 4 → x 6 → x 8 → ... Vì dãy số của chúng ta có chu kỳ nên ta có công thức tính giá trị của con trỏ h a r e hare ha re t t t
2 t < μ 2t < \mu 2 t < μ x 2 t x_{2t} x 2 t 2 t ≥ μ 2t \geq \mu 2 t ≥ μ x μ + ( 2 t − μ ) m o d λ x_{\mu+(2t-\mu) \ mod \ \lambda} x μ + ( 2 t − μ ) m o d λ
Ngoài lúc ban đầu, hai con trỏ t o r t o i s e tortoise t or t o i se h a r e hare ha re
2 t < μ 2t < \mu 2 t < μ
Sau t t t t o r t o i s e tortoise t or t o i se x t x_t x t h a r e hare ha re x 2 t x_{2t} x 2 t
Tuy nhiên, μ + λ \mu + \lambda μ + λ x 0 x_0 x 0 x μ + λ − 1 x_{\mu + \lambda - 1} x μ + λ − 1
Vì thế x t ≠ x 2 t x_t \neq x_{2t} x t = x 2 t t o r t o i s e tortoise t or t o i se h a r e hare ha re
2 t ≥ μ 2t \geq \mu 2 t ≥ μ t < μ t < \mu t < μ
Sau t t t t o r t o i s e tortoise t or t o i se x t x_t x t h a r e hare ha re x μ + ( 2 t − μ ) m o d λ x_{\mu+(2t-\mu) \ mod \ \lambda} x μ + ( 2 t − μ ) m o d λ
Tuy nhiên, μ + λ \mu + \lambda μ + λ x 0 x_0 x 0 x μ + λ − 1 x_{\mu + \lambda - 1} x μ + λ − 1
Vì thế x t ≠ x μ + ( 2 t − μ ) m o d λ x_t \neq x_{\mu+(2t-\mu) \ mod \ \lambda} x t = x μ + ( 2 t − μ ) m o d λ t o r t o i s e tortoise t or t o i se h a r e hare ha re
t ≥ μ t \geq \mu t ≥ μ
Sau t t t t o r t o i s e tortoise t or t o i se x μ + ( t − μ ) m o d λ x_{\mu+(t-\mu) \ mod \ \lambda} x μ + ( t − μ ) m o d λ h a r e hare ha re x μ + ( 2 t − μ ) m o d λ x_{\mu+(2t-\mu) \ mod \ \lambda} x μ + ( 2 t − μ ) m o d λ
Giả sử t o r t o i s e tortoise t or t o i se h a r e hare ha re μ + ( t − μ ) m o d λ = μ + ( 2 t − μ ) m o d λ ⇔ t m o d λ = 0 \mu+(t-\mu) \ mod \ \lambda = {\mu+(2t-\mu) \ mod \ \lambda} \Leftrightarrow t \ mod \ \lambda = 0 μ + ( t − μ ) m o d λ = μ + ( 2 t − μ ) m o d λ ⇔ t m o d λ = 0
Vậy, t o r t o i s e tortoise t or t o i se h a r e hare ha re t t t t t t μ \mu μ λ \lambda λ
Trừ lúc khởi tạo, hai con trỏ t o r t o i s e tortoise t or t o i se h a r e hare ha re x μ + ( λ − μ m o d λ ) m o d λ x_{\mu+(\lambda -\mu \ mod \ \lambda) \ mod \ \lambda} x μ + ( λ − μ m o d λ ) m o d λ
Cách cài đặt để t o r t o i s e tortoise t or t o i se h a r e hare ha re
int tortoise = 1, hare = 1;
while (true) {
tortoise = f(tortoise);
hare = f(f(hare));
if (tortoise == hare)
break;
}
Khởi tạo một con trỏ mới p = x 0 p=x_0 p = x 0 t o r t o i s e tortoise t or t o i se
Tịnh tiến cùng lúc hai con trỏ p p p t o r t o i s e tortoise t or t o i se
Số lần tịnh tiến ở đây chính là μ \mu μ
Chứng minh:
Trong những lần tịnh tiến từ 0 0 0 μ − 1 \mu - 1 μ − 1 p p p x 0 x_0 x 0 x μ − 1 x_{\mu -1} x μ − 1 t o r t o i s e tortoise t or t o i se t o r t o i s e tortoise t or t o i se t o r t o i s e tortoise t or t o i se p p p
Hai con trỏ p p p t o r t o i s e tortoise t or t o i se μ \mu μ
Con trỏ p p p x μ x_{\mu} x μ
Lúc chưa tịnh tiến p p p t o r t o i s e tortoise t or t o i se x μ + ( t − μ ) m o d λ x_{\mu+(t-\mu) \ mod \ \lambda} x μ + ( t − μ ) m o d λ μ \mu μ t o r t o i s e tortoise t or t o i se x μ + ( t ) m o d λ x_{\mu+(t) \ mod \ \lambda} x μ + ( t ) m o d λ t t t λ \lambda λ t o r t o i s e tortoise t or t o i se x μ x_{\mu} x μ
Cách cài đặt tìm μ \mu μ
int mu = 0, p = 1;
while (p != tortoise) {
p = f(p);
tortoise = f(tortoise);
mu++;
}
Bây giờ cả hai con trỏ t o r t o i s e tortoise t or t o i se p p p x μ x_{\mu} x μ
Chúng ta giữ nguyên giá trị t o r t o i s e tortoise t or t o i se p p p p p p x μ x_{\mu} x μ
Vì p p p λ \lambda λ p p p x μ x_{\mu} x μ
int lambda = 0;
while (true) {
lambda++;
p = f(p);
if (tortoise == p)
break;
}
Để hiểu rõ hơn, ta hãy cùng xem qua một số ví dụ sau đây:
a = 2 , b = 2 , c = 32 a = 2, b = 2, c = 32
a = 2 , b = 2 , c = 32
Ta có dãy số
1 , 2 , 5 , 12 ⏟ , 30 , 11 , 27 , 3 , 7 , 17 , 10 , 25 ⏟ , 30 , 11 , 27 , 3 , 7 , 17 , 10 , 25 ⏟ , 30 , 11 , 27 , 3 , 7 , 17 , 10 , 25 ⏟ , . . . {\color{blue}\underbrace{\color{black}1, 2, 5, 12}_{}},{\color{red}\underbrace{\color{black}30, 11, 27, 3, 7, 17, 10, 25}_{}}, {\color{red}\underbrace{\color{black}30, 11, 27, 3, 7, 17, 10, 25}_{}}, {\color{red}\underbrace{\color{black}30, 11, 27, 3, 7, 17, 10, 25}_{}},...
1 , 2 , 5 , 12 , 30 , 11 , 27 , 3 , 7 , 17 , 10 , 25 , 30 , 11 , 27 , 3 , 7 , 17 , 10 , 25 , 30 , 11 , 27 , 3 , 7 , 17 , 10 , 25 , ...
Giá trị n n n n = 12 n = 12 n = 12
Ta có thể tính được giá trị này bằng cách xác định
phần tử bắt đầu chu kỳ x μ x_{\mu} x μ
độ dài chu kỳ λ \lambda λ
Ở đây, phần tử bắt đầu chu kỳ là x 4 x_4 x 4 8 8 8
Giá trị n = μ + λ = 4 + 8 = 12 n = \mu + \lambda = 4 + 8 = 12 n = μ + λ = 4 + 8 = 12
Độ phức tạp
Khi khởi tạo hai con trỏ t o r t o i s e tortoise t or t o i se h a r e hare ha re x 0 x_0 x 0 t t t
Cụ thể t t t t t t μ \mu μ λ \lambda λ
Vì thế việc xác định được vị trí t o r t o i s e tortoise t or t o i se h a r e hare ha re μ + λ \mu + \lambda μ + λ μ \mu μ μ \mu μ λ \lambda λ λ \lambda λ
Kết luận: độ phức tạp của bài toán là O ( μ + λ ) O(\mu + \lambda) O ( μ + λ ) μ + λ ≤ 2 ⋅ 1 0 7 \mu + \lambda \leq 2 \cdot 10^7 μ + λ ≤ 2 ⋅ 1 0 7
.gif)
.gif)
.gif)
.gif)
.gif)