¶ Chia Căn Phần I
Tác giả
- Lê Tuấn Hoàng - National University of Singapore
Reviewer
- Trần Xuân Bách - University of Chicago
- Nguyễn Minh Nhật - Georgia Tech
¶ Lời nói đầu
Chia căn, một kĩ thuật thú vị, thiên biến vạn hóa qua từng bài tập.
Những kĩ thuật, thuật toán vận dụng các tính chất của phép căn thường được gọi chung là chia căn. Bài viết được biên soạn nhằm mang đến cho bạn đọc cái nhìn chi tiết nhất về chia căn và những vấn đề liên quan.
Các kĩ thuật được trình bày sẽ đi kèm một vài bài toán ví dụ, được đưa vào giúp bạn đọc dễ hình dung về ứng dụng của kĩ thuật hơn. Chia căn có thể không phải lời giải tối ưu nhất cho bài toán ví dụ. Cài đặt mẫu được cài đặt bằng ngôn ngữ C++ và được cài đặt tường minh nhất nên có thể chưa được tối ưu.
¶ Kiến thức cần biết
¶ Xử lí online và offline
Bài viết sẽ nhắc tới hai khái niệm này tương đối nhiều, nên xin phép bạn đọc được giải thích hai khái niệm này.
Hai khái niệm thường được sử dụng trong các bài toán xử lí truy vấn. Cụ thể:
- Xử lí offline: Ta có thể đọc vào tất cả các truy vấn. Sau đó có thể xử lí tuần tự từng truy vấn một hoặc có thể xử lí các truy vấn theo một thứ tự hợp lí khác để giải quyết bài toán hiệu quả.
- Xử lí online:
- Ta không thể đọc được vào toàn bộ các truy vấn. Thông tin về các truy vấn sẽ được mã hóa, cần xử lí được truy vấn trước đó để giải mã.
- Ví dụ: Khi xử lí truy vấn cần số nguyên , đề bài sẽ cho số nguyên . Sau đó được tính bằng công thức với là kết quả của truy vấn trước đó. Các truy vấn hoàn toàn bị phụ thuộc vào các truy vấn trước, không có cách nào ngoài việc xử lí tuần tự các truy vấn.
¶ Quy hoạch động
Một số bài toán dưới đây sử dụng quy hoạch động. Bạn đọc nên nắm được quy hoạch động cơ bản.
Phần I của bài viết xin được trình bày về các kĩ thuật chia căn thường gặp hơn.
¶ 1. Chia căn dựa vào phân tích tổng số nguyên dương
Có nhận xét: Nếu số nguyên dương được tách thành tổng của các số nguyên dương, thì tồn tại không quá số nguyên dương khác nhau.
Chứng minh
Để cực đại số lượng số khác nhau, ta sẽ chọn những số nhỏ nhất có thể: Nếu chọn các số nguyên từ đến , tổng của chúng là . Vậy nên số lượng giá trị khác nhau không vượt quá .
Dưới đây là một số bài toán sử dụng tính chất này.
¶ Bài toán 1: Codeforces 221D - Little Elephant and Array
¶ Tóm tắt đề bài
Cho mảng gồm phần tử thỏa mãn . Có truy vấn , hãy đếm số lượng giá trị xuất hiện đúng lần nằm trong đoạn .
¶ Lời giải
Để một giá trị xuất hiện đúng lần trong đoạn thì phải xuất hiện ít nhất lần trong đoạn . Do đó, ta chỉ quan tâm những giá trị , còn các giá trị không thể xuất hiện ít nhất lần trong dãy nên không cần đếm chúng.
Số lượng giá trị ta cần quan tâm nhiều nhất khi: Có đúng giá trị xuất hiện lần, giá trị xuất hiện lần,.... Dễ thấy, số lượng giá trị cần quan tâm nhiều nhất là khoảng .
Từ đây, trong mỗi truy vấn, với từng giá trị cần xét, ta chỉ cần lần lượt kiểm tra số lần xuất hiện của nó trong đoạn có chính xác là hay không.
¶ Cài đặt
int n, q, a[N];
// Mảng đếm giá trị
int cnt[N];
// Lưu những giá trị cần phải xét
vector<int> value;
vector<vector<int>> prefix_sums;
// Phần khởi tạo
void init(){
for(int i = 1; i <= n; i++){
cin >> a[i];
if (a[i] <= n)
cnt[a[i]]++;
}
for(int x = 1; x <= n; x++){
// Điều kiện để giá trị x được xét là có số lần xuất hiện ít nhất x lần, có không quá 2 * sqrt(n) giá trị cần xét
if(cnt[x] >= x){
value.push_back(x);
// Mảng cộng dồn phục vụ việc đếm số lượng giá trị x nằm trong một đoạn liên tiếp với độ phức tạp thời gian O(1)
vector<int> prefix_sum(n + 1);
for(int i = 1; i <= n; i++){
prefix_sum[i] = prefix_sum[i - 1] + (a[i] == x);
}
prefix_sums.push_back(prefix_sum);
}
}
}
// Phần truy vấn
int query(int l, int r){
int answer = 0;
for(int i = 0, _ = value.size(); i < _; i++){
if(prefix_sums[i][r] - prefix_sums[i][l - 1] == value[i]){
answer++;
}
}
return answer;
}
Độ phức tạp của phần khởi tạo là , độ phức tạp của một truy vấn là . Độ phức tạp của thuật toán là .
¶ Bài toán 2: MarisaOJ - Ghép xâu
¶ Đề bài
Cho tập gồm xâu khác nhau có tổng độ dài là và một xâu mục tiêu . Hỏi có bao nhiêu cách để có thể ghép được xâu từ xâu đã cho. Một xâu có thể được sử dụng nhiều lần.
Ví dụ với xâu = ABAB và A, B, AB thì có cách ghép:
A+B+A+BA+B+ABAB+A+BAB+AB
¶ Giới hạn
- .
- .
- .
¶ Quy hoạch động
Có thể sử dụng quy hoạch động để giải bài toán này: Hàm mục tiêu là , là số lượng cách để ghép được tiền tố .
Để giải bài toán hiệu quả, ta cần sử dụng thuật toán hash nhằm so sánh tính bằng nhau của các xâu trong độ phức tạp thời gian .
Để tính được , ta xét toàn bộ các xâu con của kết thúc tại , kiểm tra xem nó có thuộc tập đã cho hay không và cập nhật tương ứng.
// Tập H lưu mã hash của các xâu trong tập S
unoredered_set<int64_t> H;
...
// Sử dụng index từ 1 sẽ thuận tiện hơn trong bài toán này
T = "#" + T;
for(int i = 1; i < T.size(); i++){
for(int j = i; j >= 1; j--){
// Tính hash của xâu con T[j...i]
int64_t hash_value = get_hash(j, i);
// Nếu trong tâp S có tồn tại xâu bằng với xâu con này
if(H.count(hash_value)){
count[i] += count[j - 1];
}
}
}
Thuật toán này có độ phức tạp .
¶ Chia căn
Ta có nhận xét là có tối đa độ dài xâu khác nhau trong tập . Để tính , thay vì xét toàn bộ các xâu con kết thúc tại , ta chỉ cần xét các xâu con có độ dài kết thúc ở , sao cho tồn tại ít nhất một xâu có độ dài trong tập . Phần cài đặt khá tương tự:
// Tập H[i] lưu mã hash của các xâu độ dài i trong tập S
unordered_set<int64_t> H[N];
// Danh sách các độ dài xâu khác nhau của các xâu trong tập S
vector<int> lengths;
...
T = "#" + T;
for(int i = 1; i < T.size(); i++){
for(int &p : lengths){
int64_t hash_value = get_hash(i - p + 1, i);
if(H[p].count(hash_value)){
count[i] += count[i - p];
}
}
}
Do không có quá độ dài khác nhau nên độ phức tạp chỉ là .
¶ Mở rộng: Thuật toán tất định
Ngoài cách sử dụng hash, ta cũng có thể sử dụng thuật toán Aho-Corasick.
Tương tự, có độ dài xâu khác nhau. Với mỗi độ dài , dựng máy trạng thái hữu hạn (finite state machine - FSM) gồm các xâu có độ dài trong tập .
Để tính được , sử dụng kí tự để di chuyển đến trạng thái tiếp theo trên toàn bộ các FSM đã xây dựng. Nếu trạng thái của FSM gồm các xâu độ dài là kết thúc của một xâu, có thể khẳng định xâu con tồn tại trong và tiến hành cập nhật tương ứng.
¶ Bài toán 3: MarisaOJ - Cái túi
¶ Đề bài
Cho vật có khối lượng lần lượt là và . Hãy kiểm tra xem có thể chọn một số vật sao cho tổng khối lượng của chúng là không?
¶ Giới hạn
- .
¶ Quy hoạch động
Dễ thấy đây là bài quy hoạch động cái túi điển hình có thể giải được trong độ phức tạp thời gian là .
Để làm tốt hơn, ta có nhận xét đầu tiên là có không quá khối lượng các nhau, phân các vật có cùng khối lượng vào cùng một nhóm.
Vẫn sử dụng quy hoạch động cái túi: Hàm mục tiêu của ta sẽ là là hoặc tương ứng với sau khi xét xong nhóm khối lượng đầu tiên, có thể tạo ra được khối lượng không? Ta có thể cài đặt như sau:
// d là số lượng khối lượng khác nhau
// W[i] là khối lương của nhóm thứ i
// c[i] là số lượng của nhóm thứ i
for(int i = 1; i <= d; i++){
for(int p = 0; p <= T; p++){
// k là số lượng vật lấy ở trong nhóm thứ i
for(int k = 0; k * W[i] <= p, k <= c[i]; k++){
if(possible[i - 1][p - k * W[i]])
possible[i][p] = true;
}
}
}
Nếu cài đặt như này, độ phức tạp vẫn là . Cách chuyển nhãn là: khi tồn tại sao cho . Ta có một nhận xét quan trọng , điểm đặc biệt này dẫn tới cách làm như sau:
// last[u] lưu lại vị trí gần nhất mà possible[i - 1][p'] = true sao cho p' mod W[i] = u
for(int i = 1; i <= d; i++){
memset(last, -1, sizeof last);
for(int p = 0; p <= T; p++){
// Cần phải sử dụng <= c[i] vật
if(last[p % W[i]] != -1 && (p - last[p % W[i]]) / W[i] <= c[i]){
possible[i][p] = true;
}
if(possible[i - 1][p]){
last[p % W[i]] = p;
}
}
}
Ta thu được thuật toán có độ phức tạp .
¶ 2. Thuật toán Mo
¶ Bài toán 1: VNOJ - Hamilton Path
Bài toán này tuy không sử dụng thuật toán Mo, nhưng sẽ là tiền đề khi tìm hiểu về thuật toán Mo.
¶ Đề bài
Cho điểm trên hệ trục tọa độ . Khoảng cách giữa hai điểm là (khoảng cách Manhattan).
Đường đi Hamilton là đường đi đi qua toàn bộ điểm và mỗi điểm chính xác một lần. Với là một hoán vị của các số nguyên từ tới , độ dài đường đi Hamilton được tính bằng công thức .
Hãy tìm một đường đi Hamilton có độ dài không quá . Không bắt buộc cực tiểu hóa độ dài đường đi.
¶ Lời giải
Ta sẽ chia hình vuông ban đầu thành hình chữ nhật . Ta sẽ lần lượt đi qua từng hình chữ nhật một, và đi qua các điểm trong cùng một hình chữ nhật theo tung độ không giảm nếu chỉ số của hình chữ nhật là lẻ và giảm dần nếu chỉ số là chẵn.
Ví dụ như hình dưới đây. Để dễ hình dung, hình mẫu sử dụng hình vuông và chia thành hình chữ nhật . Các đường nối thể hiện thứ tự của các điểm, không phải khoảng cách Manhattan.
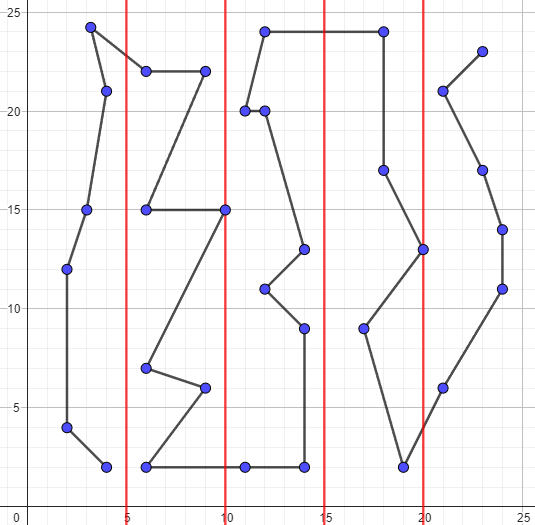
Để tính được độ dài đường đi, ta thấy số bước đi theo trục tung và số bước đi theo trục hoành là độc lập:
- Do tung độ sắp xếp không giảm, nên tổng số bước của các điểm theo trục tung trong một hình chữ nhật tối đa là . Có hình chữ nhật, nên tổng số bước đi theo trục tung không vượt quá .
- Khi di chuyển giữa các điểm ở trong cùng một hình chữ nhật sẽ không đi quá bước theo trục hoành, khi di chuyển từ một điểm ở hình chữ nhật này sang một điểm ở hình chữ nhật khác sẽ đi không quá bước. Có điểm cũng như không chuyển hình chữ nhật quá lần, nên số bước đi theo trục hoành là .
- Vây cận trên của độ dài đường đi Hamilton nếu đi theo cách này là , thỏa mãn yêu cầu đề bài.
¶ Bài toán 2: Codeforces 86D - Powerful array
¶ Tóm tắt đề bài
Cho mảng gồm phần tử nguyên dương có giá trị. Cho truy vấn . Xét đoạn con , với là số lần xuất hiện của giá trị trong đoạn, sức mạnh của đoạn con này là tổng của tất cả các tích . Với mỗi truy vấn, hãy tính sức mạnh của mảng con đã cho.
¶ Giới hạn
- .
- .
¶ Thuật toán ngây thơ
Với mỗi truy vấn, ta dùng vòng lặp để lặp qua từng phần tử nhằm mục đích đếm số lần xuất hiện của từng giá trị sử dụng mảng đếm. Cuối cùng tính sức mạnh dựa vào mảng đếm hoặc các cấu trúc dữ liệu như std::unordered_map. Thuật toán này là không đủ tốt với độ phức tạp .
¶ Thuật toán cải tiến
Trước tiên ta sẽ cải tiến thuật toán một chút, thay vì tính lại toàn bộ thông tin với từng truy vấn, ta lợi dụng thông tin đã tính ở truy vấn trước đó để giảm số phần tử phải xét.
Ví dụ, nếu trước đó ta xử lí truy vấn và truy vấn kế tiếp là , ta nhận thấy hai đoạn con này có chung đoạn , ta chỉ phải thêm phần tử và xóa phần tử trong mảng đếm, cùng lúc đó tính lại đáp án. Phương pháp này so với khởi tạo lại mảng đếm và đếm lại từ đầu thì có tốt hơn.
// Tham số value là giá trị cần thêm hoặc xóa
// Tham số delta là 1 tương ứng với thêm, -1 là xóa
int current_answer;
void update(long long value, int delta){
// Khi thay đổi giá trị trong mảng đếm đồng thời cập nhật lại đáp án hiện tại
current_answer -= count[value] * count[value] * value;
count[value] += delta;
current_answer += count[value] * count[value] * value;
}
Một cách tổng quát, nếu truy vấn trước đó là , truy vấn sau là :
- Nếu , ta cần xóa đoạn .
- Nếu , ta cần thêm đoạn .
Tương tự:
- Nếu , ta cần thêm đoạn .
- Nếu , ta cần xóa đoạn .
Vậy số lượng phần tử cần thêm/xóa là giữa hai truy vấn là . Và số lần cần thêm/xóa qua toàn bộ các truy vấn là: .
Nhưng độ phức tạp trong trường hợp tệ nhất của thuật toán trên vẫn là . Ví dụ với bộ test với và các truy vấn cố tình được sinh như sau:
Có thể thấy khoảng cách giữa hai đầu mút giữa hai truy vấn liên tiếp là rất lớn.
¶ Thuật toán Mo
Bài toán có thể xử lí offline. Mấu chốt của thuật toán Mo là việc sắp xếp lại các truy vấn theo thứ tự hợp lí để đảm bảo tổng chi phí di chuyển giữa các truy vấn là đủ tốt.
Với mỗi truy vấn , ta có thể coi nó như một điểm trên hệ tọa độ. Chi phí để chuyển từ truy vấn sang truy vấn là , chính là khoảng cách Manhattan giữa hai điểm và .
Có điểm tương ứng với truy vấn, sắp xếp lại thứ tự các điểm sao cho tổng khoảng cách Manhattan giữa hai điểm liên tiếp là nhỏ nhất, và đó cũng chính là bài toán Hamilton Path được trình bày ở trên!
Ta sẽ sắp xếp các truy vấn giống như cách sắp xếp các điểm trong bài toán Hamilton Path:
- Đầu tiên chia các chỉ số vào các nhóm, cứ chỉ số thì vào một nhóm (giá trị sẽ được trình bày ở dưới), cụ thể chỉ số sẽ vào nhóm . Thao tác này tương ứng với thao tác chia hình chữ nhật.
- Tiếp theo sắp xếp các truy vấn theo chỉ số nhóm của đầu mút trái, tạm gọi giá trị này là . Thao tác này tương ứng với việc đi qua lần lượt từng hình chữ nhật.
- Cuối cùng, các truy vấn có cùng sẽ được sắp xếp theo đầu mút phải không giảm lẻ, không tăng nếu chẵn. Thao tác này tương ứng với các điểm trong cùng hình chữ nhật được sắp xếp không giảm hoặc không tăng theo tung độ tùy vào tính chẵn lẻ của hình chữ nhật.
Dưới đây là hàm so sánh khi sắp xếp các truy vấn viết bằng C++:
struct query{
int l, r; // hai đầu mút của truy vấn
int id; // chỉ số của truy vấn, vì sau khi sắp xếp ta sẽ mất thứ tự ban đầu
}
bool cmp(const query &a, const query &b){
if(a.l / S != b.l / S) // nếu đầu mút trái của hai truy vấn thuộc hai nhóm khác nhau
return a.l < b.l; // sắp xếp dựa trên đầu mút trái
// ngược lại nếu chỉ số nhóm của đầu mút trái lẻ thì sắp xếp không tăng theo đầu mút phải
if((a.l / S) % 2 == 1)
return a.r < b.r;
else
return a.r > b.r
}
Để chọn được tối ưu: Chia mỗi nhóm giá trị, vậy là có nhóm.
Số lần di chuyển đầu mút trái (từ đến ):
- Nếu và thuộc cùng một nhóm: Số bước di chuyển là không quá . Vậy số thao tác không vượt quá .
- Nếu và khác nhóm: Tổng số bước không vượt quá .
Số lần di chuyển đầu mút phải (từ đến ):
- Nếu và thuộc cùng một nhóm: Do đầu mút phải được sắp xếp tăng dần nên số thao tác di chuyển đầu mút phải không vượt quá . Có nhóm, nên số thao tác không vượt quá .
- Nếu và khác nhóm: Do điều chỉnh cách sắp xếp mỗi khi đổi nhóm, tổng số thao tác trong cả hai trường hợp vẫn không vượt quá .
Ta cần chọn sao cho nhỏ nhất. Theo bất đẳng thức AM-GM, đạt được giá trị nhỏ nhất khi , độ phức tạp thuật toán là .
¶ Cài đặt mẫu
Phần cài đặt còn lại có thể như sau:
long long current_answer = 0;
void update(long long value, int delta){
current_answer -= cnt[value] * cnt[value] * value * delta;
cnt[val] += delta;
current_answer += cnt[value] * cnt[value] * value * delta;
}
int main(){
//...
sort(q + 1, q + Q + 1, cmp);
// l, r là đầu mút của đoạn đang xét hiện tại
int l = 1, r = 0;
for(int i = 1; i <= Q; i++){
// Cần di chuyển hai đầu mút l, r đến truy vấn mới
while(l < q[i].l) update(a[l++], -1);
while(l > q[i].l) update(a[--l], 1);
while(r < q[i].r) update(a[++r], 1);
while(r > q[i].r) update(a[r--], -1);
ans[q[i].id] = current_answer;
}
//...
}
¶ Bài tập
- VNOJ - D-Query
- Codeforces 877E - Ann and books
- MarisaOJ - Tần suất
- Codeforces 617E - XOR and Favorite Number
¶ 3. Chia block
Đây là một kĩ thuật cũng thường được sử dụng để xử lí truy vấn trên mảng. Khác với thuật toán Mo, phương pháp chia block xử lí truy vấn cập nhật và trả lời truy vấn online dễ dàng hơn.
Để code được ngắn gọn, ở trong kĩ thuật này, chỉ số mảng trong các cài đặt bắt đầu từ . Các bài toán có chỉ số mảng bắt đầu từ cần chuyển đổi phù hợp.
¶ Bài toán 1: VNOJ - Point update, range query
¶ Tóm tắt đề bài
Cho mảng gồm phần tử nguyên. Cho truy vấn thuộc một trong hai dạng:
1 i x: Gán .2 l r: Tính tổng các phần tử .
¶ Giới hạn
- .
- .
- .
¶ Chia block
Chọn một hằng số , ta chia mảng thành các block phần tử liên tiếp, như vậy sẽ có nhóm. Nói cách khác, phần tử thứ thuộc nhóm . Phần tử đầu tiên của nhóm thứ là , phần tử cuối cùng là :
Ví dụ với dãy có phần tử, ta chọn và chia thành dãy thành block.
| 21 | 17 | 20 | 13 | ||||||||||||
| 5 | 8 | 6 | 3 | 2 | 7 | 2 | 6 | 7 | 1 | 7 | 5 | 6 | 2 | 3 | 2 |
Xử lí truy vấn cập nhật : Ta chỉ cần thay đổi cũng như tổng của các phần tử trong block chứa . Độ phức tạp của thao tác này là . Ví dụ phần tử mang giá trị được cập nhật thành , thì tổng của block đó cũng được cập nhật thành .
| 21 | 15 | 20 | 13 | ||||||||||||
| 5 | 8 | 6 | 3 | 2 | 5 | 2 | 6 | 7 | 1 | 7 | 5 | 6 | 2 | 3 | 2 |
Xử lí truy vấn tính tổng : Ta tính tổng những block nằm gọn trong đoạn truy vấn và một số phần tử lẻ ra ở hai bên. Như ví dụ, tổng của đoạn truy vấn là
| 21 | 15 | 20 | 13 | ||||||||||||
| 5 | 8 | 6 | 3 | 2 | 5 | 2 | 6 | 7 | 1 | 7 | 5 | 6 | 2 | 3 | 2 |
Có không quá block, và số lượng phần tử thừa ra hai bên không vượt quá nên truy vấn tính tổng cùa độ phức tạp .
Cụ thể hơn, với truy tính tổng, ta sẽ có hai bước, với là block chứa và là block chứa :
- Tính tổng các block từ đến .
- Tính tổng các phần tử trong hai phần thừa và .
- Chú ý trường hợp đặc biệt .
Độ phức tạp của bài toán là .
¶ Cài đặt
Truy vấn cập nhật:
// sum[b] là tổng của block thứ b
void update(int i, int x){
sum[i / S] -= a[i];
a[i] = x;
sum[i / S] += a[i];
}
Truy vấn tính tổng:
int sum(int l, int r){
int answer = 0;
// Block chứa l và r
int block_l = l / S;
int block_r = r / S;
// Trường hợp l và r nằm cùng block phải xử lí riêng
if(block_l == block_r){
for(int i = l; i <= r; i++){
answer += a[i];
}
}else{
// Tính tổng những phần thừa hai bên
for(int i = l; i < (block_l + 1) * S; i++){
answer += a[i];
}
for(int i = block_r * S; i <= r; i++){
answer += a[i];
}
// Tính tổng những block nằm hoàn toàn trong truy vấn
for(int i = block_l + 1; i < block_r; i++){
answer += sum[i];
}
}
return answer;
}
¶ Bài toán 2
¶ Đề bài
Cho mảng gồm phần tử nguyên dương. Cho truy vấn thuộc một trong hai dạng:
1 l r k: Đếm số lượng giá trị bằng trong đoạn con .2 l r x: Tăng các phần tử trong đoạn con lên .
¶ Giới hạn
- .
- .
- .
¶ Nếu các truy vấn đều có và
Đầu tiên ta sẽ cần sử dụng một cấu trúc dữ liệu để thống kê số lần xuất hiện của từng giá trị ở trong mảng , do các giá trị lớn nên ta chọn sử dụng std::map.
Với truy vấn cập nhật giá trị các phần tử, ta sẽ không trực tiếp thay đổi giá trị của phần tử mà lưu một biến , thể hiện các phần tử trong mảng đã được tăng lên bao nhiêu. Mỗi một lần cập nhật lại tăng lên . Truy vấn cập nhật có độ phức tạp .
Với truy vấn đếm số lượng giá trị bằng , ta biết các phần tử trong mảng đã được tăng lên , nên cần đếm trong cấu trúc dữ liệu đã được chuẩn bị ban đầu có bao nhiêu giá trị bằng . Truy vấn đếm có độ phức tạp .
¶ Bài toán gốc
Chia mảng thành các block phần tử. Áp dụng tương tự cách làm cho trường hợp , với mỗi block ta khởi tạo một cấu trúc dữ liệu đếm giá trị trong block đó.
Với những truy vấn cập nhật, đầu tiên ta cập nhật lại những block nằm hoàn toàn trong đoạn cần cập nhật. Ta lưu với ý nghĩa block đã được tăng lên bao nhiêu:
void update_block(int block_l, int block_r, int x){
for(int i = l; i <= r; i++){
lazy[i] += x;
}
}
Tiếp theo là đến bước cập nhật các phần thừa ở hai bên, do số phần tử ít nên có thể duyệt qua từng phần tử và cập nhật. Nhưng cần lưu ý là áp dụng cho trọn vẹn block . Cập nhật phần thừa chỉ cập nhật lại một phần của block, vì vậy nên trước khi cập nhật phần thừa, phải cập nhật thực sự vào các phần tử.
// count[i][j] là số lượng giá trị j nằm trong block i
map<int, int> count[];
void apply_lazy(int b){
count[b].clear();
// Cập nhật lazy[b] vào từng phần tử trong block b
for(int i = b * S; i < (b + 1) * S; i++){
a[i] += lazy[b];
count[b][a[i]]++;
}
lazy[b] = 0;
}
// Cập nhật thủ công từ phần tử l đến r
void manual_update(int l, int r, int x){
int b = l / S;
for(int i = l; i <= r; i++){
count[b][a[i]]--;
if(count[b][a[i]] == 0){
count[b].erase(a[i]);
}
a[i] += x;
count[b][a[i]]++;
}
}
void update(int l, int r, int x){
int block_l = l / S;
int block_r = r / S;
// Không quên trường hợp đặc biệt l, r nằm cùng trong một block
if(block_l == block_r){
apply_lazy(block_l);
manual_update(l, r, x);
}else{
update_block(block_l, block_r, x);
// Phải cập nhật lazy vào các block chứa l, r trước khi cập nhật phần thừa
apply_lazy(block_l);
apply_lazy(block_r);
// Phần thừa
manual_update(l, (block_l + 1) * S - 1, x);
manual_update(block_r * S, r, x);
}
}
Và khi truy vấn, ta đếm số lượng giá trị bằng trong từng block nguyên vẹn, và duyệt qua từng phần tử ở phần thừa.
Cả hai loại truy vấn có độ phức tạp , nên độ phức tạp cuối cùng là .
¶ Bài toán 3: MarisaOJ - Yếu vị
¶ Tóm tắt đề bài
Cho một mảng gồm phần tử nguyên dương. Cho truy vấn có dạng , hãy tìm số lần xuất hiện của phần tử xuất hiện nhiều nhất (số yếu vị) trong đoạn . Các truy vấn phải xử lí online.
¶ Giới hạn
- .
¶ Chia block
Ở bài toán này, ta cũng chia mảng đã cho thành block liên tiếp, mỗi block gồm phần tử.
Ở bài toán 1, 2, ta tính đáp án cho từng block, phần thừa rồi kết hợp chúng lại để ra đáp án cuối cùng.
Trong bài toán này, ta cũng có thể dễ dàng tìm được giá trị xuất hiện nhiều nhất trong một block cùng số lần xuất hiện của nó. Nhưng liệu có tồn tại cách để kết hợp đáp án các block lại một cách hiệu quả?
Vì vậy, ta sẽ có cách tiếp cận khác.
Định nghĩa giá trị xuất hiện nhiều nhất trong các block . Ta sẽ tính trước toàn bộ với .
Nếu truy vấn bao toàn bộ các block . Có thể khẳng định trị xuất hiện nhiều nhất trong đoạn sẽ là hoặc một giá trị nằm trong phần thừa ở hai bên.
Chứng minh: Giả sử giá trị xuất hiện nhiều nhất là không phải cũng như không nằm trong phần thừa, thì chắc chắn chỉ xuất hiện trong các block . Nhưng điều này đồng nghĩa với việc chính là . Vậy có thể kết luận điều này không xảy ra!
Như vậy có nhiều nhất ứng viên cho số yếu vị của đoạn , nhiệm vụ còn lại là kiểm tra lần lượt từng giá trị này, đếm số lần xuất hiện trong đoạn truy vấn, và chọn ra giá trị xuất hiện nhiều nhất. Đếm số lần xuất hiện của một giá trị trên một đoạn con liên tiếp là bài toán cơ bản sử dụng tìm kiếm nhị phân.
Với thuật toán này, phần tính trước có độ phức tạp và phần truy vấn có độ phức tạp .
Bài toán cũng tồn tại lời giải với độ phức tạp tốt hơn là , cần cải tiến một chút từ thuật toán trên.
¶ Nhận xét
Nhìn chung các bài toán sử dụng kĩ thuật chia block đều quy về việc xử lí được các block nguyên và phần thừa hai bên. Kĩ thuật có phần linh hoạt hơn thuật toán Mo do có thể hỗ trợ tốt hơn các thao tác cập nhật, cũng như trả lời được các truy vấn online.
¶ Bài tập
- VNOJ - Inversion counting
- VNOJ - Minimum distance
- VNOJ - Vua Kẹo
- Codeforces 13E - Holes
- Codechef - FNCS
¶ Danh sách bài tập
- VNOJ - Educational SQRT Contest 1
- VNOJ - Educational SQRT Contest 2
- VNOI: Các bài toán chia căn trên Codeforces được phân loại theo cách làm.
- MarisaOJ - Chia căn
- USACO - Square Root Decomposition