¶ Chia căn II
Tác giả
- Lê Tuấn Hoàng - National University of Singapore
Reviewer
- Trần Xuân Bách - University of Chicago
- Nguyễn Minh Nhật - Georgia Tech
Phần II của bài viết xin được trình bày về các kĩ thuật chia căn nâng cao hơn.
¶ Các kĩ thuật chia căn
¶ 1. Chia "nặng" và "nhẹ"
Kĩ thuật chia các "đối tượng", ở đây có thể là các truy vấn, đỉnh, xâu,..., thành hai nhóm "nặng" và "nhẹ" để có cách xử lí phù hợp.
Một nhận xét quan trọng thường được sử dụng trong kĩ thuật này: Nếu ta phân tích số nguyên dương thành tổng của các số nguyên dương khác (không nhất thiết phải đôi một phân biêt), có không quá số có giá trị lớn hơn hoặc bằng .
¶ Bài toán 1: MarisaOJ - Truy vấn cây
¶ Tóm tắt đề bài
Cho cây gồm đỉnh, trên mỗi đỉnh là giá trị . Cho truy vấn thuộc một trong hai dạng:
1 u d: Tăng các giá trị trên các đỉnh kề với thêm .2 u: Tìm giá trị trên đỉnh .
¶ Giới hạn
- .
- .
- .
¶ Thuật toán ngây thơ
Thuật toán đơn giản nhất chính là với mỗi truy vấn cập nhật, duyệt qua toàn bộ đỉnh kề của và tăng giá trị trên các đỉnh này. Trong trường hợp tệ nhất, thuật toán có độ phức tạp .
Vậy trường hợp tốt hơn thì sao? Đó là khi số lượng đỉnh kề, hay còn gọi là bậc, của không quá nhiều.
¶ Chia "nặng" và "nhẹ"
Đầu tiên ta có nhận xét: Tổng bậc của đỉnh là .
Từ đây phân loại các đỉnh vào hai nhóm:
- Nặng gồm các đỉnh có bậc lớn hơn . Sẽ có không quá đỉnh nặng.
- Nhẹ gồm các đỉnh còn lại, bậc nhỏ hơn hoặc bằng .
Để xử lí các truy vấn cập nhật của đỉnh nhẹ, ta hoàn toàn có thể sử dụng thuật toán ngây thơ ở trên do số lượng đỉnh kề nhỏ. Thao tác xử lí những truy vấn đỉnh nhẹ có độ phức tạp .
Để xử lí các truy vấn cập nhật của đỉnh nặng, ta sẽ sử dụng mảng và tăng lên để đánh dấu đỉnh này đã được cập nhật thêm . Thao tác xử lí cập nhật đỉnh nặng có độ phức tạp .
Với các truy vấn trả lời giá trị trên đỉnh , ngoài các giá trị đã được cập nhật trực tiếp qua các truy vấn đỉnh nhẹ, cần tính tổng với là các đỉnh kề của . Dĩ nhiên khi tính tổng , chỉ cần quan tâm đến các đỉnh nặng, mà có không quá đỉnh nặng nên các truy vấn trả lời có thể xử lí trong độ phức tạp .
¶ Bài toán 2: Codeforces 1207F - Remainder Problem
¶ Tóm tắt đề bài
Cho mảng gồm số nguyên được đánh số từ đến . Ban đầu tất cả các phần tử đều là .
Cho truy vấn thuộc một trong hai dạng:
1 x y: Tăng lên .2 x y: Tính tổng các phần tử trong mảng mà có chỉ số chia dư .
¶ Thuật toán ngây thơ
Với loại truy vấn đầu tiên, chỉ đơn giản tăng phần tử có chỉ số lên .
Trong truy vấn thứ hai, ta sẽ xét toàn bộ các chỉ số thỏa mãn (khoảng chỉ số) để tính tổng. Có thể thấy khi đủ lớn thì truy vấn sẽ chạy tương đối nhanh.
¶ Chia "nặng" và "nhẹ"
Đặt .
Từ đây phân loại các truy vấn tính tổng vào hai nhóm:
- Nặng gồm các truy vấn có lớn hơn . Các truy vấn này dễ dàng có thể được xử lí bằng thuật toán ngây thơ ở trên. Độ phức tạp thời gian là .
- Nhẹ gồm các truy vấn còn lại, có nhỏ hơn hoặc bằng .
Để xử lí các truy vấn nhẹ, ta sẽ lưu với là tổng của những chỉ số chia dư .
Khi thực hiện truy vấn cập nhật cho , với từng , ta cập nhật lại . Còn khi truy vấn, nếu thì in ra .
Thuật toán có độ phức tạp .
¶ Nhận xét
Khi chia các đối tượng ra thành "nặng" và "nhẹ", ta sẽ cần hai cách xử lí khác nhau. Thông thường một trong số chúng sẽ là thuật toán ngây thơ. Từ đây ta có hướng suy nghĩ để tìm ra lời giải trong dạng bài tập này: Tìm ra thuật toán vô cùng ngây thơ, trong trường hợp nào thì nó hiệu quả, và trong trường hợp không hiệu quả thì ta cần có cách giải quyết khác là gì?
¶ Bài tập
- VNOJ - DeMen100ns và thành phố
- MarisaOJ - Đỉnh gần nhất
- Codechef - KOL15C
- MarisaOJ - Màu thống trị
- MarisaOJ - Đếm xâu 3
- VNOJ - Demen và những truy vấn lẻ
- VNOJ - Subset sums
¶ 2. Chia căn truy vấn
Các thao tác cập nhật xuất hiện rất nhiều trong các bài toán xử lí truy vấn. Đôi khi, việc xử lí thao tác cập nhật khá khó, hoặc thậm chí không tồn tại cách cập nhật trực tiếp một cách hiệu quả. Đây chính là lúc kĩ thuật chia căn truy vấn tỏa sáng!
Kĩ thuật sẽ chia các truy vấn thành một số nhóm nhỏ, và sẽ chỉ thực hiện cập nhật cấu trúc (mảng, cây,...) sau khi xét xong một nhóm truy vấn.
¶ Bài toán 1
¶ Đề bài
Cho một bảng hình chữ nhật gồm ô. Ban đầu các ô trong bảng đều có màu trắng ngoại trừ một ô. Thực hiện truy vấn, mỗi truy vấn bạn cần tính khoảng cách từ một ô trắng được chỉ định tới ô đen gần nhất, rồi tô đen ô trắng đó.
Ví dụ với bảng sau:

Khoảng cách từ ô trắng mang dấu * đến ô đen gần nhất là , vì có thể đi sang bên trái hai bước để đến một ô đen. Sau đó tô đen ô này:

¶ Chia căn truy vấn
Ta có truy vấn, và sẽ chia chúng thành các nhóm truy vấn liên tiếp:
Khi xử lí hết một nhóm truy vấn, ta mới thực hiện tô đen những ô thuộc nhóm truy vấn này. Từ đây ta có hai trường hợp.
- Với những ô đen đã được tô trên bảng: Thực hiện thuật toán BFS đa nguồn để tính với mỗi ô trắng khoảng cách gần nhất tới một ô đen. Thao tác này có độ phức tạp .
- Với những ô đen chưa được tô nhưng nằm trước truy vấn đang xét: Chỉ cần xét toàn bộ những ô đen này và chọn ra ô có khoảng cách nhỏ nhất. Do có không quá ô đen cần xét nên độ phức tạp của thao tác này là .
Ta thực hiện thao tác thứ nhất lần, và với mỗi truy vấn thực hiện thao tác thứ hai, lời giải này có độ phức tạp .
¶ Bài toán 2: Timus - GCD 2010
¶ Tóm tắt đề bài
Bạn được cho một tập hợp rỗng gồm các số nguyên dương và truy vấn. Mỗi truy vấn sẽ thuộc một trong hai dạng, thêm một số vào tập hợp hoặc xóa một số khỏi tập hợp. Sau mỗi truy vấn hãy tính ước chung lớn nhất (GCD) của tất cả các số trong tập hợp. Lưu ý tập hợp có thể gồm nhiều số có giá trị giống nhau.
¶ Giới hạn
- .
- Các số trong tập hợp không vượt quá (đề bài gốc là , nhưng với thuật toán trình bày ở dưới có thể xử lí được tới giới hạn này).
¶ Chia căn truy vấn
Nếu biết được GCD hiện tại của các số trong tập hợp, việc thêm một số vào và tính lại GCD rất đơn giản. Nhưng khá khó để xóa một số khỏi tập hợp và tính lại GCD trong độ phức tạp thời gian đủ tốt.
Cách giải quyết sẽ là chia truy vấn thành các nhóm truy vấn.
Goi tập hợp đề bài cho là . Xử lí lần lượt các nhóm truy vấn. Khi xử lí đến nhóm thứ , ta tính xây dựng một tập hợp gồm các giá trị:
- Tồn tại trong tập hợp sau khi xử lí hết các nhóm truy vấn từ đến .
- Không tồn tại truy vấn xóa giá trị này trong nhóm .
Xét lần lượt các truy vấn trong nhóm : Nếu thực hiện hết các truy vấn từ đầu đến truy vấn này, có thể trong tập hợp sẽ bị thiếu một vài giá trị so với tập , nhưng sẽ không hề thừa giá trị nào, tránh được thao tác xóa khó thực hiện. Vì vậy chỉ cần tìm ra những giá trị bị thiếu rồi tính GCD của chúng với những giá trị trong tập .
Số giá trị bị thiếu tối đa trong mỗi truy vấn là và cứ truy vấn ta lại xây tập hợp gồm tối đa phần tử, vậy độ phức tạp của bài toán là .
¶ Nhận xét:
Bằng cách chia căn truy vấn, các bài toán đều được giải với các cách làm đơn giản và gần gũi hơn. Việc cập nhật lại cả cấu trúc tuy có độ phức tạp lớn nhưng không cần thực hiện nhiều, thu được một thuật toán khá hiệu quả.
¶ Bài tập:
- VNOJ - Minimum Distance
- VNOJ - Dynamic connectivity
- Codeforces 455D - Serega and Fun
- Codeforces 1619H - Permutation and Queries
- VNOJ - Reversals and Sums
- VNOJ - Line queries
- Codeforces 487D - Conveyor Belts
¶ 3. Mở rộng thuật toán Mo
Muc này sẽ trình bày các ứng dụng hiếm gặp hơn của thuật toán Mo. Nếu mới làm quen với chia căn, bạn đọc có thể tạm thời bỏ qua phần này.
¶ 1. Thuật toán Mo có truy vấn cập nhật
¶ Bài toán: VNOJ - Point Update Range Query
Cho mảng gồm phần tử nguyên. Cho truy vấn thuộc một trong hai dạng:
1 i x: Gán .2 l r: Tính tổng các phần tử .
Giới hạn:
¶ Thuật toán Mo
Giả sử bài toán cho chúng ta lần lượt các truy vấn như sau (ta chỉ cần quan tâm đến loại truy vấn là truy vấn gán hay tính tổng):
Truy vấn 1: 2 l r
Truy vấn 2: 1 i x
Truy vấn 3: 2 i x
Truy vấn 4: 1 l r
Truy vấn 5: 1 i x
Truy vấn 6: 2 l r
Tạm thời chỉ quan tâm đến truy vấn tính tổng: Các truy vấn , , và . Giả sử sau khi sắp xếp với thuật toán Mo, các truy vấn có thứ tự xử lí mới là: , , .
Truy vấn có thể được xử lí dễ dàng. Khi đến với truy vấn tiếp theo là , có thể thấy mảng đã bị thay đổi qua các truy vấn cập nhật , , , nên cần tiến hành cập nhật các truy vấn này. Tiếp tục xử lí truy vấn , ta cần phải lần lượt đảo ngược truy vấn cập nhật và .
Có thể thấy thuật toán Mo cũng có thể dùng để giải quyết các bài toán có truy vấn cập nhật. Nhưng nếu sắp xếp truy vấn theo thuật toán Mo bình thường thì tổng số lần cập nhật/đảo ngược giữa các truy vấn có thể rất lớn.
¶ Thuật toán Mo có truy vấn cập nhật
Ta sẽ có cách sắp xếp mới để đảm bảo số lần cập nhật/đảo ngược không quá lớn. Tương tự thuật toán Mo, ta sẽ chia chỉ số liên tiếp vào một nhóm. Ta sắp xếp các truy vấn với các tiêu chí lần lượt như sau:
- Chỉ số nhóm của đầu mút trái.
- Sau đó đến chỉ số nhóm của đầu mút phải.
- Và cuối cùng là số lượng truy vấn cập nhật nằm trước truy vấn này.
struct query{
// t là số lượng truy vấn cập nhật đứng trước truy vấn này
int l, r, t;
int id;
}
bool cmp(const query &a, const query &b){
if(a.l / S != b.l / S)
return a.l < b.l;
else if(a.r / S != b.r / S){
if((a.l / S) % 2 == 1)
return a.r < b.r;
else
return a.r > b.r
}
return a.t < b.t;
}
Phân tích độ phức tạp thuật toán:
- Số lần di chuyển đầu mút trái và phải là có cận trên là .
- Với cách sắp xếp như trên, ta xét những truy vấn có đầu mút trái nằm trong cùng một nhóm, đồng thời đầu mút phải cũng nằm cùng một nhóm, chúng có thứ tự được sắp xếp tăng dần theo . Vậy nên xử lí các truy vấn trong cùng một nhóm sẽ cần tối đa thao tác cập nhật/đảo ngược, khi chuyển nhóm sẽ cần tối đa thao tác cập nhật/đảo ngược khi thay đổi nhóm, vậy cần tối đa thao tác để xử lí các truy vấn cập nhật/đảo ngược. Có thay đổi luân phiên thứ tự sắp xếp như sắp xếp đầu mút phải để giảm số thao tác về .
- Nếu chọn , ta thu được thuật toán có độ phức tạp .
¶ Cài đặt
Cách cài đặt tương đối giống với cài đặt thuật toán Mo bình thường, chỉ cần thêm thao tác xử lí các truy vấn cập nhật.
const int maxN = 2e5 + 5;
struct query{
int l, r, t, id;
}
// Lưu lại thông tin cập nhật: Sau khi thực hiện truy vấn này, a[index] = old sẽ trở thành a[index] = next. Lưu lại như vậy nhằm mục đích thuận tiện khi đảo ngược truy vấn.
struct update{
int index, old, next;
};
vector<update> update_queries;
vector<query> queries;
int n, q;
int a[maxN], b[maxN], ans[maxN];
int S = 0;
int l = 0, r = -1, t = -1;
bool cmp(const query &a, const query &b){
if(a.l / S != b.l / S)
return a.l < b.l;
else if(a.r / S != b.r / S){
if((a.l / S) % 2 == 1)
return a.r < b.r;
else
return a.r > b.r
}
return a.t < b.t;
}
void run_update(int i, int x){
// Nếu i nằm trong [l, r], việc cập nhật sẽ ảnh hưởng đến đáp án
if(l <= i && i <= r){
sum -= a[i];
sum += x;
}
a[i] = x;
}
signed main(){
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n >> q;
for(int i = 1; i <= n; i++){
cin >> a[i];
b[i] = a[i];
}
S = pow(n, 2. / 3.) + 1;
for(int i = 1; i <= q; i++){
int t, u, v;
cin >> t >> u >> v;
if(t == 1){
update_queries.push_back({u, b[u], v});
b[u] = v;
}else{
queries.push_back({u, v, (int)update_queries.size() - 1, i});
}
}
sort(queries.begin(), queries.end(), cmp);
for(query &q : queries){
// Truy vấn cập nhật
while(t < q.t) t++, run_update(update_queries[t].index, update_queries[t].next);
// Đảo ngược truy vấn cập nhật
while(t > q.t) run_update(update_queries[t].index, update_queries[t].old), t--;
while (l > q.l) sum += a[--l];
while (r < q.r) sum += a[++r];
while (l < q.l) sum -= a[l++];
while (r > q.r) sum -= a[r--];
ans[q.id] = sum;
}
}
¶ Bài tập
¶ 2. Thuật toán Mo trên cây
¶ Bài toán: SPOJ COT2 - Count on a tree 2
Cho một cây có đỉnh. Trên mỗi đỉnh gán giá trị . Cho truy vấn có dạng , hãy đếm số lượng giá trị khác nhau nằm trên đường đi từ đỉnh đến đỉnh .
¶ Euler tour
Trước khi đến với thuật toán Mo trên cây, bạn đọc cần nắm rõ về Euler tour. Nếu bài toàn yêu cầu truy vấn trên cây con, ta có thể dễ dàng trải phẳng cây con đó thành một đoạn liên tiếp trên mảng với Euler tour, từ đó áp dụng trực tiếp thuật toán Mo. Xử lí truy vấn đường đi sẽ cần áp dụng khác một chút.
Để phục vụ cho phần trình bày thuật toán bên dưới, ta vẫn nhắc lại một số định nghĩa.
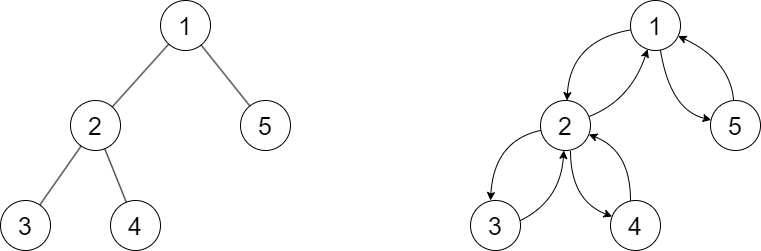
Với là thời điểm bắt đầu duyệt DFS cây con gốc và là thời điểm hoàn thành duyệt cây con gốc . Ta có thứ tự:
¶ Thuật toán Mo trên cây
Ta có một tính chất quan trọng: Nếu nằm trong cây con gốc thì .
Để xử lí truy vấn đường đi từ đến , gọi là tổ tiên chung gần nhất (LCA) của và . Không mất tính tổng quát, giả sử . Xét các đỉnh nằm trên đường đi từ đến :
¶ Trường hợp 1:
Dễ thấy phải nằm trong cây con gốc , đồng thời cũng phải nằm trong cây con gốc . Từ nhận xét ở trên ta thu được:
Từ đây có thể thấy rằng, nếu xét đoạn trên thứ tự thì các đỉnh nằm trên đường đi từ đến chỉ xuất hiện đúng một lần ở vị trí .
¶ Trường hợp 2:
-
Trường hợp 2.1: Đỉnh là tổ tiên của và .
- .
- Do , thời điểm duyệt xong cây con gốc , ta chắc chắn chưa duyệt đến đỉnh nên .
- Từ đây suy ra .
-
Trường hợp 2.2: Đỉnh là tổ tiên của và .
- Do , thời điểm duyệt đến đỉnh thì chắc chắn đã duyệt xong cây con gốc nên .
- Từ đây suy ra .
-
Kết hợp hai trường hợp, ta sẽ có được đoạn cần xét là , trên thứ tự thì đỉnh xuất hiện một lần ở vị trí trong trường hợp 2.1, và ở trong trường hợp 2.2. Với đỉnh , dễ thấy nên đỉnh không xuất hiện lần nào trong đoạn này, vì vậy cần xét riêng đỉnh .
Bây giờ ta đã ánh xạ được các truy vấn về một đoạn liên tiếp trên . Những đỉnh trên đường đi từ đến sẽ xuất hiện một lần trong đoạn này. Khi cài đặt thuật toán Mo, lúc thêm/xóa các đỉnh, ta dễ dàng có thể kiểm soát số lượng của các đỉnh để biết đỉnh nào đang nằm trên đường đi.
¶ Bài tập
- Codeforces 100962F
- VNOJ - Primitive queries: Bài toán áp dụng cả thuật toán Mo có truy vấn cập nhật.
¶ 3. Bỏ trong thuật toán Mo
Các bài toán sử dụng thuật toán Mo thường được kết hợp với các cấu trúc dữ liệu. Việc lựa chọn cấu trúc dữ liệu phù hợp sẽ ảnh hưởng rất nhiều đến độ phức tạp cuối cùng của lời giải.
¶ Bài toán
Cho mảng gồm phần tử. Cho truy vấn dạng , hãy tìm MEX của . Có thể trả lời các truy vấn offline.
Giới hạn:
- .
- .
¶ Thuật toán Mo
Ta sẽ lưu một tập hợp (có thể cài dặt bằng std::set) những giá trị hiện đang không tồn tại trong đoạn đang xét. Đồng thời sẽ sử dụng thêm một mảng đếm để đếm số lượng của mỗi giá trị để thêm xóa tập hợp cho phù hợp.
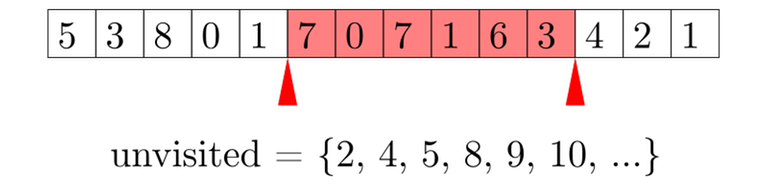
Nguồn: Codeforces
Do sử dụng std::set nên thuật toán có độ phức tạp , tương đối tệ. Phân tích kĩ hơn:
- Thêm một phần tử: Độ phức tạp , thực hiện lần.
- Xóa một phần tử: Độ phức tạp , thực hiện lần.
- Lấy ra giá trị nhỏ nhất trong
std::set: Độ phức tạp , thực hiện lần.
Có thể thấy các thao tác thêm xóa cần thực hiện nhiều hơn nhưng lại có độ phức tạp lớn hơn, ngược lại thao tác tìm giá trị nhỏ nhất lại chạy rất nhanh trong khi thực hiện rất ít lần.
¶ Cấu trúc dữ liệu chia căn
Ta cần một cấu trúc dữ liệu có độ phức tạp thêm/xóa phần tử nhanh, đổi lại việc truy vấn trên cấu trúc dữ liệu có thể lâu hơn. Cấu trúc dữ liệu chia căn rất phù hợp.
Quan tâm đến các giá trị , chia chúng thành các nhóm mỗi nhóm phần tử. Với mỗi nhóm ta sẽ lưu số lượng giá trị ở trong nhóm này xuất hiện ở đoạn đang xét.
Với thao tác thêm, xóa phần tử, ta chỉ cần cập nhật lại giá trị trong mảng đếm và trong nhóm. Hai thao tác có thể được xử lí trong độ phức tạp .
Với thao tác tìm MEX, duyệt lần lượt qua nhóm và tìm ra nhóm đầu tiên không có đầy đủ các giá trị. Sau đó lại duyệt lần lượt các giá trị trong nhóm này để tìm giá trị không xuất hiện. Thao tác này có độ phức tạp .
Vậy thuật toán mới có độ phức tạp .
¶ Bài tập
- MarisaOJ - Truy vấn đoạn
- Codeforces 940F - Machine Learning: Bài toán áp dụng cả thuật toán Mo có truy vấn cập nhật.
¶ Một số cách tối ưu thời gian chạy
¶ Chỉ số nhóm
Rất nhiều bài toán chia căn sẽ sử dụng một hằng số , kích cỡ của một nhóm, block,... và thực hiện rất nhiều phép chia cho . Toán tử chia chạy khá chậm, nên khai báo là biến hằng số bằng từ khóa const trong C++. Phép chia cho biến hằng số được compiler tối ưu rất tốt.
Trường hợp không thể khai biến báo hằng số, có thể tính trước một mảng B[i] = i / S.
¶ Chọn hằng số phù hợp
Việc lựa chọn hằng số phù hợp sẽ ảnh hưởng rất lớn đến độ phức tạp thời gian, không gian. Các bài toán trình bày ở trên hầu hết sẽ được chọn hằng số là hoặc để đỡ rườm rà, nhưng chúng có thể không phải hằng số tối ưu.
Ví dụ ở bài toán Yếu vị được trình bày ở trên, nếu chọn mỗi nhóm có phần tử, thì thao tác khởi tạo có độ phức tạp và thao tác truy vấn có độ phức tạp . Chọn sẽ cho độ phức tạp tốt hơn là .
Tuy nhiên không phải hằng số trên lí thuyết này sẽ cho ra thời gian chạy tốt nhất. Lấy ví dụ bài toán Codeforces 86D - Powerful array được trình bày ở phần thuật toán Mo. Trên lí thuyết việc lựa chọn cho ra độ phức tạp thời gian tốt nhất. Để kiểm chứng, người viết đã sử dụng cùng một code và thử một số hằng số khác nhau, nộp bài sử dụng C++17:
| Thời gian | |
|---|---|
| 2806 ms | |
| 1954 ms | |
| 2058 ms | |
| 2246 ms |
Có thể thấy việc chọn khiến code chạy nhanh hơn đáng kể. Thời gian chạy của code phụ thuộc vào nhiều yếu tố nên khá khó tính được chính xác hằng số phù hợp.
Thay vào đó, ta có thể sinh một số test và chạy thử nghiệm với một vài hằng số khác nhau. Sau đó chọn ra giá trị cho thời gian chạy tốt nhất.
¶ Danh sách bài tập
- VNOJ - Educational SQRT Contest 1
- VNOJ - Educational SQRT Contest 2
- VNOI: Các bài toán chia căn trên Codeforces được phân loại theo cách làm.
- MarisaOJ - Chia căn
- USACO - Square Root Decomposition
¶ Đọc thêm
- Codeforces - An alternative sorting order for Mo's algorithm: Một cách sắp xếp các truy vấn trong thuật toán Mo để tối ưu hóa thời gian.
- https://codeforces.com/blog/entry/68271: Một cách cài đặt thuật toán Mo trên cây khác.
- CP Algorithm - Sqrt tree.