¶ Một số kĩ thuật tối ưu hoá thuật toán Quy Hoạch Động
Tác giả: Lê Anh Đức - A2K42-PBC
Quy hoạch động (QHĐ) là một lớp thuật toán rất quan trọng và có nhiều ứng dụng trong ngành khoa học máy tính. Trong các cuộc thi Olympic tin học hiện đại, QHĐ luôn là một trong những chủ đề chính. Tuy vậy, theo tôi thấy, tài liệu nâng cao về QHĐ bằng tiếng Việt hiện còn cực kỳ khan hiếm, dẫn đến học sinh/sinh viên Việt Nam bị hạn chế khả năng tiếp cận với những kỹ thuật hiện đại. Trong bài viết này, tôi sẽ trình bày một vài kỹ thuật để tối ưu hóa độ phức tạp của một số thuật toán QHĐ.
¶ 1. Đổi biến
Nhiều khi trong trạng thái QHĐ có một thành phần nào đấy với khoảng giá trị quá lớn, trong khi kết quả của hàm lại có khoảng giá trị nhỏ. Trong một vài trường hợp, ta có thể đảo nhãn để giảm số trạng thái.
¶ Bài tập ví dụ
¶ Longest Common Subsequence (LCS)
¶ Đề bài
Cho xâu A độ dài m, xâu B độ dài n. Hãy tìm độ dài xâu con chung dài nhất của hai xâu, chú ý là xâu con chung có thể không liên tiếp.
Giới hạn
- Các kí tự trong cả hai xâu là các chữ cái tiếng Anh in hoa 'A'..'Z'
Ví dụ
A = ADBCC
B = ABCD
LCS = ABC
Kết quả = 3
¶ Lời giải
Thuật toán đơn giản
Gọi là LCS của hai tiền tố và .
Khi đó ta có thể maximize theo và .
Nếu thì ta có thể cập nhật theo .
Kết quả bài toán là .
Độ phức tạp của thuật toán này là , không khả thi với giới hạn của đề bài.
Đổi biến
Đặt
Để ý rằng trong hàm QHĐ trên, các giá trị của sẽ không vượt quá , trong khi đó chiều thứ hai của trạng thái có thể khá lớn (lên tới ).
Để tối ưu hóa, ta sẽ đổi biến. Gọi là vị trí nhỏ nhất sao cho .
Để tính các giá trị của , ta sẽ QHĐ theo kiểu cập nhật đi, thay vì đi tìm công thức trực tiếp cho các .
Gọi nhỏ nhất mà (với là một ký tự từ 'A' đến 'Z').
Mảng có thể tính trong .
Như vậy ta có thể tính các giá trị QHĐ như sau:
- Ban đầu khởi tạo các giá trị , .
- For và tăng dần, với mỗi giá trị khác vô cùng:
- Cập nhật theo .
- Gọi là vị trí xuất hiện tiếp theo của trong xâu bắt đầu từ vị trí , tức là .
- Nếu tồn tại , cập nhật theo .
Để tính kết quả, ta sẽ chỉ cần tìm lớn nhất mà tồn tại khác vô cùng.
#include <bits/stdc++.h>
using namespace std;
const int M = 1e6 + 6;
const int N = 5005;
int dp[N][N];
char a[M], b[N];
int nextPos[M][26];
int m, n;
void minimize(int &a, int b) {
if (a == -1 || a > b) a = b;
}
int main() {
cin >> a + 1 >> b + 1;
m = strlen(a + 1); n = strlen(b + 1);
for (int c = 0; c < 26; ++c)
for (int i = m - 1; i >= 0; --i)
nextPos[i][c] = (a[i + 1] - 'A' == c) ? i + 1 : nextPos[i + 1][c];
int maxLength = min(m, n);
memset(dp, -1, sizeof dp);
dp[0][0] = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j <= i; ++j) if (dp[i][j] >= 0) {
minimize(dp[i + 1][j], dp[i][j]);
int new_value = nextPos[dp[i][j]][b[i + 1] - 'A'];
if (new_value > 0)
minimize(dp[i + 1][j + 1], new_value);
}
}
int ans = 0;
for (int j = maxLength; j > 0; --j) {
for (int i = j; i <= n; ++i)
if (dp[i][j] >= 0) ans = j;
if (ans != 0) break;
}
cout << ans << endl;
return 0;
}
¶ Computer (VNOI Marathon 2010)
Problem Link: COMPUTER - VNOJ.
¶ Đề bài
Công ty phần mềm XYZ mới mua x máy tính để bàn và y máy tính xách tay. Giá một máy tính để bàn là a đồng còn giá một máy tính xách tay là b đồng. Để tránh sự thắc mắc giữa các phòng bàn, Tổng giám đốc đã đưa ra cách phân bố các máy tính này về n phòng ban như sau:
- Sắp xếp n phòng ban theo thứ tự về mức độ quan trọng của các phòng ban.
- Tiến hành phân bố các máy tính cho các phòng ban bảo đảm nếu phòng ban i có mức độ quan trọng nhỏ hơn mức độ quan trọng của phòng ban j thì tổng giá trị máy tính được phân bố cho phòng ban i không được vượt quá tổng giá trị máy tính được phân bố cho phòng ban j.
- Phòng ban nhận được tổng giá trị máy tính nhỏ nhất là lớn nhất.
Là một lập trình viên giỏi nhưng lại thuộc phòng ban có mức độ quan trọng nhỏ nhất, Thắng muốn chứng tỏ tay nghề của mình với đồng nghiệp nên đã lập trình tính ra ngay được tổng giá trị máy trình mà phòng ban mình nhận được rồi mời bạn tính lại thử xem!
Yêu cầu
Cho . Hãy tính tổng giá trị máy tính mà phòng Thắng nhận được.
Input
không quá
Ví dụ
Input
3 300 2 500 2
Output
900
Input
4 300 3 500 2
Output
1300
¶ Lời giải
Trước hết ta sẽ chặt nhị phân kết quả bài toán. Với mỗi giá trị chặt nhị phân, ta cần kiểm tra xem có tồn tại phương án thỏa mãn hay không.
Thuật toán sơ khai
Đặt giá trị cần kiểm tra là v.
Xét các phòng ban theo thứ tự tăng dần về mức độ quan trọng, đánh số từ 1.
Sử dụng một mảng đa chiều để đánh dấu các trạng thái có thể đạt tới. Các giá trị cần quản lí là: chỉ số của phòng ban, đã dùng số máy tính để bàn x, đã dùng số máy tính xách tay y, tổng giá trị máy tính của phòng ban trước đó.
Bắt đầu từ trạng thái (0, 0, 0, 0), ta sử dụng thuật toán loang (BFS). Cuối cùng nếu trạng thái (n, 0, 0, ...) có thể đến được, thì ta sẽ có cách phân hoạch các máy tính vào các phòng ban ứng với giá trị cận dưới v.
Không cần tính toán cụ thể cũng có thể thấy thuật toán này không thể đáp ứng về mặt thời gian (và bộ nhớ) với giới hạn của đề bài.
Nâng cấp bằng nhận xét
Nhận xét rằng ta không cần quan tâm tới thứ tự về mức độ quan trọng của các phòng ban. Với một cách phân hoạch các máy tính sao cho mỗi phòng nhận được tổng giá trị không nhỏ hơn v, ta luôn có thể sắp xếp các bộ theo giá trị không giảm ứng với các phòng ban.
Ta có trạng thái QHĐ là nếu có thể phân bổ máy tính cho i phòng ban, đã dùng x máy tính để bàn và y máy tính xách tay, đã gom được tổng giá trị v cho phòng thứ . Cách làm này số trạng thái vẫn như trước nhưng ta đã có thể chuyển trạng thái trong . Cụ thể từ ta chuyển đến hoặc , chú ý là chỉ có thể dùng thêm máy xách tay nếu và dùng thêm máy để bàn nếu , đồng thời nếu giá trị value đủ lớn hơn hoặc bằng v thì ta chuyển sang trạng thái luôn.
Đổi biến
Ở bài này, ta có thể dễ dàng đổi biến value ra làm hàm mục tiêu. Nhưng không chỉ có vậy, ta có thể đẩy cả i ra ngoài! Cụ thể, = một cặp số lần lượt là số phòng phân bố được và số tiền gom được. Hàm mục tiêu của là một cặp số hoàn toàn có thể so sánh được, trong đó giá trị đầu (i) được ưu tiên so sánh trước.
Cách cập nhật các giống như phần trước, độ phức tạp vẫn là O(1) cho bước chuyển trạng thái, trong khi số trạng thái lúc này là đủ nhỏ đối với giới hạn của đề bài.
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int x, y, a, b, n;
pair<int, int> F[N][N];
pair<int, int> newState(pair<int, int> s, int a, int v) {
s.second += a;
if (s.second >= v) {
++s.first;
s.second = 0;
}
return s;
}
bool dp(int value) {
for (int i = 0; i <= x; ++i) for (int j = 0; j <= y; ++j)
F[i][j] = make_pair(0, 0);
for (int i = 0; i <= x; ++i) for (int j = 0; j <= y; ++j) {
if (F[i][j].first == n) return 1;
if (i < x)
F[i + 1][j] = max(F[i + 1][j], newState(F[i][j], a, value));
if (j < y)
F[i][j + 1] = max(F[i][j + 1], newState(F[i][j], b, value));
}
return 0;
}
int solve() {
int l = 0, r = (a * x + b * y) / n;
int ans = 0;
while (l <= r) {
int mid = l + r >> 1;
if (dp(mid)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
int main() {
cin >> x >> a >> y >> b >> n;
cout << solve() << endl;
cin >> x >> a >> y >> b >> n;
cout << solve() << endl;
return 0;
}
¶ Bài luyện tập
¶ 2. Chia để trị
Đây là kỹ thuật khá hiếm gặp, tuy nhiên lại cực kỳ mạnh.
¶ Bài tập ví dụ
¶ Hai nhà máy CEOI 2004
¶ Đề bài
Có cây cổ thụ được trồng trên một con đường từ đỉnh đổi đến chân đồi. Chính phủ địa phương quyết định cắt bỏ chúng. Để tránh hoang phí, mỗi cái cây cần được chuyển đến một nhà máy cưa.
Cây chỉ có thể được vận chuyển theo một chiều duy nhất: hướng về chân đồi. Có một nhà máy cưa ở cuối con đường. Hai nhà máy cưa có thể được xây dựng dọc theo con đường. Hãy xác định vị trí tối ưu để xây dựng chúng, để cực tiểu hóa chi phí vận chuyển. Chi phí vận chuyển 1kg gỗ đi 1 mét là 1 cent.
Yêu cầu
Viết chương trình:
- đọc dữ liệu từ đầu vào chuẩn số lượng cây, khối lượng và vị trí của chúng,
- tính toán chi phí vận chuyển tối ưu nhất,
- xuất kết quả ra đầu ra chuẩn.
Input
Dòng đầu tiên chứa số - số lượng cây . Các cây được đánh số , theo chiều từ đỉnh đồi đến chân đồi.
dòng tiếp theo mỗi dòng chứa hai số nguyên dương cách nhau bởi dấu cách. Dòng thứ chứa - khối lượng tính theo kg của cái cây thử i và - khoảng cách tính theo mét giữa cây thứ i và cây , . Số cuối cùng, là khoảng cách từ cây thứ n đến chân đồi.
Dữ liệu vào đảm bảo kết quả của bài toán không vượt quá cent.
Output
Một dòng duy nhất chứa một số là kết quả bài toán: chi phí vận chuyển nhỏ nhất.
Ví dụ
Input
9
1 2
2 1
3 3
1 1
3 2
1 6
2 1
1 2
1 1
Output
26
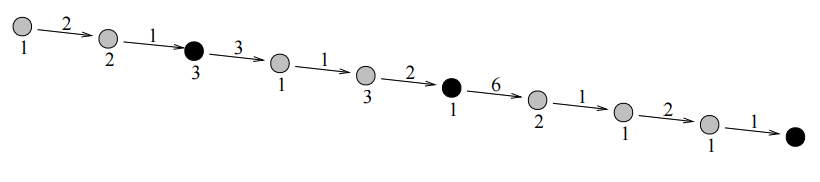
Hình vẽ trên minh họa cho test ví dụ. Các hình tròn được tô đen là các vị trí có nhà máy. Kết quả sẽ là:
.
¶ Lời giải
Trước hết ta sẽ giải quyết vấn đề tính chi phí vận chuyển nếu biết vị trí của hai nhà máy đặt thêm.
Nếu ta có thể tính được chi phí này trong , bài toán sẽ có thể giải được trong - ta có thể for hết các cặp vị trí có thể đặt nhà máy.
Gọi:
- là tổng của các với .
- là tổng của các với .
- là tổng của các với .
Khi đó là chi phí vận chuyển các cây có chỉ số trong đoạn đến nhà máy đặt ở là: .
Như vậy ta có thể xây dựng hàm = chi phí nếu đặt thêm hai nhà máy ở i và j = .
Tuy nhiên lời giải là chưa đủ tốt để có thể giải quyết trọn vẹn bài toán này.
Gọi là vị trí tốt nhất nếu ta đã đặt một nhà máy ở i.
Như vậy kết quả của bài toán sẽ là với .
Nhận xét:
- . Có thể viết tường minh công thức để chứng minh.
- Ta có thể tính các theo thứ tự bất kỳ. Vì các giá trị không liên quan đến nhau nên VD ta có thể tính rồi và .
Như vậy ta có thuật toán sử dụng tư tưởng chia để trị như sau:
Hàm sẽ đi tính các , biết rằng chúng nằm trong đoạn .
void solve(int L, int R, int from, int to) {
if (L > R) return;
int mid = L + R >> 1;
best[mid] = from;
for (int i = from + 1; i <= to; ++i)
if (eval(mid + 1, best[mid]) > eval(mid + 1, i))
best[mid] = i;
solve(L, mid - 1, from, best[mid]);
solve(mid + 1, R, best[mid], to);
}
Đánh giá độ phức tạp thuật toán: vì mỗi lần gọi để quy khoảng được chia đôi, nên sẽ có tầng, mỗi tầng vòng for chỉ chạy qua phần tử, vì vậy độ phức tạp của thuật toán là .
¶ SEQPART - Hackerrank
¶ Đề bài
Cho dãy số , cần chia dãy này thành đoạn liên tiếp. Với phần tử thứ , ta định nghĩa chi phí của nó là tích của và số lượng số nằm cùng đoạn liên tiếp với nó. Chi phí của dãy số ứng với một cách phân hoạch là tổng các chi phí của các phần tử.
Hãy xác định cách phân hoạch dãy số để chi phí là nhỏ nhất.
Input
- Dòng đầu tiên chứa 2 số và .
- dòng tiếp theo, chứa giá trị của dãy .
Output
- Một dòng duy nhất chứa chi phí nhỏ nhất.
Giới hạn
- .
- .
- .
Ví dụ
Input
6 3
11
11
11
24
26
100
Output
299
Giải thích: cách tối ưu là .
Chi phí là .
¶ Lời giải
Đây là dạng bài toán phân hoạch dãy số có thể dễ dàng giải bài QHĐ. Gọi là chi phí nhỏ nhất nếu ta phân hoạch phần tử đầu tiên thành nhóm, khi đó kết quả bài toán sẽ là .
Để tìm công thức truy hồi cho hàm , ta sẽ quan tâm đến nhóm cuối cùng. Coi phần tử 0 là phần tử cầm canh ở trước phần tử thứ nhất, thì người cuối cùng không thuộc nhóm cuối có chỉ số trong đoạn . Giả sử đó là người với chỉ số k, thì chi phí của cách phân hoạch sẽ là , với là chi phí nếu phân người có chỉ số vào một nhóm. Như vậy:
với .
Chú ý là công thức này chỉ được áp dụng với , nếu , đây là trường hợp cơ sở.
Việc cài đặt chỉ đơn giản là dựng mảng 2 chiều , code như sau:
#include <iostream>
using namespace std;
const int MAXL = 8008;
const int MAXG = 808;
const long long INF = (long long)1e18;
long long C[MAXL];
long long sum[MAXL];
long long F[MAXG][MAXL];
long long cost(int i, int j) {
return (sum[j] - sum[i - 1]) * (j - i + 1);
}
int main() {
int G, L;
cin >> L >> G;
for (int i = 1; i <= L; ++i) {
cin >> C[i];
sum[i] = sum[i - 1] + C[i];
}
for (int g = 1; g <= G; ++g) {
for (int i = 0; i <= L; ++i) {
if (g == 1) {
F[g][i] = cost(1, i);
} else {
F[g][i] = INF;
for (int k = 0; k <= i; ++k) {
long long new_cost = F[g - 1][k] + cost(k + 1, i);
if (F[g][i] > new_cost) F[g][i] = new_cost;
}
}
}
}
cout << F[G][L] << endl;
return 0;
}
Chú ý là ta sử dụng mảng tiền xử lí để có thể truy vấn tổng một đoạn (dùng ở hàm ) trong . Như vậy độ phức tạp của thuật toán này là .
Thuật toán tối ưu hơn
Gọi là k nhỏ nhất để cực tiểu hóa , nói cách khác, là k nhỏ nhất mà .
Tính chất quan trọng để có thể tối ưu thuật toán trên là dựa vào tính đơn điệu của , cụ thể:
Ta sẽ không chứng minh điều này ở đây, độc giả có thể tự thuyết phục rằng điều này là đúng.
Chia để trị
Để ý rằng để tính , ta chỉ cần quan tâm tới hàng trước của ma trận:
.
Như vậy, ta có thể tính hàng theo thứ tự bất kỳ.
Ý tưởng là với hàng , trước hết ta tính và với , sau đó sử dụng tính chất nêu trên với và với để đi gọi đệ quy đi tính hai nửa còn lại.
#include <iostream>
const int MAXL = 8008;
const int MAXG = 808;
const long long INF = (long long)1e18;
using namespace std;
long long F[MAXG][MAXL], sum[MAXL], C[MAXL];
int P[MAXG][MAXL];
long long cost(int i, int j) {
if (i > j) return 0;
return (sum[j] - sum[i - 1]) * (j - i + 1);
}
void solve(int g, int L, int R, int optL, int optR) {
if (L > R) return;
int mid = (L + R) / 2;
F[g][mid] = INF;
for (int i = optL; i <= optR; ++i) {
long long new_cost = F[g - 1][i] + cost(i + 1, mid);
if (F[g][mid] > new_cost) {
F[g][mid] = new_cost;
P[g][mid] = i;
}
}
solve(g, L, mid - 1, optL, P[g][mid]);
solve(g, mid + 1, R, P[g][mid], optR);
}
int main() {
int G, L;
cin >> L >> G;
for (int i = 1; i <= L; ++i) {
cin >> C[i];
sum[i] = sum[i - 1] + C[i];
}
for (int i = 1; i <= L; ++i) F[1][i] = cost(1, i);
for (int g = 2; g <= G; ++g) solve(g, 1, L, 1, L);
cout << F[G][L] << endl;
return 0;
}
Chú ý rằng ta không thể đảm bảo rằng chia đôi đoạn , thực tế một vài hàm sẽ chạy chậm hơn nhiều hàm khác.
Tuy nhiên ta có thể chứng minh được, xét về tổng thế thuật toán này chạy đủ nhanh. Mỗi lần ta chia đôi đoạn , nên ta sẽ đảm bảo có tối đa tầng đệ quy, như vậy với mỗi hàng , ta chỉ mất để tính. Toàn bộ thuật toán có độ phức tạp là .

¶ Điều kiện để Chia để trị đúng
¶ Điều kiện theo best
Như ở bài Hai nhà máy CEOI 2004:
Nếu , ta có thể sử dụng chia để trị.
¶ Điều kiện theo cost
Nếu hàm cost thoả mãn quadrangle inequalities:
với mọi ,
ta cũng có thể sử dụng QHĐ chia để trị.
¶ Bài luyện tập
¶ 3. Bao lồi đường thẳng
Các bạn có thể đọc thêm về kỹ thuật bao lồi ở link này
¶ 4. Tối ưu bằng stack
Các tính chất của stack cho phép ta xây dựng một số kỹ thuật để tối ưu thuật toán.
¶ Bài tập ví dụ
¶ BLOCKS - IZHO 2014
¶ Đề bài
Cho dãy số nguyên dương .
Xét các chia dãy số thành nhóm sao cho mỗi nhóm chứa một đoạn liên tiếp các phần tử của . Gọi trọng số của một cách chia là tổng các phần tử lớn nhất của mỗi nhóm.
Yêu cầu
Tìm cách chia dãy số thành nhóm sao cho trọng số của cách chia là nhỏ nhất.
Input
- Dòng 1 chứa hai số nguyên dương và ()
- Dòng 2 gồm số nguyên dương
Output
- Gồm một số nguyên duy nhất là trọng số tìm được
Ví dụ
Input
5 1
1 2 3 4 5
Output
5
Input
5 2
1 2 3 4 5
Output
6
Giới hạn
¶ Lời giải
Thuật toán QHĐ cơ sở
Gọi là tổng trọng số nhỏ nhất để chia số đầu tiên của dãy thành nhóm. Công thức truy hồi là với .
Công thức QHĐ này có thể giải trong , tuy nhiên như vậy cũng chưa đạt yêu cầu.
Nâng cấp thuật toán
Ta thấy rằng chi phí chuyển trạng thái của công thức QHĐ trên đang là , ta có thể tập trung để tối ưu hóa điểm này.
Với mỗi vị trí , ta gọi là vị trí lớn nhất thỏa mãn .
Như vậy trong công thức chuyển trạng thái trên, ta không cần phải for vì khi đó ta chuyển trực tiếp .
Giờ ta chỉ cần quan tâm tới các thuộc đoạn . Lúc này , nên ta chỉ cần tìm . Đây là bài toán truy vấn đoạn có thể giải trong mỗi truy vấn. Độ phức tạp bài toán đến đây là .
Ta vẫn có thể tối ưu hơn nữa bằng cách sử dụng stack để hỗ trợ xử lí các truy vấn. Ta duy trì môt stack, mỗi phần tử chứa hai tham số là và . Stack luôn chứa các giảm dần, còn được cập nhật lại để chứa trong đoạn .
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int K = 105;
const int INF = 0x3f3f3f3f;
int a[N];
int L[N], minF[N];
int dp[K][N];
int n, k;
int main() {
cin >> n >> k;
for (int i = 1; i <= n; ++i) cin >> a[i];
memset(dp, 0x3f, sizeof dp);
dp[1][0] = 0;
for (int i = 1; i <= n; ++i) dp[1][i] = max(dp[1][i - 1], a[i]);
for (int i = 2; i <= k; ++i) {
stack<pair<int, int> > S;
for (int j = i; j <= n; ++j) {
int minF = dp[i - 1][j - 1];
while (!S.empty() && a[S.top().second] <= a[j]) {
minF = min(minF, S.top().first);
S.pop();
}
dp[i][j] = min(dp[i][S.empty() ? 0 : S.top().second], minF + a[j]);
S.push(make_pair(minF, j));
}
}
cout << dp[k][n] << endl;
return 0;
}
Ở bài này ta cũng có thể thay thế stack hoàn toàn bằng cấu trúc dữ liệu Left-Right:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int K = 105;
const int INF = 0x3f3f3f3f;
int a[N], L[N], minF[N];
int dp[K][N];
int n, k;
int main() {
cin >> n >> k;
for (int i = 1; i <= n; ++i) cin >> a[i];
memset(dp, 0x3f, sizeof dp);
dp[1][0] = 0;
for (int i = 1; i <= n; ++i) dp[1][i] = max(dp[1][i - 1], a[i]);
for (int i = 1; i <= n; ++i)
for (L[i] = i - 1; L[i] && a[L[i]] <= a[i]; ) L[i] = L[L[i]];
for (int i = 2; i <= k; ++i) {
minF[i - 1] = INF;
for (int j = i; j <= n; ++j) {
minF[j] = dp[i - 1][j - 1];
for (int t = j - 1; t > L[j]; t = L[t])
minF[j] = min(minF[j], minF[t]);
dp[i][j] = min(dp[i][L[j]], minF[j] + a[j]);
}
}
cout << dp[k][n] << endl;
return 0;
}
¶ Đốn cây (Đề thi HSG quốc gia năm 2016)
¶ Đề bài
Hùng đang làm việc trong Công ty cao su X. Công ty có rừng cao su rất rộng, với những hàng cây cao su trồng cách đều thẳng tắp. Theo định kỳ, người ta thường phải chặt hạ cả hàng cây cao su đã hết hạn khai thác để trồng thay thế bằng hàng cây mới. Hùng phát hiện ra một bài toán tin học liên quan đến vấn đề này: Một nhóm công nhân được giao nhiệm vụ chặt hạ hàng cây gồm cây được trồng dọc theo một đường thẳng với khoảng cách cố định giữa hai cây liên tiếp. Nếu các công nhân cưa đổ một cây, họ có thể cho nó đổ về phía bên trái hoặc bên phải dọc theo hàng cây. Một cây khi đổ có thể lật đổ cây khác bị nó rơi vào và có thể làm đổ nhiều cây khác, theo hiệu ứng lan truyền domino. Sau khi khảo sát kỹ, Hùng đã mô tả được hiệu ứng lan truyền domino như sau: Giả sử các cây trên hàng cây được đánh số từ đến , từ trái qua phải và chiều cao của cây là ()
- Nếu cây đổ về bên trái thì tất cả các cây với cũng sẽ đổ;
- Nếu cây đổ về bên phải thì tất cả các cây với cũng sẽ đổ;
- Mỗi cây chỉ đổ một lần về bên trái hoặc bên phải.
Do đó bài toán đặt ra đối với Hùng là: Xác định số lượng nhỏ nhất các cây mà các công nhân cần cưa đổ đảm bảo hạ đổ toàn bộ hàng cây.
Yêu cầu: Giúp Hùng giải quyết bài toán đặt ra.
Dữ liệu
- Dòng đầu tiên ghi số nguyên dương ;
- Dòng thứ hai chứa số nguyên dương được ghi cách nhau bởi dấu cách, mỗi số không vượt quá .
Kết quả
- Dòng đầu tiên ghi số nguyên dương là số lượng cây mà các công nhân cần cưa đổ;
- Dòng thứ hai ghi dãy số nguyên trong đó () là dãy chỉ số của các cây theo thứ tự các công nhân phải lần lượt cưa đổ, là số dương nếu cây cần cho đổ về bên phải và là số âm nếu cây cần cho đổ về bên trái.
Nếu có nhiều cách thì chỉ cần đưa ra một cách tùy ý.
Ví dụ
INPUT
5
1 2 3 1 1
OUTPUT
2
3 -2
Chú ý: Còn một cách đốn cây khác: Cưa hai cây và và đều cho đổ về bên phải.
Ràng buộc
- Có 40% số test ứng với 40% số điểm của bài có .
- Có 40% số test khác ứng với 40% số điểm của bài có .
- Có 20% số test còn lại ứng với 20% số điểm của bài có .
¶ Lời giải
Bước 1: Chuẩn bị
Ta sẽ xây dựng hai mảng và , trong đó là vị trí nhỏ nhất mà bị cây làm đổ nếu đẩy về bên trái, tương tự với .
với
Để tính ta duy trì một chứa các chỉ số tăng dần. Trước khi thêm một cây mới vào, các cây bị nó trực tiếp làm đổ sẽ bị ra, đồng thời ta cập nhật .
Bước 2: Quy hoạch động
Gọi là số cây cần phải đổ nhỏ nhất để các cây có chỉ số đều đổ.
Để tính cần xét 2 trường hợp:
- Nếu ta đẩy cây qua trái:
với - Nếu cây bị đẩy qua phải bởi cây
với và
Có thể dễ dàng tính các trong . Có thể dùng các cấu trúc dữ liệu quản lí đoạn để giảm xuống .
Ta có thể sử dụng để giảm độ phức tạp xuống .
Để xử lí ta có thể sử dụng kỹ thuật tương tự như bài BLOCK đã trình bày, tuy nhiên ta có thể đánh giá để cài đặt được ngắn gọn hơn:
với
(phần chứng minh xin dành lại cho độc giả)
Để xử lí ta sẽ sử dụng một để lưu các vị trí có giảm dần, đồng thời luôn duy trì sao cho giá trị ở của luôn là tốt nhất. Chú ý là với và thì . Như vậy nếu tại mỗi bước ta các vị trí có ra khỏi , thì sẽ luôn duy trì được tính chất của vì lúc này đảm bảo được là nhỏ hơn các đang ở trong , đồng thời nếu không tốt bằng giá trị ở đầu thì ta sẽ không đẩy vào (để đảm bảo giá trị ở luôn là tốt nhất).
#include <bits/stdc++.h>
using namespace std;
const int N = 4e6 + 6;
int n;
int a[N];
int L[N], R[N];
int dp[N], trace[N];
void initialize() {
vector<int> S;
for (int i = 1; i <= n; ++i) {
L[i] = i;
while (!S.empty() && S.back() > i - a[i])
L[i] = min(L[i], L[S.back()]), S.pop_back();
S.push_back(i);
}
S.clear();
for (int i = n; i >= 1; --i) {
R[i] = i;
while (!S.empty() && S.back() < i + a[i])
R[i] = max(R[i], R[S.back()]), S.pop_back();
S.push_back(i);
}
}
void solve() {
for (int i = 1; i <= n; ++i) dp[i] = i, trace[i] = -i;
vector<int> S;
for (int i = 1; i <= n; ++i) {
if (dp[i] > dp[L[i] - 1] + 1) dp[i] = dp[L[i] - 1] + 1, trace[i] = -(L[i]);
while (!S.empty() && R[S.back()] < i) S.pop_back();
if (!S.empty() && dp[i] > dp[S.back() - 1] + 1) {
dp[i] = dp[S.back() - 1] + 1;
trace[i] = S.back();
}
if (S.empty() || (dp[S.back() - 1] > dp[i - 1])) S.push_back(i);
}
cout << dp[n] << endl;
for (int i = n; i; i = abs(trace[i]) - 1)
cout << (trace[i] < 0 ? -i : trace[i]) << ' ';
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
initialize();
solve();
return 0;
}
¶ 5. Quản lí đồ thị hàm quy hoạch động (Slope Trick)
Ở phần này ta hãy xem xét một bài toán cụ thể về ý tưởng quan sát đồ thị của hàm QHĐ để tối ưu độ phức tạp.
¶ Bài tập ví dụ
¶ Biến đổi dãy số
Link: Codeforces
¶ Đề bài
Cho dãy số phần tử. Mỗi phép biến đổi có thể tăng/giảm một phần tử bất kỳ của dãy 1 đơn vị. Hãy tìm số phép biến đổi ít nhất để dãy trở thành dãy tăng.
Input
- Dòng đầu tiên là số tự nhiên . Dòng tiếp theo là số nguyên
Output
- Một dòng duy nhất chứa số phép biến đổi ít nhất.
Giới hạn
¶ Lời giải
Trước hết ta gán với mọi . Bài toán trở thành biến đổi để dãy trở thành dãy không giảm.
Thuật toán QHĐ cơ sở
Đặt số phép biến đổi ít nhất để biến đổi dãy thành dãy không giảm sao cho . Ta có:
- Với :
- Với :
Kết hợp với nhận xét: Luôn tồn tại dãy cuối cùng với số phép biến đổi tối ưu mà chỉ chứa các giá trị có trong dãy ban đầu. Ta có thể giải công thức QHĐ này với độ phức tạp
Quan sát đồ thị của hàm QHĐ
Ở đây là một hàm theo biến . Nhận xét rằng hàm số này không tăng, tức là nó có độ dốc âm tại mọi điểm (ở đây ta coi là “độ dốc” tại điểm ). Để quản lí hàm số này, ta sẽ lưu lại tập hợp những điểm mà tại đó độ dốc của hàm thay đổi, chú ý là nếu độ dốc tại so với độ dốc tại khác nhau bao nhiêu thì ta lưu lại bấy nhiêu lần.
Gọi là vị trí nhỏ nhất mà tại đó đạt giá trị nhỏ nhất, tức là từ thì độ dốc của bằng . Vậy là đáp án của bài toán.
Hãy cố gắng phác họa hàm trên giấy để có thể dễ dàng hình dung phần còn lại của lời giải.
Để cập nhật lại tập hợp thành ta quan tâm tới 2 trường hợp sau:
- : Trường hợp này, dễ thấy dộ dốc của hàm số của tất cả những điểm nhỏ hơn sẽ giảm đi (bởi vì phần này của hàm số được cộng thêm bởi một hàm bậc nhất có độ dốc là ). Đồng thời .
- : Trường hợp này ta cần đẩy vào tập hợp hai lần. Bởi phần hàm số bên trái sẽ có độ dốc giảm đi , trong khi phần từ đến có độ dốc tăng thêm . Để ý là không còn là điểm đầu tiên mà từ đó hàm đạt cực tiểu nữa, ta xóa khỏi tập hợp .
Các thao tác chèn xóa và lấy của tập hợp có thể dễ dàng cài đặt bằng std::multiset
Như vậy độ phức tạp của lời giải trên là .
#include <bits/stdc++.h>
using namespace std;
int main() {
int n; cin >> n;
multiset<int> slope_changing_points;
long long answer = 0;
for (int i = 1; i <= n; ++i) {
int Ai; cin >> Ai;
Ai -= i;
slope_changing_points.insert(Ai);
if (i == 1) continue;
int opt = *slope_changing_points.rbegin();
if (Ai < opt) {
slope_changing_points.erase(--slope_changing_points.end());
slope_changing_points.insert(Ai);
answer += opt - Ai;
}
}
cout << answer << endl;
return 0;
}
¶ Đào vàng
Link: Topcoder SRM 610 Div1.Level3
¶ Đề bài
Mỏ vàng là có thể được coi là một lưới gồm ô vuông. Các hàng được đánh số từ đến , các cột được đánh số từ đến .
Bạn có thể làm việc ở mỏ vàng một vài ngày. Bạn có thể chọn vị trí để đào trong ngày đầu tiên (ngày ). Trong những ngày tiếp theo, bạn có thể giữ nguyên vị trí, hoặc di chuyển đến một ô vuông khác nằm trong giới hạn được mô tả sau đây.
Khi vàng được tìm thấy ở một ô bất kỳ nào đấy, bạn sẽ nhận được lợi nhuận. Tiền lời được tính bằng trừ đi khoảng cách Manhattan từ ô bạn đang đứng đến ô mà vàng được tìm thấy. Cụ thể nếu vàng được tìm thấy ở ô , và bạn đang đứng ở ô , tiền lời bạn nhận được là , trong đó kí hiệu biểu thị giá trị tuyệt đối.
Bạn được cho hai số nguyên và , hai mảng số nguyên và . Với mỗi số hợp lệ, có một mỏ vàng xuất hiện vào ngày thứ , ở ô .
Cuối cùng bạn có 2 mảng số nguyên và . Số phần tử của hai mảng này ít hơn số phần tử của hai mảng trên 1 đơn vị. Hai mảng này thể hiện giới hạn của việc di chuyển của bạn trong ngày. Cụ thể, với mỗi , giữa ngày và , bạn đang ở ô và chỉ đi được đến ô nếu và .
Hãy xác định tổng lợi nhuận cực đại bạn có thể kiếm được nếu lựa chọn tối ưu làm việc tại ô nào trong mỗi ngày.
Input
- Dòng đầu tiên chứa hai số nguyên và .
- Dòng thứ 2 chứa số ngày mà bạn có thể làm việc .
- Dòng thứ 3 chứa số nguyên mô tả mảng .
- Dòng thứ 4 chứa số nguyên mô tả mảng .
Nếu
- Dòng thứ 5 chứa số nguyên mô tả mảng .
- Dòng cuối cùng chứa số nguyên mô tả mảng .
Output
Một số nguyên duy nhất chứa số tiền lớn nhất mà bạn có thể kiếm được.
Giới hạn
Ví dụ
Input
3 3
1
1
1
Output
6
Vàng tìm được ở ô (1, 1). Chiến lược tốt nhất là làm việc tại đó.
Input
3 3
2
0 2
0 2
1
1
Output
10
Vàng sẽ được phát hiện ở ô (0, 0) hôm nay và ô (2, 2) vào ngày mai. Chiến lược là ở ô (0, 0) hôm nay và ở ô (1, 1) vào ngày mai. Lợi nhuận sẽ là 6 + 4 = 10.
Input
4 2
3
1 4 4
1 2 0
1 1
1 1
Output
15
Input
6 6
6
0 2 1 5 6 4
4 3 1 6 2 0
2 3 1 5 6
2 4 0 5 1
Output
63
¶ Lời giải
Trước hết ta tóm tắt lại đề bài. Có ngày ứng với sự kiện. Mỗi ngày vàng được tìm thấy ở các ô được mô tả qua hai mảng và . Ngày đầu tiên bạn có thể đứng ở vị trí bất kỳ, nhưng từ ngày thứ hai chỉ có thể di chuyển đến một số ô trong khoảng xác định qua hai mảng và .
Hàm mục tiêu là , trong đó là vị trí xuất hiện vàng, còn giới hạn di chuyển là theo chiều dọc và theo chiều ngang. Như vậy lời giải của bài toán là độc lập đối với chiều tọa độ. Chỉ cần xem và là các thành phần độc lập của hàm mục tiêu.
Bài toán hai chiều giờ trở thành hai bài toán một chiều: Có điểm ; ở bước đầu tiên ta có thể chọn xuất phát ở điểm bất kỳ, sau sự kiện và bạn ở vị trí , bạn kiếm được và có quyền tăng/giảm một lượng tối đa là , nhưng không được ra ngoài đoạn . Nếu ta giải được bài toán này, ta hoàn toàn có thể giải tương tự bài toán đối với trục .
Thuật toán quy hoạch động cơ sở
Gọi là số tiền lời nhiều nhất có thể có nếu hiện tại đang bắt đầu lượt thứ và đang đứng ở tọa độ .
Nếu , .
Với , ta sẽ lời thêm , và cần phải quyết định xem tiếp theo sẽ đi tới ô nào. Cần chọn một giá trị thỏa mãn và , đồng thời giá trị là lớn nhất. Khi đó .
Độ phức tạp của thuật toán nếu cài đặt thông thường là , có thể tối ưu thành sử dụng deque nhưng vẫn chưa đạt yêu cầu với giới hạn đề bài.
Đồ thị của hàm QHĐ
Ta có thể coi hàm QHĐ ở trên là một hàm nhận là biến. Xét đồ thị của hàm số này. Dễ thấy , đồ thị của hàm số này là một đường thẳng.
Xét hàm số . Đồ thị của nó sẽ có dạng:
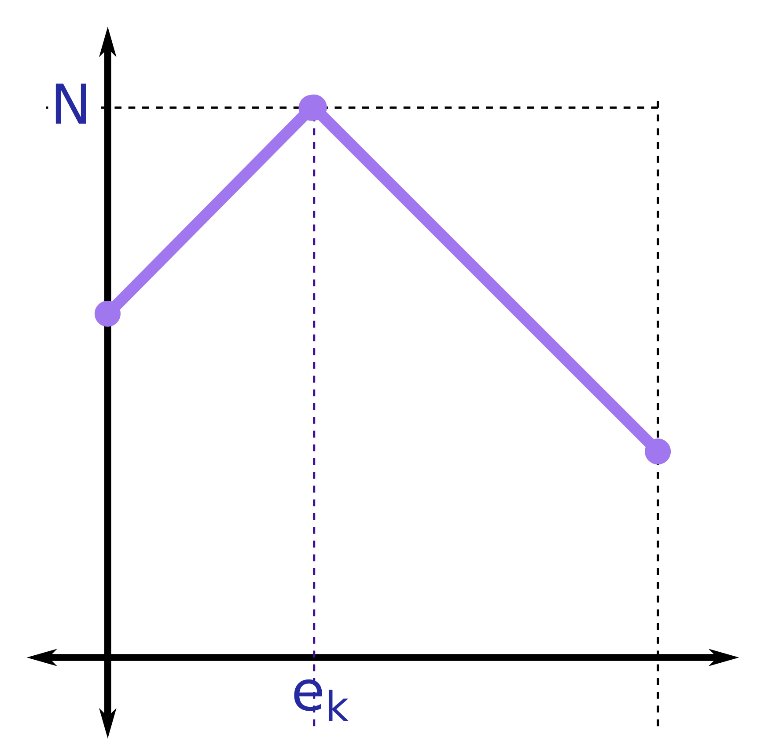
Vấn đề trở nên phức tạp hơn với hàm . Đặt với . Đồ thị của hàm số này có dạng tương tự như đồ thị của hàm số :
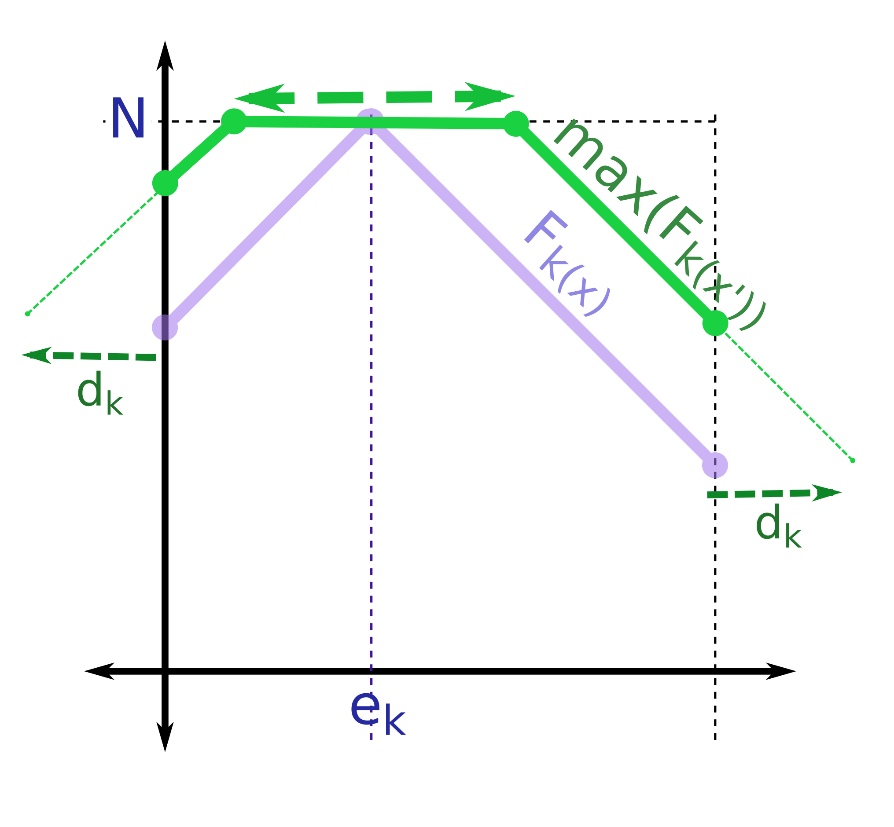
Ta cộng thêm vào hàm , ta sẽ được đồ thị dạng:
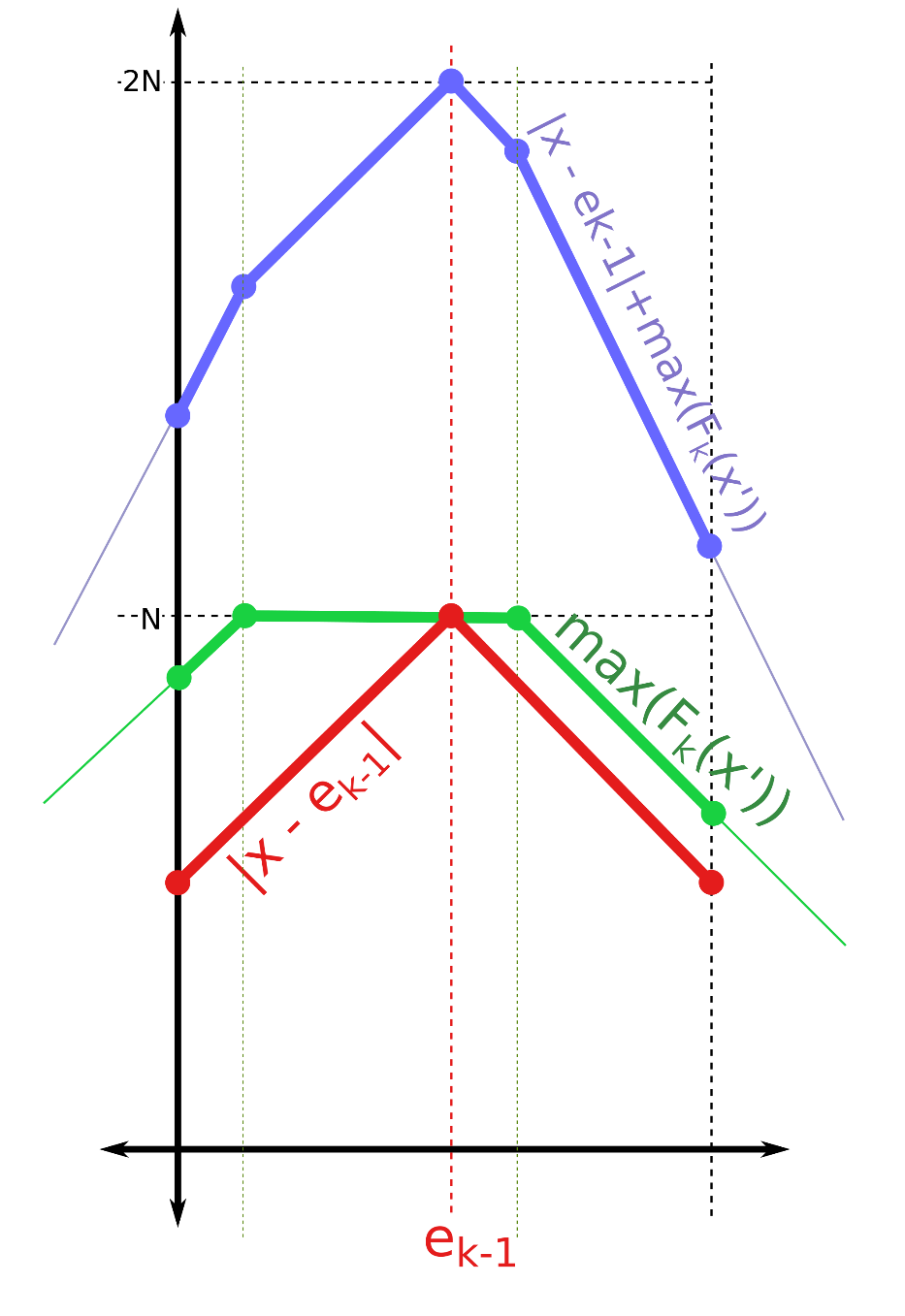
Tương tự như vậy, ý tưởng ở đây là ta sẽ duy trì đồ thị của các hàm số với từ về . Để làm được điều này ta cần phải thực hiện một vài thao tác:
- Tịnh tiến về hai phía: Để tìm được hàm thì trước hết cần xây dựng được hàm . Ta chỉ cần tìm được đỉnh của hàm số, rồi tịnh tiến cả hai phía trái phải của hàm thêm một khoảng .
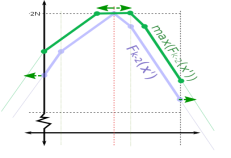
- Tịnh tiến theo trục tung: Ta biểu diễn hàm số bằng danh sách các đỉnh của đường gấp khúc thì thao tác này có thể dễ dàng thực hiện.
Cuối cùng ta chỉ cần chứng minh hàm luôn là hàm lõm thì cách làm trên là đúng. Ban đầu hàm số chỉ là một đường thằng , sau đó ta thực hiện hai thao tác tịnh tiến về hai phía và tịnh tiến theo trục tung . Trong đó chỉ thực hiện được với hàm lõm, và sau thao tác này thì hàm số vẫn là hàm lõm. Với thì ta cộng thêm một hàm lõm (hàm ), mà ta có định lý tổng hai hàm lõm cũng là hàm lõm, nên thao tác này cũng vẫn đảm bảo là hàm lõm.
Độ phức tạp của thuật toán
Ta biểu diễn đồ thị của hàm số bằng danh sách các điểm, sau mỗi thao tác thì số định của đường gấp khúc tăng thêm tối đa là , nên số đỉnh này là một đại lượng . Như vậy độ phức tạp của toàn bộ thuật toán là .
#include <bits/stdc++.h>
using namespace std;
const int INF = 2e9;
void maximize(int &a, int b) {
if (a < b) a = b;
}
struct Point {
long long x, y;
Point(long long x, long long y): x(x), y(y) {}
bool operator < (const Point &o) const {
return x < o.x;
}
};
vector<Point> H;
void incConst(int delta) {
for (int i = 0; i < H.size(); ++i) H[i].y += delta;
}
void expand(int delta) {
int L = 0, R = 0;
for (int i = 1; i < H.size(); ++i) {
if (H[i].y > H[L].y) {
L = R = i;
} else if (H[i].y == H[L].y) {
R = i;
}
}
if (L == R) {
H.insert(H.begin() + L + 1, H[L]);
++R;
}
for (int i = 0; i <= L; ++i) H[i].x -= delta;
for (int i = R; i < H.size(); ++i) H[i].x += delta;
}
int calc(Point P, Point Q, int x) {
if (P.y == Q.y) return P.y;
int diff = P.y - Q.y;
long long y = min(P.y, Q.y);
long long L = x - P.x;
long long R = Q.x - x;
if (L == 0) return P.y;
if (R == 0) return Q.y;
if (diff < 0)
y -= L * diff / (L + R);
else
y += R * diff / (L + R);
return y;
}
int eval(int x) {
for (int i = 0; i + 1 < H.size(); ++i) if (H[i].x <= x && x <= H[i + 1].x)
return calc(H[i], H[i + 1], x);
}
void mergeHull(int v) {
//merge with y = -abs(x - v)
int exist = -1;
for (int i = 0; i < H.size(); ++i) if (H[i].x == v) {
exist = i;
break;
}
if (exist == -1) {
H.push_back(Point(v, eval(v)));
sort(H.begin(), H.end());
}
for (int i = 0; i < H.size(); ++i) H[i].y -= abs(H[i].x - v);
}
int solve(int len, vector<int> pos, vector<int> range) {
H.clear();
int n = pos.size();
H.push_back(Point(0, len - pos[0]));
if (pos[0] != 0) H.push_back(Point(pos[0], len));
if (pos[0] != len) H.push_back(Point(len, len - abs(pos[0] - len)));
for (int i = 1; i < n; ++i) {
expand(range[i - 1]);
mergeHull(pos[i]);
incConst(len);
}
int ans = 0;
int last = 0;
for (int x = 0; x <= len; ++x) {
while (last < H.size() && H[last].x <= x) ++last;
if (last == H.size()) --last;
ans = max(ans, calc(H[last - 1], H[last], x));
}
return ans;
}
int getMaximumGold(int N, int M, vector<int> event_i, vector<int> event_j, vector<int> event_di, vector<int> event_dj) {
return solve(N, event_i, event_di) + solve(M, event_j, event_dj);
}
int main() {
int N, M, D;
cin >> N >> M >> D;
vector<int> event_i(D), event_j(D), event_di(D - 1), event_dj(D - 1);
for (int i = 0; i < D; ++i) cin >> event_i[i];
for (int i = 0; i < D; ++i) cin >> event_j[i];
for (int i = 0; i < D - 1; ++i) cin >> event_di[i];
for (int i = 0; i < D - 1; ++i) cin >> event_dj[i];
cout << getMaximumGold(N, M, event_i, event_j, event_di, event_dj) << endl;
}