¶ Quy hoạch động cái túi (DP Knapsack), phần 2
Tác giả:
- Nguyễn Tấn Minh - Trường Đại học Khoa học Tự nhiên, ĐHQG-HCM.
Reviewer:
- Nguyễn Quang Minh - Michigan State University.
- Võ Khắc Triệu - National University of Singapore.
- Võ Đức Đoàn - THPT Chuyên Nguyễn Tất Thành, Quãng Ngãi.
- Nguyễn Minh Hiển - Trường Đại học Công nghệ, ĐHQGHN.
¶ Giới thiệu
Trong phần 1 của bài viết này, ta đã tìm hiểu một số lời giải cơ bản và phổ biến của hai bài toán 0/1 Knapsack và Subset Sum của lớp bài toán cái túi.
Trong phần này, chúng ta sẽ tìm hiểu thêm hai thuật toán cải tiến các bài toán nêu trên.
¶ Bài toán Subset sum trên tập số nguyên liên tiếp
Khi xử lý bài toán kiểm tra sự tồn tại của một tập con có tổng trên tập số nguyên liên tiếp, ta hoàn toàn có thể dùng thuật toán tham lam để giải trong . Do đó, trong phần này, ta chỉ tập trung vào bài toán đếm số tập con có tổng .
¶ Bài toán không có cận
¶ Đề bài
Cho số nguyên , đếm số tập con của tập số tự nhiên có tổng là .
Giới hạn:
¶ Thuật toán
Nếu áp dụng thuật toán quy hoạch động truyền thống với là số tập con của có tổng là , ta có thuật toán có độ phức tạp với công thức truy hồi là:
Tuy nhiên, với giới hạn , đây rõ ràng là một lời giải chưa tối ưu.
¶ Thay đổi hướng tiếp cận
Đối với các dạng quy hoạch động cái túi được nêu trên, ta có thể hình dung mô hình bài toán đang là tuần tự thêm phần tử vào cuối dãy trạng thái. Nói cách khác, ta mở rộng từ trạng thái sang (với cho biết món đồ thứ được chọn hay không chọn). Tuy nhiên, với bài toán nêu trên, ta có thể tận dụng tính liên tiếp của tập số để tuần tự thêm phần tử vào đầu dãy trạng thái, sau đó đánh số lại toàn bộ dãy.
Ví dụ, với tập ứng với dãy trạng thái . Nếu thêm trạng thái mới vào cuối dãy, ta có:
- Dãy ứng với tập .
- Dãy ứng với tập .
Tuy nhiên, với việc thêm trạng thái mới vào đầu dãy, ta có hai tập mới là và .
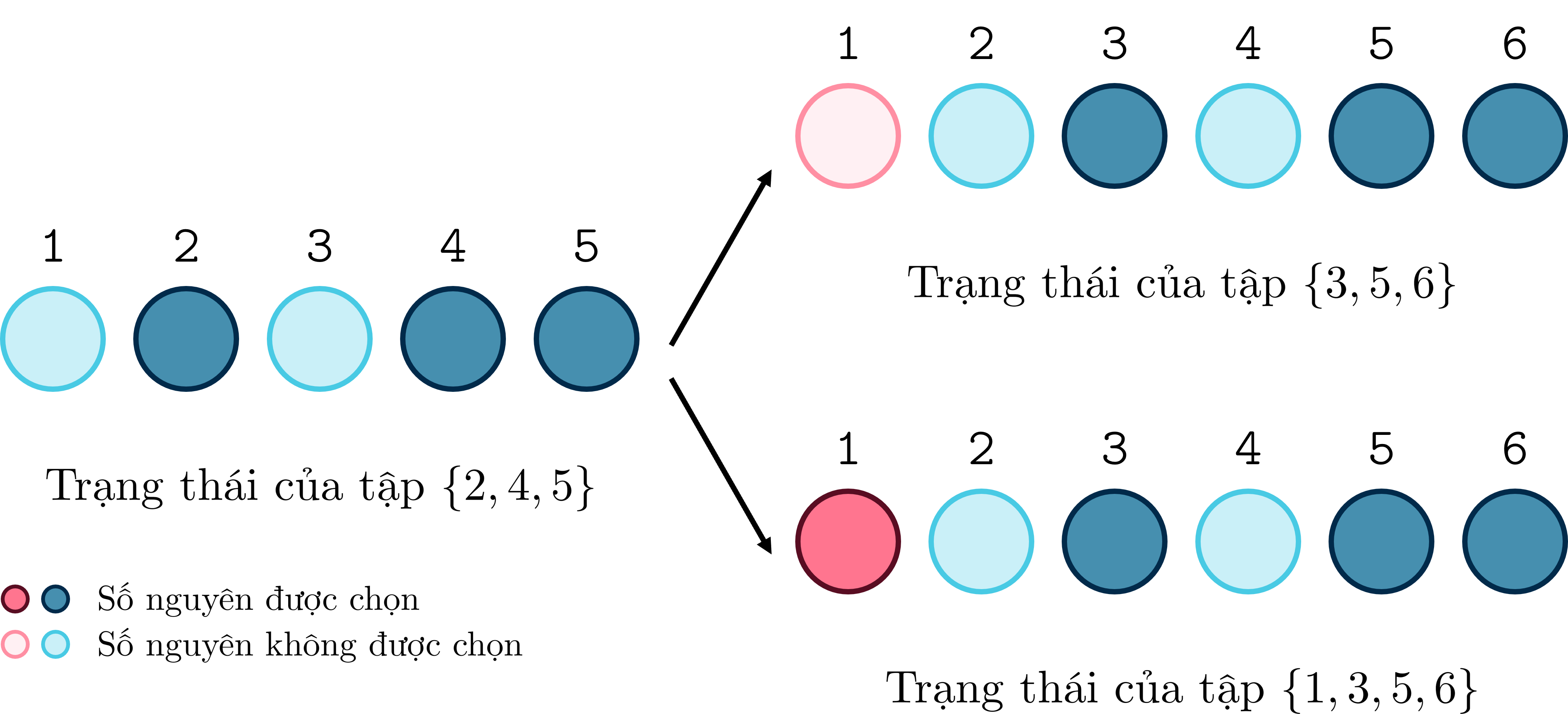
Nói một cách toán học hơn, từ tập , ta sẽ sinh ra tất cả các tập số tự nhiên khác rỗng theo hai thao tác sau:
- Gán , tức thêm trạng thái không chọn vào đầu dãy trạng thái.
- Gán , tức thêm trạng thái chọn vào đầu dãy trạng thái.
Ở đây, ta định nghĩa phép cộng một tập hợp với một số nguyên cho ra tập hợp:
¶ Ý tưởng quy hoạch động
Lúc này, với mọi tập số tự nhiên, ta chỉ cần quan tâm hai tham số là tổng các giá trị thuộc tập (ký hiệu ) và kích thước của tập (ký hiệu ). Khi áp dụng các thao tác nêu trên, hai tham số này thay đổi như sau:
- Khi áp dụng thao tác gán lên các tập có tổng và kích thước , chúng sẽ biến thành các tập có tổng và kích thước . Ví dụ, với tập có tổng và kích thước , thao tác này sẽ tạo ra tập có tổng và kích thước giữ nguyên.
- Khi áp dụng thao tác gán lên các tập có tổng và kích thước , chúng sẽ biến thành các tập có tổng và kích thước . Ví dụ, với tập có tổng và kích thước , thao tác này sẽ tạo ra tập có tổng và kích thước .
Từ đó, ta có thể đặt (với ) là số tập số tự nhiên có tổng giá trị là và kích thước là . Để lập công thức truy hồi, ta có thể suy ngược lại:
- Với các tập không chứa phần tử , ta có tập hợp như vậy.
- Với các tập chứa phần tử , ta có tập hợp như vậy.
Như vậy, ta có:
¶ Độ phức tạp
Thoạt nhìn qua, ta có cảm giác như lời giải này cũng có độ phức tạp như lời giải trước đó. Tuy nhiên, dựa vào nhận xét rằng với mọi tập số nguyên, tổng của nó tối thiểu là , tức là:
Như vậy, kích thước của một tập con không thể vượt quá căn bậc hai của hai lần tổng của nó. Nói cách khác, số trạng thái mà ta cần xét trong thuật toán quy hoạch động này là -- đủ để xử lý giới hạn .
Code tham khảo
Trước tiên, ta khai báo hai hàm giúp tính phép cộng có modulo và kiểm tra tính hợp lệ của một trạng thái như sau:
const int MOD = 1e9 + 7;
int add (int a, int b) {
return a + b - (a + b < MOD ? 0 : MOD);
}
bool validState (int sigma, int len) {
return 1LL * len * len <= 2 * sigma;
}
Sau đó, thuật toán nêu trên có thể được cài đặt như sau:
int C; cin >> C;
vector<vector<int>> dp(C + 1);
dp[1] = {0, 1};
for (int sigma = 2; sigma <= C; sigma++) {
dp[sigma].push_back(0); // phần tử đệm
for (int len = 1; validState(sigma, len); len++) {
int cur = 0;
if (validState(sigma - len, len))
cur = add(cur, dp[sigma - len][len]);
if (validState(sigma - len, len - 1))
cur = add(cur, dp[sigma - len][len - 1]);
dp[sigma].push_back(cur);
}
}
int ans = 0;
for (int len = 1; validState(C, len); len++) ans = add(ans, dp[C][len]);
cout << ans;
¶ Bài toán có cận dưới
¶ Đề bài
Cho hai số nguyên và , đếm số tập con của tập số có tổng là .
Giới hạn:
¶ Ý tưởng
Khi bài toán có cận dưới, ta có thể xử lý theo một trong hai hướng sau:
- Biến đổi thao tác sinh tập số thành và . Sau đó bắt đầu sinh với tập .
- Với tập số có kích thước , ta giảm toàn bộ các phần tử xuống đơn vị. Nói cách khác, ta sử dụng thuật toán không có cận dưới nhưng tìm các tập số có tổng là .
¶ Bài toán có cận trên
¶ Đề bài
Cho hai số nguyên và , đếm số tập con của tập số có tổng là .
Giới hạn:
- .
¶ Ý tưởng
Với việc đặt trạng thái bằng cặp , ta không thể quản lý được giới hạn (cận trên) của tập số đang được tính trong hàm quy hoạch động. Cụ thể, với tập số có chứa , việc áp dụng thao tác sẽ sinh ra tập có chứa phần tử .
Cách giải quyết vấn đề này chính là bù trừ. Giả sử ta có trạng thái đang tính dư các tập chứa phần tử , ta cần trừ đi số tập dư. Mặt khác, ta biết rằng số tập có tổng , kích thước chứa phần tử cũng chính là số tập có tổng , kích thước không chứa phần tử , hay chính là .
Lý do ta chỉ cần bù trừ các tập chứa phần tử là với cách làm như trên, ta luôn duy trì các tập trong khoảng . Trong quá trình thực hiện các thao tác nêu trên, phần tử vượt giới hạn duy nhất được sinh ra là và bị loại ngay lập tức.
Từ đó, ta điều chỉnh công thức truy hồi như sau:
Code tham khảo
Để tiện lợi cho việc bù trừ, ta định nghĩa thêm một hàm tính phép trừ có modulo như sau:
int sub (int a, int b) {
return a - b + (a - b >= 0 ? 0 : MOD);
}
Sau đó, thuật toán nêu trên có thể được cài đặt như sau:
int C, n; cin >> C >> n;
vector<vector<int>> dp(C + 1);
dp[0] = {1}, dp[1] = {0, 1};
for (int sigma = 2; sigma <= C; sigma++) {
dp[sigma].push_back(0); // phần tử đệm
for (int len = 1; validState(sigma, len); len++) {
int cur = 0;
if (validState(sigma - len, len))
cur = add(cur, dp[sigma - len][len]);
if (validState(sigma - len, len - 1))
cur = add(cur, dp[sigma - len][len - 1]);
if (sigma > n && validState(sigma - n - 1, len - 1))
cur = sub(cur, dp[sigma - n - 1][len - 1]);
dp[sigma].push_back(cur);
}
}
int ans = 0;
for (int len = 1; validState(C, len); len++) ans = add(ans, dp[C][len]);
cout << ans;
¶ Thuật toán quy hoạch động của David Pisinger
Năm 1997, David Pisinger đã xuất bản bài báo cáo về thành quả nghiên cứu bài toán cái túi của mình. Trong bài báo cáo ấy, ông đã đề xuất một hướng tiếp cận khác cho QHĐ cái túi, giúp xử lý bài toán Subset sum trong và 0/1 Knapsack trong . Năm 1999, Martello, Pisinger và Toth đã đưa ra nhiều cải tiến quan trọng cho thuật toán 0/1 Knapsack nhưng thuật toán này tương đối phức tạp và không phổ biến trong Lập trình thi đấu.
Độ phức tạp của thuật toán này tốt hơn quy hoạch động truyền thống ở chỗ nó không phụ thuộc vào tổng trọng số cần tìm (trong bài toán Subset Sum) hay giới hạn của cái túi (trong bài toán 0/1 Knapsack). Đây là một cải tiến hữu ích đặc biệt là với các dạng bài có giới hạn lên đến , khi đó độ phức tạp của thuật toán truyền thống tương đương .
Lưu ý
Để thuận lợi cho việc giải thích thuật toán, một số thuật ngữ và cách định nghĩa trong bài viết này sẽ có đôi chút khác biệt so với bài báo cáo của Pisinger. Tuy nhiên, những thay đổi này không làm thay đổi hiệu suất của thuật toán.
¶ Ý tưởng chung
Trong phần này, ta sử dụng một dãy để biểu diễn trạng thái chọn hay không chọn của các món đồ (với ).
Định nghĩa 1. Ta định nghĩa một điểm cắt là chỉ số của món đồ cuối cùng đặt vừa vào túi, nếu ta liên tục lấy các món đồ từ đến hết (tạm thời, ta đang không quan tâm thứ tự của các món đồ). Nói cách khác, ta có:
Bên cạnh đó, ta gọi lời giải tại điểm cắt là phương án chọn tất cả các món đồ từ đến và không chọn các món đồ còn lại. Ngoài ra, từ điểm cắt , ta tách các món đồ thành hai nhóm lần lượt là các món đồ từ đến và từ đến .
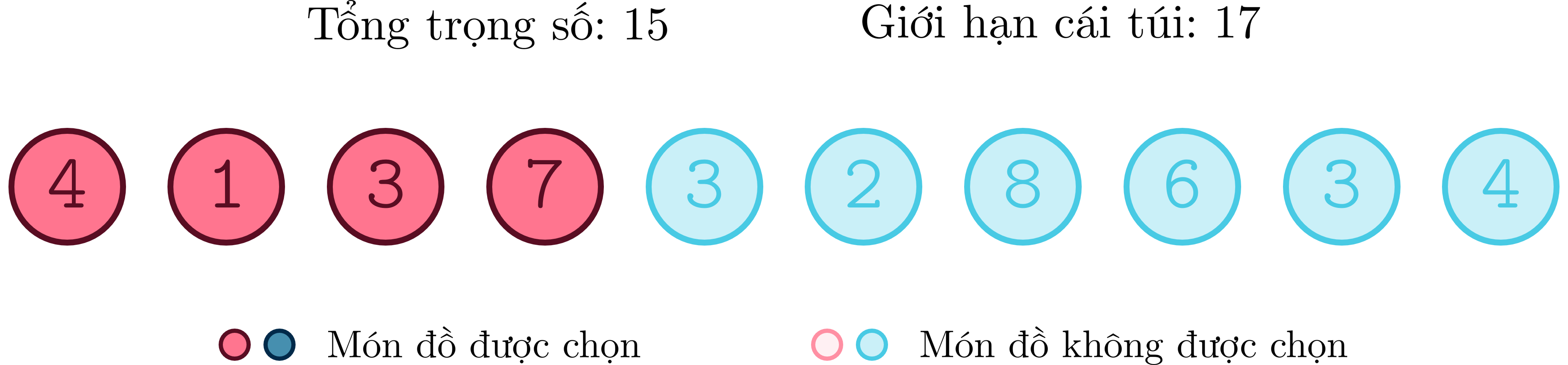
Định nghĩa 2. Ta định nghĩa một trạng thái chọn/không chọn các món đồ là trạng thái cân bằng nếu trạng thái này có thể được biến đổi từ lời giải tại điểm cắt thông qua hai thao tác:
- Xóa món đồ: Khi tổng trọng số của một trạng thái cân bằng lớn hơn , ta có thể bỏ đi một món đồ bất kỳ trong nhóm .
- Thêm món đồ: Khi tổng trọng số của một trạng thái cân bằng không quá , ta có thể chọn thêm một món đồ bất kỳ trong nhóm .
Lưu ý, tại mọi thời điểm, việc chọn loại thao tác để thực hiện phụ thuộc vào tổng trọng số của trạng thái đang xét. Hơn nữa, với định nghĩa như trên, ta đang cho phép tổng trọng số của một số trạng thái vượt quá giới hạn cái túi.
Ví dụ, từ lời giải tại điểm cắt như hình trên, ta có thể thêm một món đồ có trọng số và bỏ đi hai món đồ có trọng số và để cho ra một trạng thái cân bằng như sau:
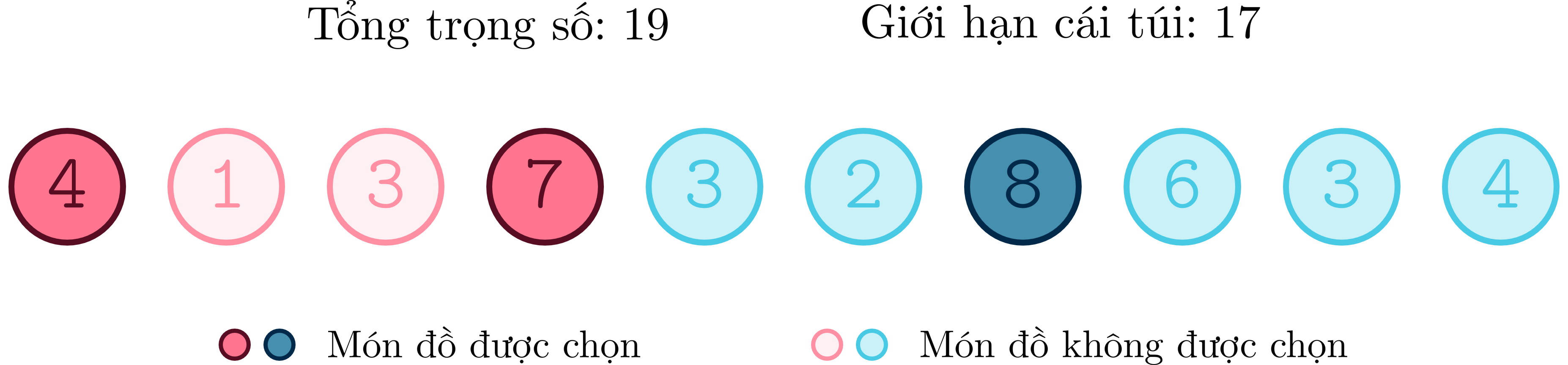
Tính chất 1. Với cách định nghĩa như trên, ta có thể chứng minh rằng mọi lời giải tối ưu/hợp lệ của bài toán 0/1 Knapsack và Subset sum đều là một trạng thái cân bằng.
Chứng minh
Gọi lần lượt là các món đồ cần bỏ đi thuộc nhóm và lần lượt là các món đồ cần thêm vào thuộc nhóm để đạt được lời giải tối ưu.
Với mỗi thao tác xóa, ta chọn một phần tử của , xóa món đồ tương ứng rồi xóa luôn phần tử ra khỏi dãy . Tương tự với thao tác thêm món đồ và dãy .
Với bài toán Subset sum, ta sẽ thực hiện bài toán đến khi:
- Trạng thái đạt được cũng chính là lời giải hợp lệ. Nói cách khác, cả hai dãy đã được xóa hết phần tử.
- Dãy đã được xóa hết phần tử mà tổng trọng số hiện tại lớn hơn . Nói cách khác, lời giải này chắc chắn có tổng trọng số lớn hơn . Điều này vô lý vì lời giải của bài toán Subset sum phải là một tập các món đồ có trọng số đúng bằng .
- Dãy đã được xóa hết phần tử mà tổng trọng số hiện tại không quá . Nói cách khác, lời giải này chắc chắn có tổng trọng số bé hơn . Một lần nữa, điều này lại vô lý vì không thỏa yêu cầu của bài toán.
Lưu ý, khi cả hai dãy chưa được xóa hết phần tử, ta luôn có thể tiếp tục xóa bằng thao tác xóa/thêm món đồ.
Tương tự với bài toán 0/1 Knapsack, ta thực hiện bài toán đến khi:
- Trạng thái đạt được cũng chính là lời giải tối ưu. Nói cách khác, cả hai dãy đã được xóa hết phần tử.
- Dãy đã được xóa hết phần tử mà tổng trọng số hiện tại lớn hơn . Nói cách khác, lời giải này chắc chắn có tổng trọng số lớn hơn . Điều này vô lý vì lời giải của bài toán 0/1 Knapsack phải có tổng trọng số không quá .
- Dãy đã được xóa hết phần tử mà tổng trọng số hiện tại không quá . Nói cách khác, ta đã tìm được một lời giải hợp lệ khác có tập món đồ được chọn là tập cha của tập món đồ được chọn trong lời giải tối ưu. Điều này là vô lý vì lời giải tối ưu phải có tổng giá trị lớn nhất.
Tính chất 2. Tổng trọng số của một trạng thái cân bằng luôn nằm trong khoảng với .
Chứng minh
Ta chỉ có thể đạt được tổng trọng số không quá khi thực hiện thao tác xóa món đồ trên trạng thái có tổng trọng số không quá . Tương tự, ta chỉ có thể đạt được tổng trọng số lớn hơn khi thực hiện thao tác thêm món đồ trên trạng thái có tổng trọng số lớn hơn .
Có thể thấy, ý tưởng của thuật toán quy hoạch động của David Pisinger là duy trì một trạng thái cân bằng có trọng số trong khoảng thay vì xét hết tất cả các trạng thái hợp lệ có trọng số trong khoảng như cách làm truyền thống. Điều này cũng giúp số lượng giá trị tổng trọng số phân biệt cần xét giảm từ xuống .
Đây là đồ thị mô phỏng sự thay đổi của tổng trọng số theo hướng tiếp cận của thuật toán này so với hướng tiếp cận của lời giải quy hoạch động truyền thống:
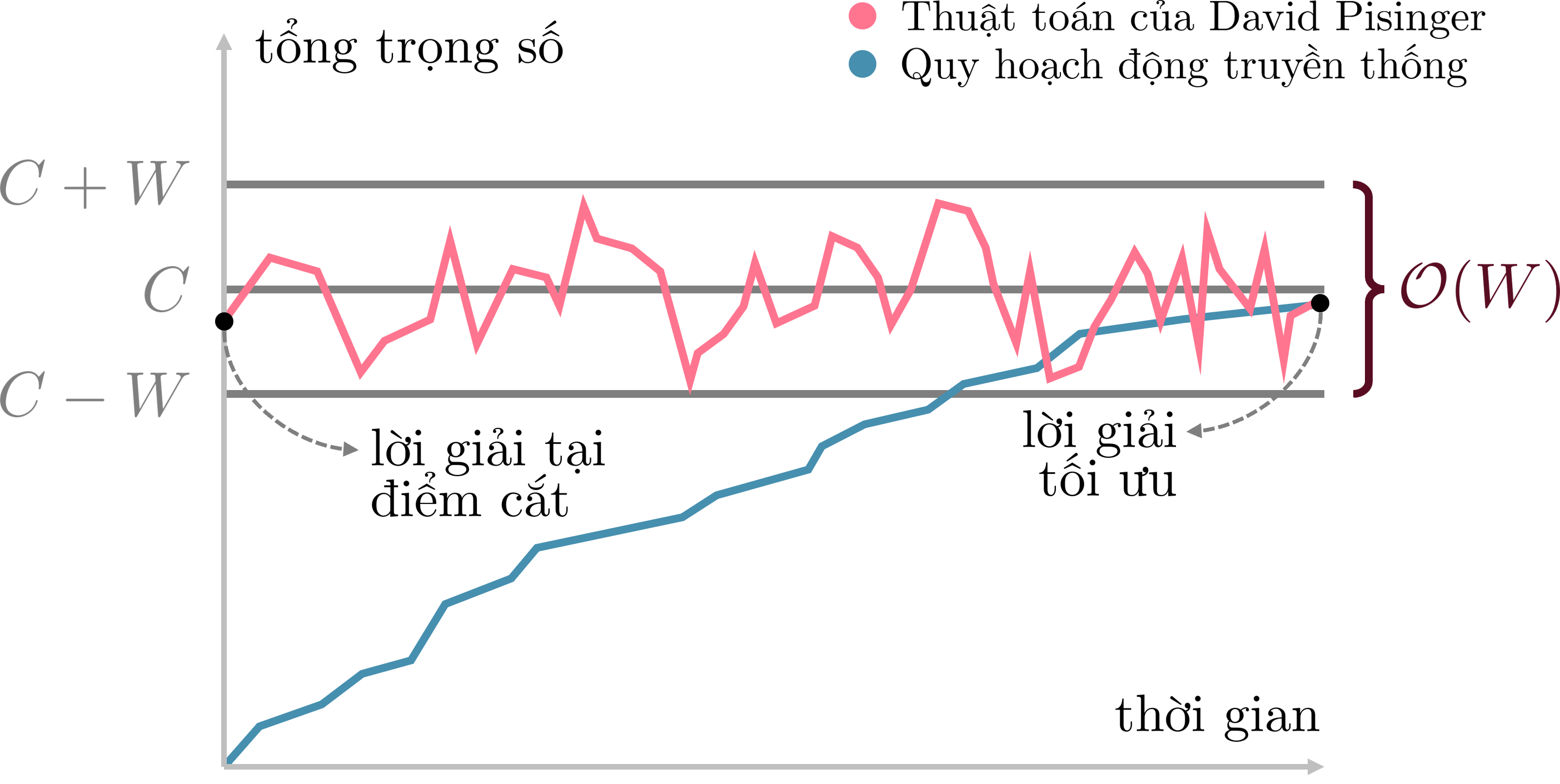
¶ Lời giải cho bài toán Subset sum
¶ Quy hoạch động
Gọi là một giá trị boolean cho biết sự tồn tại của một trạng thái cân bằng có tổng trọng số nếu chỉ áp dụng thao tác xóa món đồ cho phần tử đầu tiên của nhóm và thao tác thêm món đồ cho phần tử đầu tiên của nhóm .
Dễ thấy, nếu hoặc thì cũng phải trả về . Ngoài ra, ta xét thêm hai trường hợp chuyển trạng thái:
- Nếu và , ta có thể xóa phần tử thứ của nhóm , suy ra .
- Nếu và , ta có thể thêm phần tử thứ của nhóm , suy ra .
Từ đó, ta có công thức truy hồi cho như sau:
Lưu ý, khi , chỉ có với là tổng trọng số của lời giải tại điểm cắt.
Code tham khảo
/// tìm điểm cắt
int breakPoint = 0, curSum = 0;
for (int i = 1; i <= n && curSum + w[i] <= C; i++)
curSum += w[i], breakPoint = i;
/// chuẩn bị các tham số liên quan & trường hơp cơ sở
int W = *max_element(w + 1, w + 1 + n), offset = C - W;
exist[0][0][curSum - offset] = 1;
/// thực hiện QHĐ
for (int i = 0; i <= breakPoint; i++) {
for (int j = 0; j <= n - breakPoint; j++) {
for (int sigma = C - W; sigma <= C + W; sigma++) {
int cur = sigma - offset;
if (!exist[i][j][cur]) continue;
if (i < breakPoint) {
exist[i + 1][j][cur] = 1;
if (sigma > C) exist[i + 1][j][cur - w[i + 1]] = 1;
}
if (j < n - breakPoint) {
exist[i][j + 1][cur] = 1;
if (sigma <= C) exist[i][j + 1][cur + w[breakPoint + j + 1]] = 1;
}
}
}
}
cout << exist[breakPoint][n - breakPoint][C - offset];
¶ Quy hoạch động
Khi cố định hai tham số và , ta có hai tính chất sau đây:
Như vậy, với mọi cặp , tồn tại một giá trị thỏa . Nói cách khác, là nhỏ nhất thỏa , ta gọi giá trị này là . Trong trường hợp không tồn tại thỏa mãn, ta quy ước .
Không khó để chứng minh khi cố định thì là hàm nghịch biến (tức tăng thì giảm).
Từ công thức truy hồi cho ở lời giải , ta thấy, khi một trạng thái có , nó sẽ kéo theo:
- .
- .
- , nếu .
- , nếu .
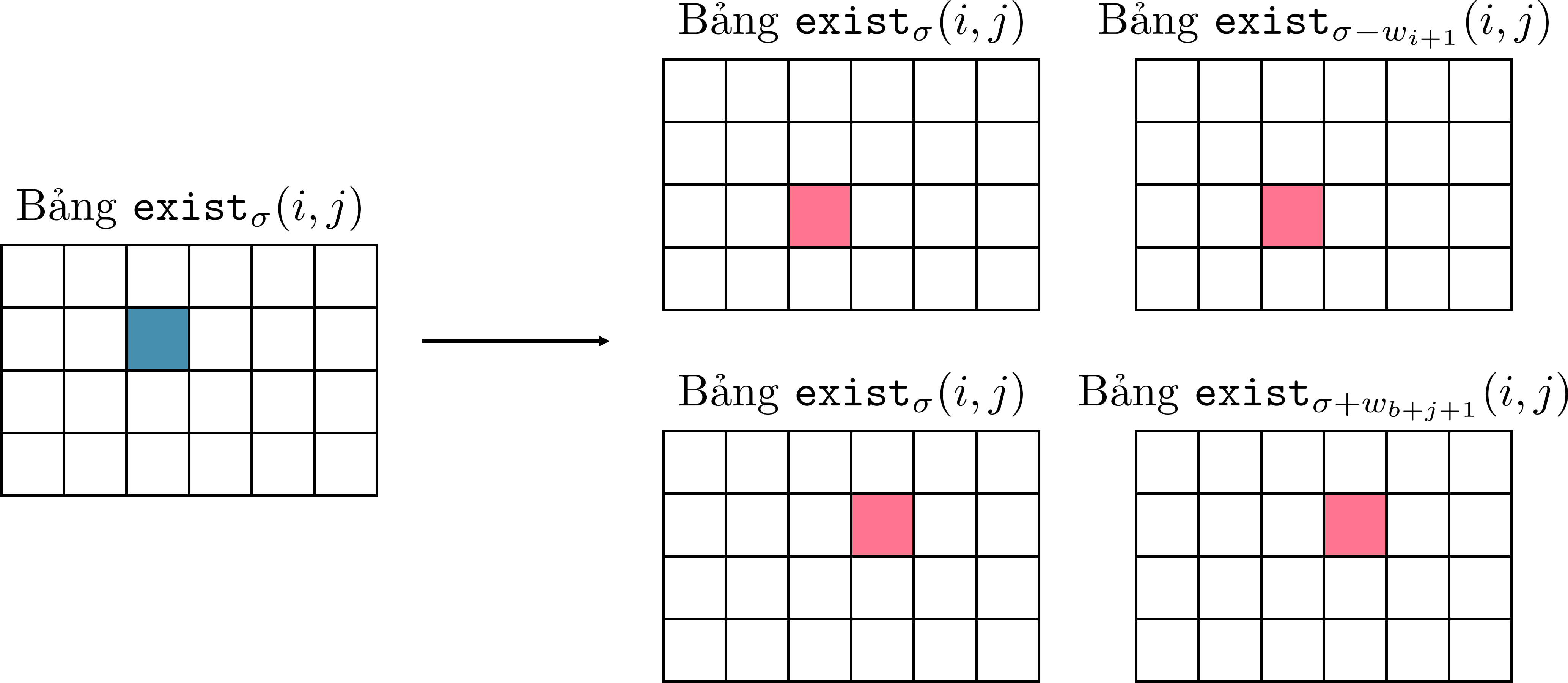
Từ đó, nếu cố định và cùng lúc các vị trí với , nó sẽ kéo theo:
- với .
- với , nếu .
- , với , nếu .
Ở hai trường hợp đầu tiên, ta đều có các trạng thái thái di động theo tham số , hai tham số và được cố định cùng một giá trị. Tuy nhiên, ở trường hợp cuối cùng, tham số lại phụ thuộc vào , do đó, ta phải xét mọi thỏa mãn để tính. Việc xét mọi từ đến sẽ khiến thuật toán quay về độ phức tạp . Do đó, ta cần dùng đến nhận xét rằng nếu:
Nói cách khác, ta chỉ cần xét từ đến vị trí đầu tiên thỏa , tức . Bây giờ, nếu cố định , ta có thể hình dung biến chạy trên các đoạn từ đến , tổng độ phức tạp tất cả các lần chạy là nên lúc này độ phức tạp trung bình của việc truy hồi đã trở thành .
Tổng kết lại, khi ta biết được giá trị của , ta thực hiện cập nhật các trạng thái khác của quy hoạch động như sau:
- Gán .
- Nếu , gán .
- Nếu , với mọi từ đến , gán .
Để biết đáp án cuối cùng của bài toán, ta kiểm tra . Như vậy, độ phức tạp của thuật toán này là . Bên cạnh đó, ta có thể giảm độ phức tạp bộ nhớ xuống nếu bỏ đi tham số trong bảng quy hoạch động.
¶ Cài đặt
Code tham khảo
// tìm điểm cắt
int breakPoint = 0, curSum = 0;
for (int i = 1; i <= n && curSum + w[i] <= C; i++)
curSum += w[i], breakPoint = i;
// chuẩn bị các tham số liên quan & trường hơp cơ sở
int W = *max_element(w + 1, w + 1 + n), offset = C - W;
for (int i = 0; i <= n; i++)
fill(change[i], change[i] + 2 * W + 1, INT_MAX);
change[0][curSum - offset] = 0;
// thực hiện QHĐ
for (int i = 0; i <= breakPoint; i++) {
for (int sigma = C - W; sigma <= C + W; sigma++) {
int cur = sigma - offset, delta = change[i][cur];
if (delta == INT_MAX) continue;
if (i < breakPoint) // bước 1
change[i + 1][cur] = min(change[i + 1][cur], delta);
if (sigma > C && i < breakPoint) // bước 2
change[i + 1][cur - w[i + 1]] = min(change[i + 1][cur - w[i + 1]], delta);
if (sigma <= C) { // bước 3
int dlt = min(n - breakPoint, (i ? change[i - 1][cur] : INT_MAX));
for (int j = delta + 1; j <= dlt; j++)
change[i][cur + w[breakPoint + j]] = min(change[i][cur + w[breakPoint + j]], j);
}
}
}
cout << (change[breakPoint][C - offset] < INT_MAX);
¶ Lời giải cho bài toán 0/1 Knapsack
Đặt , ta gọi làm hàm kiểm tra sự tồn tại của một trạng thái cân bằng có tổng trọng số , tổng giá trị khi thực hiện thao tác xóa/thêm món đồ trên lần lượt và phần tử đầu tiên của nhóm và .
Tương tự với lời giải trên, ta cũng định nghĩa dựa trên sự đồng biến của hàm trên biến . Như vậy, ta có lời giải .
Để cải tiến thêm cho thuật toán này, Pisinger đã đưa ra cận trên và cận dưới cho biến nhằm giới hạn số trạng thái cần duyệt. Tuy nhiên, cận trên cho độ phức tạp thời gian của thuật toán này vẫn là .
Nhìn chung, khi so sánh với các thuật toán quy hoạch động hiện tại, thuật toán của Pisinger chỉ phát huy hiệu quả với bài toán Subset Sum.
¶ Phụ lục
¶ Tài liệu tham khảo
- Ashley Khoo (errorgorn). [Tutorial] Knapsack, Subset Sum and the (max, +) Convolution, 2022.
- David Pisinger. Linear Time Algorithms for Knapsack Problems with Bounded Weights, 1997.
- Silvano Martello, David Pisinger, Paolo Toth. Dynamic Programming and Strong Bounds for the 0-1 Knapsack Problem, 1999.