¶ DP Sum over Subsets (DP SoS), phần 1
Người viết:
- Phạm Công Minh -- THPT Chuyên Khoa học Tự nhiên, Đại học Quốc gia Hà Nội.
- Nguyễn Tấn Minh -- THPT Chuyên Lê Hồng Phong, TPHCM.
Reviewer:
- Trần Xuân Bách -- University of Chicago.
- Nguyễn Minh Hiển -- Đại học Công nghệ, Đại học Quốc gia Hà Nội.
- Đoàn Gia Huy -- THPT Chuyên Khoa học Tự nhiên, Đại học Quốc gia Hà Nội.
- Nguyễn Quang Minh -- Michigan State University.
Trước khi bắt đầu, các bạn độc giả cần nắm được cách biểu diễn tập hợp nhỏ bằng bitmask và kỹ thuật Quy hoạch động bitmask cơ bản được trình bày ở bài viết này.
Trong bài viết này, các kí hiệu của phép toán trên tập hợp sẽ được áp dụng cho cả ngôn ngữ bitmask.
¶ Giới thiệu
Quy hoạch động Sum over Subsets (hay DP SoS) là một dạng nâng cao của Quy hoạch động bitmask cho phép chúng ta xử lý các bài toán liên quan đến việc tính tổng tập con của từng tập con cần xét một cách nhanh chóng. Không chỉ dừng lại ở việc tính tổng, DP SoS còn có thể được biến đổi linh hoạt để xử lý nhiều bài toán khác nhau.
¶ Bài toán kinh điển
Trước tiên, chúng ta hãy nghiên cứu cách sử dụng DP SoS để giải quyết bài toán sau: Xét các tập là tập con của , với mỗi tập như vậy, ta gán cho nó một giá trị . Ta cần tính giá trị hàm cho mọi tập con của tập theo công thức:
¶ Các lời giải vét cạn
Đối với phương pháp vét cạn, chúng ta có thể duyệt từng tập rồi từng tập và kiểm tra xem có phải tập con của hay không, cách làm này tốn độ phức tạp .
Ngoài ra, có thể tối ưu một chút bằng cách với mỗi tập , ta chỉ duyệt đúng các tập là tập con của với phương pháp duyệt tập con. Lúc này, mỗi bit trong bitmask có trạng thái: bit tắt ở tập cha, bit bật ở tập cha nhưng không được bật trong tập con, bit bật trong cả tập cha và tập con. Do đó, độ phức tạp thời gian là .
Code tham khảo
fill(f, f + (1 << n), a[0]); // do phương pháp duyệt tập con bỏ qua tập rỗng
for (int mask = 0; mask < (1 << n); mask++) {
for (int sub = mask; sub; sub = (sub - 1) & mask) f[mask] += a[sub];
}
¶ Ý tưởng & Thuật toán
Một bitmask là sub-mask của khi và chỉ khi (với là kí hiệu của phép bitwise AND). Đối với ngôn ngữ tập hợp, nếu bitmask biểu diễn một tập con của tập mà bitmask biểu diễn, thì là sub-mask của .
¶ Biểu diễn lại các trạng thái
¶ Ý tưởng chính
Ý tưởng dễ nghĩ đến nhất khi tiếp cận bài toán đó là đặt là tổng giá trị các sub-mask của mask (với là một bitmask biểu diễn tập hợp), rồi tìm cách tính từ các giá trị (với ). Tuy nhiên, cách này không mấy khả quan do các giá trị được truy hồi có thể trùng lắp nhau.
Xét mask , dễ thấy, các sub-mask của mask này là các mask chỉ có thể khác mask này tại bit thứ ---- những bit được bật của mask đang xét. Ta có thể gọi chung những mask như vậy bằng "pattern" .
Từ đó, ta có ý tưởng: Thay vì đặt trạng thái là một bitmask, ta có thể sử dụng pattern mà mỗi phần tử mang một trong ba giá trị , hoặc . Khi xét một pattern, các giá trị hoặc cho biết bit tương ứng của mask được cố định theo giá trị đó, còn dấu cho biết bit tương ứng mang trạng thái bật/tắt tùy ý.
Khi đó, là tổng giá trị các mask thỏa pattern . Ví dụ (các vị trí được tô màu đỏ là các vị trí không được cố định):
Để tính , ta tìm một dấu bất kì trong rồi truy hồi về hai trạng thái tương ứng được thay dấu đó bằng và . Ví dụ:
Lưu ý
Điểm mạnh của cách làm này là không có mask nào thỏa cả hai pattern và nên ta hoàn toàn có thể cộng hai giá trị mà không sợ bị tính trùng.
¶ Cải tiến ý tưởng
Tuy nhiên, cách làm này vẫn còn 2 điểm yếu lớn:
- Độ phức tạp của chúng ta vẫn là , thậm chí hằng số còn lớn hơn cách duyệt trâu.
- Việc biểu diễn các pattern dưới dạng biểu diễn tam phân rất rắc rối.
Để khắc phục điều này, khi truy hồi thay vì chọn dấu bất kì, ta quy ước chọn dấu bên trái nhất (chỉ số cao nhất). Khi đó, ta chỉ cần xét các pattern mà các giá trị và nằm ở hai bên của pattern.
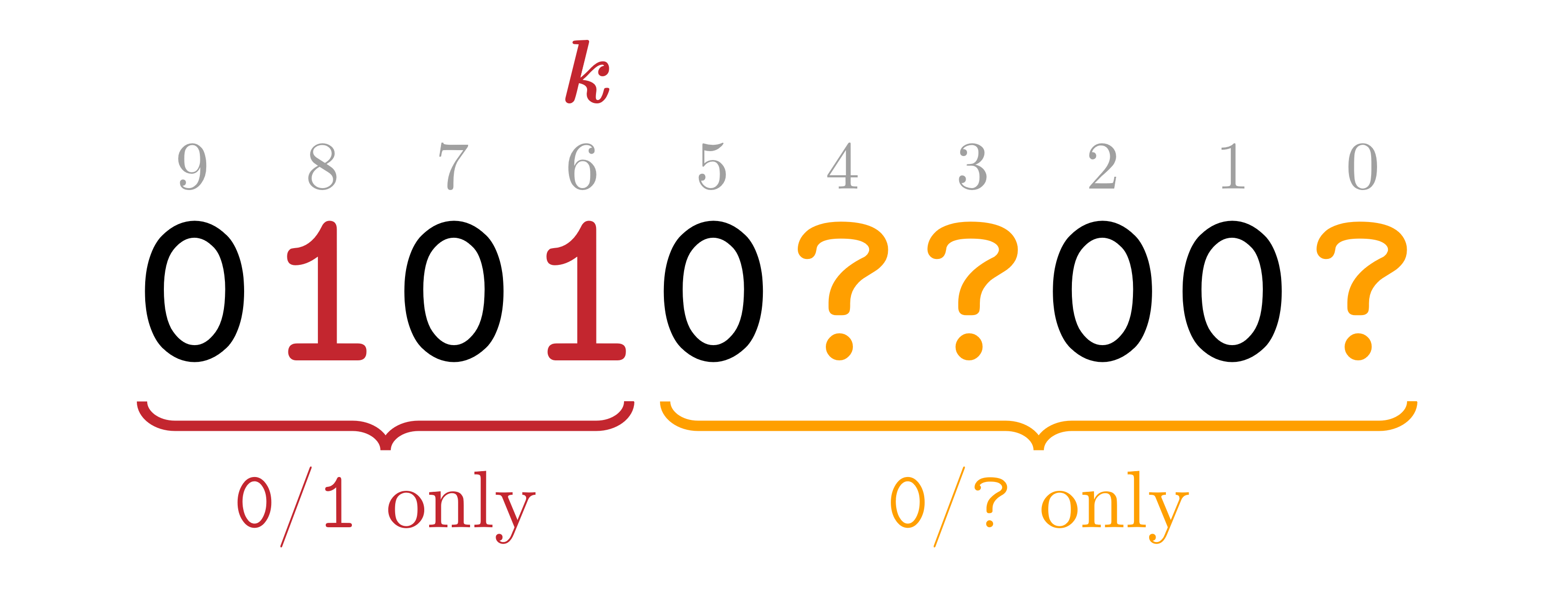
Ta lưu thêm một biến cho biết vị trí tách phần chứa và phần chứa (giá trị xuất hiện trong cả hai phần). Lúc này, để biểu diễn một pattern, ta chỉ cần một cặp bitmask và số nguyên :
- Các bit tắt của biểu diễn các giá trị của pattern.
- Các bit bật của trước vị trí biểu diễn các giá trị của pattern.
- Các bit bật của sau hoặc tại vị trí biểu diễn các giá trị của pattern.
Như vậy, ta đã giải quyết được cả vấn đề về độ phức tạp và việc biểu diễn các pattern.
¶ Xây dựng hàm Quy hoạch động
Bây giờ, hàm Quy hoạch động của chúng ta là tính tổng giá trị của các mask thỏa pattern theo cách đặt trạng thái như trên. Trường hợp cơ sở là (pattern không có dấu ).
Với mỗi trạng thái , ta tìm dấu bên trái nhất để truy hồi. Cụ thể:
- Nếu giá trị thứ trong pattern là , tức bit thứ của bật, đây sẽ là dấu cần tìm nên ta thực hiện truy hồi theo công thức:
- Nếu giá trị thứ trong pattern là , tức bit thứ của tắt, ta sẽ tìm tiếp dấu ở trạng thái :
Cuối cùng, ta có (pattern chỉ có dấu và giá trị ).
Như vậy, ta có công thứ truy hồi hoàn chỉnh là:
Sau đây là cây biểu diễn các trạng thái mà ta sẽ gọi khi tính :
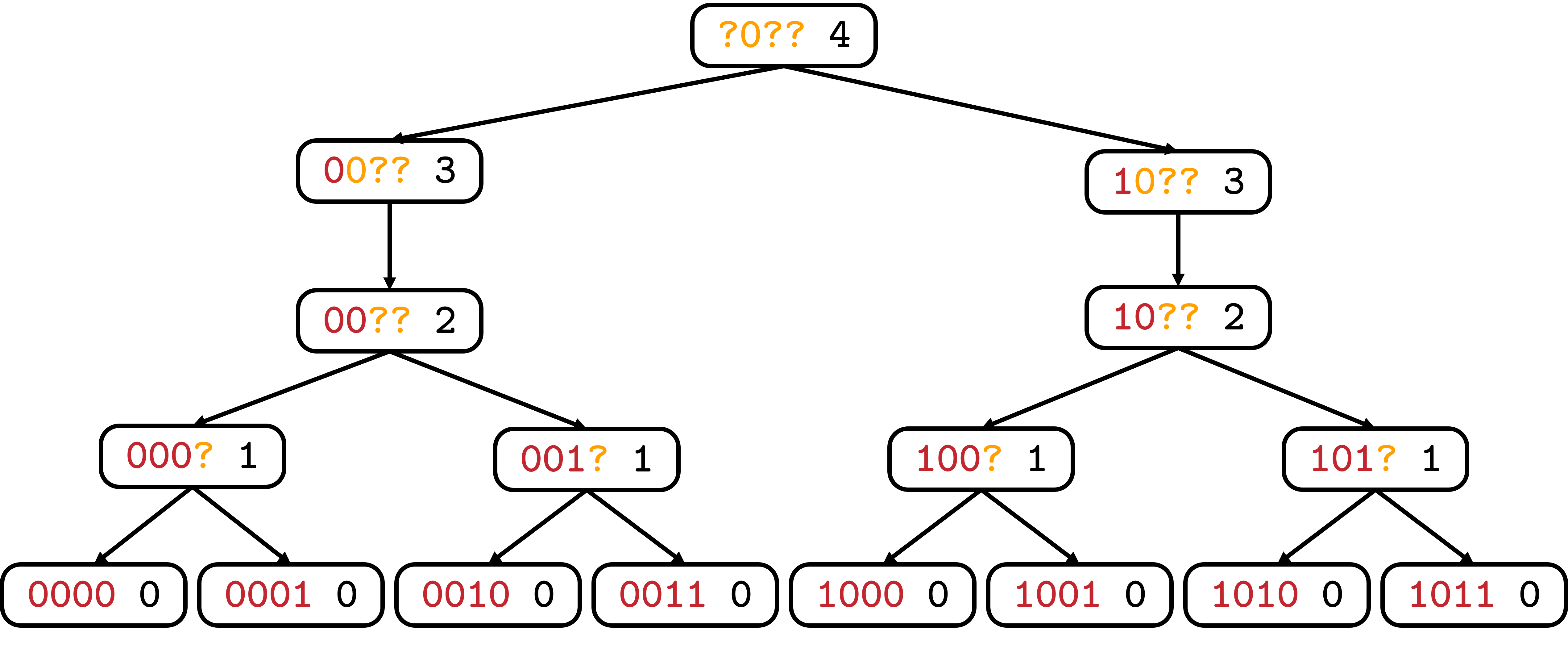
Lưu ý, khi vẽ hết các trạng thái của Quy hoạch động ra, đồ thị không còn là cây nữa mà là một đồ thị có hướng không chu trình (DAG).
Có tổng cộng là trạng thái Quy hoạch động, mỗi trạng thái được truy hồi trong . Như vậy, ta đã có thuật toán Quy hoạch động Sum over Subsets có độ phức tạp:
- Thời gian: .
- Bộ nhớ: hoặc tùy cách cài đặt.
¶ Cài đặt
Với công thức truy hồi như trên, khi cài đặt, việc duyệt theo biến hay trước đều đúng. Tuy nhiên, mỗi cách làm có ưu/nhược điểm riêng nên ta sẽ tìm hiểu cả hai.
¶ Cách 1
Ta sẽ duyệt theo biến trước:
for (int mask = 0; mask < (1 << n); mask++) {
dp[mask][0] = a[mask]; // trường hợp cơ sở
for (int k = 1; k <= n; k++) {
if (mask & (1 << (k - 1)))
dp[mask][k] = dp[mask ^ (1 << (k - 1))][k - 1] + dp[mask][k - 1];
else dp[mask][k] = dp[mask][k - 1];
}
f[mask] = dp[mask][n];
}
Ưu điểm của cách cài đặt này là khi bắt đầu tính cho một bất kì, ta đã có kết quả của mọi trạng thái liên quan đến sub-masks của , do đó, cách này còn được gọi là "online" DP SoS. Điều này vô cùng hữu ích đối với những bài DP SoS có công thức tự gọi lại chính nó.
Tuy nhiên, cách làm này không thể tối ưu bộ nhớ xuống được.
¶ Cách 2
Ta sẽ duyệt theo biến trước:
for (int mask = 0; mask < (1 << n); mask++) dp[mask][0] = a[mask]; // trường hợp cơ sở
for (int k = 1; k <= n; k++) {
for (int mask = 0; mask < (1 << n); mask++) {
if (mask & (1 << (k - 1)))
dp[mask][k] = dp[mask ^ (1 << (k - 1))][k - 1] + dp[mask][k - 1];
else dp[mask][k] = dp[mask][k - 1];
}
}
for (int mask = 0; mask < (1 << n); mask++) f[mask] = dp[mask][n];
Với cách này, tất cả các giá trị sẽ được đồng loạt tính xong ở vòng cuối (khi ). Do đó, giả sử trong quá trình tính , ta cần biết thì cách làm này không phù hợp.
Bù lại, từ cách cài đặt này, ta có thể tối ưu bộ nhớ xuống và rút gọn được phần cài đặt xuống rất ngắn. Do đó, nhìn chung, cách làm này phổ biến hơn cách 1.
¶ Tối ưu bộ nhớ
Ở cách 2, có thể thấy rằng khi duyệt đến , ta chỉ cần duy trì các giá trị . Từ đó, ta có thể đưa biến lên trước trong cách đặt trạng thái và chỉ duy trì dòng của bảng Quy hoạch động, hay thậm chí là dòng nếu ta duyệt các mask từ lớn đến nhỏ (ý tưởng tương tự DP Knapsack).
for (int k = 1; k <= n; k++)
for (int mask = (1 << n) - 1; mask >= 0; mask--)
if (mask & (1 << (k - 1))) dp[mask] += dp[mask ^ (1 << (k - 1))];
Để cài đặt ngắn gọn hơn nữa, ta còn có thể đưa ra nhận xét rằng đối với DP SoS, việc duyệt các mask từ nhỏ đến lớn cũng không làm sai kết quả. Hơn nữa, vì không còn cần phải đánh số dòng trên bảng QHĐ, ta có thể duyệt từ đến và coi trường hợp cơ sở là , sẽ thuật tiện hơn cho việc xử lý bitmask. Đến đây, ta đã có code DP SoS rất ngắn, dễ cài đặt, tối ưu bộ nhớ và hằng số thấp:
for (int k = 0; k < n; k++)
for (int mask = 0; mask < (1 << n); mask++)
if (mask & (1 << k)) dp[mask] += dp[mask ^ (1 << k)];
Tại sao có thể duyệt các mask từ nhỏ đến lớn?
Khi duyệt các mask từ nhỏ đến lớn, ta sẽ vô tình truy hồi về giá trị đã được cập nhật sang dòng mới, từ đó, công thức Quy hoạch động của chúng ta sẽ bị "sai" đi một chút:
Điểm khác biệt là ở trường hợp thứ hai, ta truy hồi về thay vì . Tuy nhiên, để ý rằng vì nên theo công thức truy hồi:
¶ Các biến thể của DP SoS
¶ Bài toán ngược
Cho trước các giá trị của hàm . Khôi phục mảng ban đầu, nói cách khác, tìm mảng gồm phần tử sao cho .
¶ Công thức truy hồi
Bằng cách đổi vế công thức truy hồi của DP SoS, ta có công thức truy hồi để xử lý bài toán ngược như sau:
Đáp án bây giờ là .
Code tham khảo
for (int mask = 0; mask < (1 << n); mask++) {
for (int k = n - 1; k >= 0; k--) {
if (mask & (1 << k))
dp[mask][k] = dp[mask][k + 1] - dp[mask ^ (1 << k)][k];
else dp[mask][k] = dp[mask][k + 1];
}
}
¶ Tối ưu bộ nhớ
Tương tự bài toán gốc, ta cũng có thể tối ưu bộ nhớ.
Code tham khảo
for (int k = n - 1; k >= 0; k--)
for (int mask = 0; mask < (1 << n); mask++)
if (mask & (1 << k)) sos[mask] -= sos[mask ^ (1 << k)];
¶ Bao hàm loại trừ: Mobius Transform
¶ Bài toán kinh điển
Cho đối tượng , giả sử rằng với mọi tập con của đối tượng này, ta có thể tính kích thước của giao của các đối tượng thuộc tập con, gọi là . Sử dụng bao hàm loại trừ, ta có thể tính kích thước của hợp của đối tượng này bằng công thức:
Giả sử với mọi tập con của đối tượng này, ta cần tính kích thước của hợp của các đối tượng thuộc tập con, gọi là . Một lần nữa, áp dụng bao hàm loại trừ, ta có:
Ta có thể áp dụng DP SoS để tính mọi giá trị trong .
Code tham khảo
for (int mask = 0; mask < (1 << n); mask++)
sos[mask] = intersect[mask] * (__builtin_parity(mask) ? 1 : -1);
for (int k = 0; k < n; k++)
for (int mask = 0; mask < (1 << n); mask++)
if (mask & (1 << k)) sos[mask] += sos[mask ^ (1 << k)];
Ở cuối chương trình, mảng sos chứa các giá trị của mảng .
¶ Biển thể
Ngoài ra, ta có thể sử dụng bao hàm loại trừ để xử lý bài toán DP SoS ngược nêu trên. Trước tiên, khi xét bit:
Với bit, ta có:
Sử dụng Bao hàm loại trừ, ta có công thức tổng quát:
Chứng minh
Để chứng minh công thức trên, ta tính đóng góp của từng giá trị của sub-mask (với ) vào tổng.
Với , ta thấy đóng góp đúng một lần vào tổng vì được tính trong . Hơn nữa, nên dấu của luôn là dương.
Với , ta thấy đóng góp của sẽ phụ thuộc vào các thỏa , hay . Cụ thể, đóng góp của vào tổng là:
Do ta chỉ quan tâm kích thước của nên ta đặt và biến đổi công thức thành:
Đem nhân tử chung ra ngoài và đặt phần còn lại là , ta sử dụng Nhị thức Newtown để biến đổi:
Như vậy, đóng góp của mọi giá trị với là .
Đến đây, ta còn phải biến đổi công thức một chút để có thể áp dụng Mobius Transform, cụ thể như sau:
Sau khi biến đổi, từng số hạng trong tổng đã độc lập theo , do đó, ta có thể áp dụng DP SoS để tính nhanh rồi nhân thêm để được trong .
Code tham khảo
for (int mask = 0; mask < (1 << n); mask++)
sos[mask] = f[mask] * (__builtin_parity(mask) ? -1 : 1);
for (int k = 0; k < n; k++)
for (int mask = 0; mask < (1 << n); mask++)
if (mask & (1 << k)) sos[mask] += sos[mask ^ (1 << k)];
for (int mask = 0; mask < (1 << n); mask++)
a[mask] = sos[mask] * (__builtin_parity(mask) ? -1 : 1);
¶ Sum over Proper Subsets
Xét bài toán kinh điển của DP SoS, nhưng công thức đổi lại thành:
tức là ta không xét là tập con của chính nó nữa.
Thông thường, ta có thể giải bài toán Sum over Subsets như bình thường, sau đó trừ đi . Tuy nhiên, đối với một số bài toán, ta cần phải tính toán khi chưa biết . Khi đó, ta cần xây dựng một công thức Quy hoạch động không dùng đến .
Để làm được điều đó, ta thêm ràng buộc pattern không tính mask được tạo thành bằng cách thay mọi dấu của nó thành bit bật. Lúc này, công thức truy hồi sẽ được chỉnh sửa thành:
với .
¶ Sum over subsets, truy hồi chính nó
Nâng cấp bài toán kinh điển của DP SoS thêm một chút, lúc này, hàm sẽ tự truy hồi chính nó:
với là một hàm ánh xạ bất kì.
Ý tưởng chính để giải quyết dạng bài này là ta sẽ duy trì song song giá trị của và . Lúc này, ta quay trở lại với cách cài đặt thứ nhất của DP SoS kết hợp với biến thể Sum over Proper Subsets được trình bày ở trên. Điều này giúp ta có thể biết trước mọi giá trị trước khi bắt đầu tính (với ).
Code tham khảo
for (int mask = 0; mask < (1 << n); mask++) {
dp[mask][0] = 0; // trường hợp cơ sở
for (int k = 1; k <= n; k++) {
// tính dp
if (mask & (1 << (k - 1))) {
int sub = mask ^ (1 << (k - 1));
dp[mask][k] = dp[mask][k - 1] + dp[sub][k - 1] + f[sub];
}
else dp[mask][k] = dp[mask][k - 1];
}
f[mask] = h(dp[mask][n]) + a[mask]; // tính f
}
¶ Sum over subsets, hai hàm gọi chéo nhau
Nâng cấp bài tập ở trên thêm một chút nữa, ta cần tính hai hàm có định nghĩa như sau:
với hàm là hai hàm ánh xạ tương tự bài toán ở trên.
Lúc này, ta sẽ duy trì đồng thời giá trị:
- Hai hàm .
- Quy hoạch động trên hàm là (theo kiểu sum over subset).
- Quy hoạch động trên hàm là (theo kiểu sum over proper subset).
Để tính các giá trị này, ta kết hợp các ý tưởng đã sử dụng ở các phần trên.
Code tham khảo
for (int mask = 0; mask < (1 << n); mask++) {
// tính dpG và f
for (int k = 1; k <= n; k++) {
if (mask & (1 << (k - 1))) { // truy hồi theo kiểu proper subset
int sub = mask ^ (1 << (k - 1));
dpG[mask][k] = dpG[mask][k - 1] + dpG[sub][k - 1] + g[sub];
}
else dpG[mask][k] = dpG[mask][k - 1];
}
f[mask] = h1(dpG[mask][n]) + a[mask];
// tính dpF và g
dpF[mask][0] = f[mask];
for (int k = 1; k <= n; k++) {
if (mask & (1 << (k - 1))) // truy hồi theo kiểu subset
dpF[mask][k] = dpF[mask][k - 1] + dpF[mask ^ (1 << (k - 1))][k - 1];
else dpF[mask][k] = dpF[mask][k - 1];
}
g[mask] = h2(dpF[mask][n]) + b[mask];
}
¶ Bài tập ứng dụng
Bạn đọc nên tự thử sức trước với các bài tập dưới đây trước khi bước vào phần phân tích ý tưởng và cài đặt nhé.
Trong phần này, ta quy ước , và lần lượt là ký hiệu của phép bitwise OR, bitwise AND và bitwise XOR.
¶ CSES - Bit Problem
Cho một danh sách số nguyên, với mọi số trong danh sách, gọi là , hãy tính:
- Số phần tử thuộc danh sách sao cho .
- Số phần tử thuộc danh sách sao cho .
- Số phần tử thuộc danh sách sao cho .
¶ Giới hạn
- .
- .
¶ Ý tưởng
Nếu biến đổi thành ngôn ngữ bitmask thuần túy, các yêu cầu lần lượt là: đếm số mask là sub-mask của ; đếm số mask là super-mask của ; và đếm số mask có ít nhất một bit bật chung với .
Đối với yêu cầu 1, ta dựng mảng thống kê rồi thực hiện DP SoS căn bản trên mảng thống kê này. Tương tự với yêu cầu loại 2, ta cũng thực hiện DP SoS với định nghĩa DP thay đổi một chút: các bit bật của biểu diễn giá trị của pattern, các bit tắt biểu diễn giá trị hoặc tùy theo . Việc xây dựng công thức truy hồi cũng được thực hiện tương tự.
Đối với yêu cầu cuối cùng, ta sẽ đếm số mask không có bit bật chung với rồi thực hiện bù trừ. Phân tích một chút, khi xét một bitmask , để không có bit bật chung với thì:
- Nếu bit thứ của được bật, bit tương ứng của bắt buộc phải tắt.
- Ngược lại, bit tương ứng của là gì cũng được.
Đến đây, ta có thể thấy rằng là sub-mask của sau khi đã lật hết tất cả các bit của .
Nói tóm lại, chúng ta cần tính hai giá trị sau:
- là số phần tử trong dãy là sub-mask của .
- là số phần tử trong dãy là super-mask của .
¶ Độ phức tạp
- Độ phức tạp thời gian: với .
- Độ phức tạp bộ nhớ: .
¶ Cài đặt
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
const int full = (1 << 20) - 1;
int a[1 << 20], sosSub[1 << 20], sosSup[1 << 20];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n; cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
sosSub[a[i]]++, sosSup[a[i]]++;
}
for (int k = 0; k < 20; k++) {
for (int mask = 0; mask < (1 << 20); mask++) {
if (mask & (1 << k)) sosSub[mask] += sosSub[mask ^ (1 << k)];
else sosSup[mask] += sosSup[mask ^ (1 << k)];
}
}
for (int i = 0; i < n; i++)
cout << sosSub[a[i]] << " " << sosSup[a[i]] << " " << n - sosSub[a[i] ^ full] << "\n";
return 0;
}
¶ Codeforces 1208F - Bits and Pieces
Cho dãy gồm phần tử, hãy tính:
¶ Giới hạn
- .
- .
¶ Ý tưởng
Nhận xét quan trọng ta cần đưa ra ở bài toán này là: Nếu tồn tại một phương án là super-mask của thì cũng tồn tại một phương án là super-mask của (với ). Đến đây, ta sẽ nghĩ đến thuật toán tìm kiếm nhị phân trên bit.
Bên cạnh việc sử dụng trong các bài toán tìm kiếm nhị phân truyền thống để đạt hằng số thấp, thuật toán tìm kiếm nhị phân trên bit còn có thể giải quyết bài toán tìm lớn nhất sao cho với là khoảng tìm kiếm và là một hàm thỏa:
- Với mọi , ta có .
- Nếu thì với .
Thuật toán này dựa trên ý tưởng tham lam tương tự thuật toán Walk on Trie đó là thử bật các bit của đáp án theo thứ tự từ lớn đến bé. Ta có thể đưa ra nhận xét là việc bật bit thứ và tắt các bit từ đến vẫn cho ra kết quả lớn hơn việc tắt bit thứ và bật tất cả các bit từ đến . Nói cách khác:
Nhìn chung, các thuật toán tìm kiếm nhị phân trên bit có mô hình cài đặt như sau:
int ans = 0;
for (int mask = (1 << B); mask; mask >>= 1) {
if (f(ans | mask)) ans |= mask;
}
Nhiệm vụ còn lại là thiết kế một hàm để kiểm tra xem liệu có tồn tại một phương án là super-mask của . Để làm điều này, ta cố định trước giá trị và tìm những bit chưa được bật ở nhưng lại được bật ở (những bit còn thiếu), gọi là bitmask . Sau đó, ta tìm một cặp sao cho và là super-mask của .
Dễ thấy, điều kiện duy nhất để là cả và phải là super-mask của . Từ đây, ta có thể tham lam chọn hai chỉ số là lớn nhất và lớn nhì sao cho và đều là super-mask của . Ta có thể sử dùng DP SoS để tính trước là hai chỉ số lớn nhất sao cho phần tử tương ứng là super-mask của , sau đó tìm trong . Lưu ý, nếu thì ta coi như không tìm được cặp thỏa mãn.
¶ Độ phức tạp
- Độ phức tạp thời gian: với .
- Độ phức tạp bộ nhớ: .
¶ Cài đặt
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
struct helper {
int best, secBest;
helper() : best(0), secBest(0) {}
void push (int cur) {
if (cur > best) secBest = best, best = cur;
else secBest = max(secBest, cur);
}
void push (const helper &o) {
if (best >= o.best) secBest = max(secBest, o.best);
else secBest = max(best, o.secBest), best = o.best;
}
} sos[1 << 21];
int a[1 << 20], n;
bool ok (int mask) {
for (int i = 1; i <= n - 2; i++) {
int miss = mask ^ (mask & a[i]);
if (i < sos[miss].secBest) return 1;
}
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
sos[a[i]].push(i);
}
for (int k = 0; k < 21; k++)
for (int mask = 0; mask < (1 << 21); mask++)
if (!(mask & (1 << k))) sos[mask].push(sos[mask ^ (1 << k)]);
int ans = 0;
for (int mask = 1 << 20; mask > 0; mask >>= 1)
if (ok(ans | mask)) ans |= mask;
cout << ans;
return 0;
}
¶ VOI 2021 - Phép toán OR
Cho dãy gồm phần tử và ba số nguyên . Đếm số dãy con (không nhất thiết phải liên tiếp) độ dài của thỏa mãn:
- Gọi là bitwise OR của các số trong dãy con thì và .
In ra đáp án modulo .
¶ Giới hạn
- .
- .
¶ Ý tưởng
Thực chất thì để giải bài toán này, ta chỉ cần tính là số dãy con độ dài sao cho bitwise OR của chúng là . Sau đó, ta duyệt mọi bội của trong khoảng và tính tổng.
Ta định nghĩa là số dãy con độ dài sao cho bitwise OR của chúng là một sub-mask của . Giá trị mảng dễ tính hơn nhiều và ta cũng có thể khôi phục mảng từ sử dụng DP SoS ngược hoặc bao hàm loại trừ.
Dễ thấy, để bitwise OR của một dãy là một sub-mask của thì mọi phần tử của dãy phải là sub-mask của . Như vậy, gọi là số phần tử là sub-mask của , ta có thể dùng tổ hợp để tính :
Cuối cùng, ta thực hiện DP SoS ngược trên mảng là đã có mảng trong .
¶ Độ phức tạp
- Độ phức tạp thời gian: với .
- Độ phức tạp bộ nhớ: .
¶ Cài đặt
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
const int mn = 1e6 + 6;
int fact[mn], ifac[mn], sos[1 << 20];
int add (int a, int b) { return a + b - (a + b < MOD ? 0 : MOD); }
int sub (int a, int b) { return a - b + (a - b >= 0 ? 0 : MOD); }
int mul (int a, int b) { return 1LL * a * b % MOD; }
int binpow (int a, int b = MOD - 2) {
int ans = 1;
for (; b; b >>= 1) {
if (b & 1) ans = mul(ans, a);
a = mul(a, a);
}
return ans;
}
int C (int n, int k) {
if (n < k) return 0;
int ans = mul(fact[n], ifac[k]);
return mul(ans, ifac[n - k]);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
// tiền xử lý của tổ hợp
fact[0] = 1;
for (int i = 1; i < mn; i++) fact[i] = mul(fact[i - 1], i);
ifac[mn - 1] = binpow(fact[mn - 1]);
for (int i = mn - 2; i >= 0; i--) ifac[i] = mul(ifac[i + 1], i + 1);
// nhập dữ liệu
int n, k, L, R; cin >> n >> k >> L >> R;
for (int i = 0; i < n; i++) {
int a; cin >> a;
sos[a]++;
}
// tính f bằng DP SoS truyền thống
for (int k = 0; k < 20; k++)
for (int mask = 0; mask < (1 << 20); mask++)
if (mask & (1 << k)) sos[mask] += sos[mask ^ (1 << k)];
// tính sub bằng tổ hợp
for (int mask = 0; mask < (1 << 20); mask++) sos[mask] = C(sos[mask], k);
// tính count bằng DP SoS ngược
for (int k = 19; k >= 0; k--)
for (int mask = 0; mask < (1 << 20); mask++)
if (mask & (1 << k)) sos[mask] = sub(sos[mask], sos[mask ^ (1 << k)]);
// lấy đáp án
int ans = 0;
for (int mask = 3 * (L / 3 + (L % 3 ? 1 : 0)); mask <= R; mask += 3) ans = add(ans, sos[mask]);
cout << ans;
return 0;
}
¶ JOI 2018 - Snake Escaping
Cho dãy gồm số nguyên tương ứng giá trị của tập con của và truy vấn. Với mỗi truy vấn, cho xâu độ dài là pattern gồm một trong ba ký tự , tính tổng giá trị tương ứng của các tập thỏa pattern được cho.
¶ Giới hạn
- .
- .
- .
¶ Ý tưởng
Một trong những nhận xét quan trọng nhất mà ta cần đưa ra để xử lý bài toán này là: tần suất xuất hiện của ký tự xuất hiện ít nhất là không quá . Tức là với lần lượt là tần suất xuất hiện của từng loại ký tự trong xâu.
Chứng minh
Ta có thể sử dụng phản chứng: Giả sử tồn tại một pattern mà mọi ký tự đều xuất hiện ít nhất lần. Khi đó, tổng số ký tự tối thiểu của pattern sẽ là , không đúng với giới hạn đề bài.
Đây là giới hạn đủ nhỏ để duyệt sub-mask. Từ đó, ta có ý tưởng trả lời truy vấn bằng cách duyệt sub-mask trên ký tự xuất hiện ít nhất trong .
¶ Trường hợp 1: Ký tự xuất hiện ít nhất
Đây là trường hợp dễ xử lý nhất, ta đơn giản là duyệt tất cả các bitmask thỏa pattern và tính tổng tương ứng là xong. Độ phức tạp của trường hợp này là .
¶ Trường hợp 2: Ký tự xuất hiện ít nhất
Gọi lần lượt là tập các vị trí xuất hiện của ký tự và . Để đảm bảo độ phức tạp, ta chỉ có thể duyệt tập con của .
Gọi là tổng giá trị các mask thỏa (với ), có thể được tính bằng DP SoS. Từ hàm , ta có thể tính đáp án bằng Bao hàm loại trừ như sau:
Như vậy, ta giải quyết được trường hợp này trong .
¶ Trường hợp 3: Ký tự xuất hiện ít nhất
Đối với trường hợp này, ta lại sử dụng Bao hàm loại trừ tương tự trường hợp 2. Gọi lần lượt là tập các vị trí xuất hiện của ký tự và , là tổng giá trị các mask thỏa (với ). Hàm cũng có thể được tính bằng DP SoS.
Độ phức tạp của trường hợp cuối cùng là .
¶ Độ phức tạp
- Độ phức tạp thời gian: .
- Độ phức tạp bộ nhớ: .
¶ Cài đặt
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
int toxic[1 << 20], sosSub[1 << 20], sosSuper[1 << 20];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int k, Q; cin >> k >> Q;
for (int i = 0; i < (1 << k); i++) {
char c; cin >> c;
toxic[i] = sosSub[i] = sosSuper[i] = c - '0';
}
for (int i = 0; i < k; i++) {
for (int mask = 0; mask < (1 << k); mask++) {
if (mask & (1 << i)) sosSub[mask] += sosSub[mask ^ (1 << i)];
else sosSuper[mask] += sosSuper[mask ^ (1 << i)];
}
}
int full = (1 << k) - 1;
while (Q--) {
string s; cin >> s;
reverse(s.begin(), s.end());
int maskZ = 0, maskO = 0, maskQ = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '0') maskZ |= (1 << i);
if (s[i] == '1') maskO |= (1 << i);
if (s[i] == '?') maskQ |= (1 << i);
}
int ans = 0;
if (__builtin_popcount(maskQ) <= 6) {
ans = toxic[maskO];
for (int sub = maskQ; sub; sub = (sub - 1) & maskQ)
ans += toxic[sub | maskO];
}
else if (__builtin_popcount(maskO) <= 6) {
ans = sosSub[maskQ] * (__builtin_parity(maskO) ? -1 : 1);
for (int sub = maskO; sub; sub = (sub - 1) & maskO) {
if (__builtin_parity(sub) ^ __builtin_parity(maskO)) ans -= sosSub[sub | maskQ];
else ans += sosSub[sub | maskQ];
}
}
else if (__builtin_popcount(maskZ) <= 6) {
ans = sosSuper[maskO];
for (int sub = maskZ; sub; sub = (sub - 1) & maskZ) {
if (__builtin_parity(sub)) ans -= sosSuper[sub | maskO];
else ans += sosSuper[sub | maskO];
}
}
cout << ans << "\n";
}
return 0;
}
¶ Phụ lục
¶ Luyện tập thêm
- Codeforces 1185F - Two Pizzas
- Codeforces 1043F - Make It One
- Codeforces 986C - AND Graph
- Codechef - Strange Functions
- AtCoder 137D - Prefix XORs
- Kilonova - XorTransform
- Codeforces 1620G - Subsequences Galore
- Codeforces 1326F2 - Wise Men
- Codeforces 1713F - Lost Array
- AtCoder 136D - Without Carry
Ngoài ra, bạn đọc có thể tìm kiếm thêm những bài tập khác để trau dồi kỹ năng xử lý những dạng toán liên quan tại đây.