¶ Hình học tính toán phần 3: Đa giác
Tác giả:
- Nguyễn Đức Kiên - Trường Đại học Công nghệ, ĐHQGHN
Reviewers:
- Nguyễn Tấn Minh – THPT Chuyên Lê Hồng Phong, TPHCM
- Võ Đức Đoàn - THPT Chuyên Nguyễn Tất Thành - Kon Tum
- Nguyễn Minh Hiển – Trường Đại học Công nghệ, ĐHQGHN
Tiếp nối hai phần trước của series Hình học tính toán, trong bài viết này, ta sẽ tập trung vào các bài toán liên quan đến đa giác, diện tích đa giác và tính chất của các điểm thuộc đa giác.
Các bài viết trước thuộc series Hình học tính toán:
¶ Kiến thức cơ bản về đa giác
¶ Một số thuật ngữ
Phần dưới đây liệt kê một số thuật ngữ quen thuộc với đa giác:
- Đa giác (polygon) là một đường gấp khúc khép kín. Nghĩa là, nó là một tập hợp các đoạn thẳng, sao cho hai đoạn thẳng liên tiếp nhau (đoạn cuối cùng và đoạn đầu tiên cũng tính là hai đoạn liên tiếp) cắt nhau tại một đầu mút của hai đoạn thẳng đó.
- Cạnh (edge hoặc side) của đa giác là các đoạn thẳng tạo nên đa giác
- Đỉnh (vertex, số nhiều vertices) của đa giác là các đầu mút của các đoạn thẳng tạo nên đa giác. Hiển nhiên, đa giác có đỉnh thì sẽ có cạnh và ngược lại. Do vậy, người ta thường nhóm các loại đa giác lại theo số cạnh (cũng là số đỉnh) và gọi nó bằng những cái tên quen thuộc như tam giác (triangle), tứ giác (quadrilateral), ngũ giác (pentagon), lục giác (hexagon), ... cho đến hình -cạnh (-gon). Các đa giác được gọi tên bằng các đỉnh theo thứ tự cùng hoặc ngược chiều kim đồng hồ, chẳng hạn dưới đây ta có hình 7 cạnh :

- Đa giác lồi (convex polygon) là loại đa giác mà trong đó với hai đỉnh bất kỳ thuộc đa giác, đoạn thẳng nối hai đỉnh đó nằm hoàn toàn trong đa giác. Nói cách khác, nếu kéo dài tất cả các cạnh của đa giác ra thì chúng sẽ không cắt nhau ở vị trí nào nằm bên trong đa giác. trong hình trên là một đa giác lồi.
- Đường chéo (diagonal) của một đa giác là đoạn thẳng nối hai đỉnh không kề nhau của đa giác. Với đa giác trên, nếu nối và lại ta có một đường chéo
- Đa giác đều (regular polygon) là đa giác có tất cả các cạnh và các góc giữa hai cạnh kề nhau là bằng nhau.
Lưu ý: Trong bài viết này, nếu không có chú thích gì thêm, khi nhắc đến "đa giác" chúng ta sẽ hiểu đó là đa giác lồi.
¶ Một số tính chất của đa giác
- Tổng các góc trong đa giác cạnh là độ.
- Trong đa giác lồi cạnh, tại mỗi đỉnh ta vẽ được đường chéo, cùng với các cạnh chúng tạo ra tam giác con. Như vậy, từ các đỉnh trong đa giác, ta có thể vẽ được nhiều nhất đường chéo.
- Các đa giác đều có chẵn cạnh vừa có tâm đối xứng vừa có trục đối xứng, còn các đa giác đều có lẻ cạnh thì chỉ có tâm đối xứng.
- Bất đẳng thức đa giác: Độ dài một cạnh bất kỳ của một đa giác lồi luôn nhỏ hơn tổng độ dài các cạnh còn lại. Cụ thể, trong đa giác gồm cạnh có độ dài lần lượt là , , ..., , ta có:
Bất đẳng thức cũng có thể được biểu diễn sử dụng cạnh lớn nhất trong đa giác:
¶ CTDL biểu diễn
Để có thể giải quyết các bài toán hình học tính toán một cách hiệu quả, ta nên xây dựng các struct riêng cho từng đối tượng.
Trong bài này, các điểm, vector và đa giác sẽ được cài đặt bằng các CTDL sau:
#include <vector>
using namespace std;
struct Point{
int x;
int y;
// Khởi tạo mặc định
Point();
// Khởi tạo điểm từ toạ độ
Point(int __x, int __y): x(__x), y(__y) {}
};
struct Vector {
int x;
int y;
// Khởi tạo mặc định vector
Vector();
// Khởi tạo vector từ điểm đầu và điểm cuối
Vector(Point p, Point q): x(q.x - p.x), y(q.y - p.y) {}
// Tích có hướng của vector hiện tại và một vector khác
long long operator ^ (const Vector &v2) const {
return 1ll * x * v2.y - 1ll * y * v2.x;
}
};
struct Polygon {
// Số đỉnh thuộc đa giác
int nVertices;
// Danh sách các đỉnh thuộc đa giác
vector <Point> vertices;
// Khởi tạo mặc định
Polygon();
// Khởi tạo tam giác từ các đỉnh
Polygon(Point A, Point B, Point C) : vertices({A, B, C}), nVertices(3) {}
// Khởi tạo đa giác từ danh sách đỉnh
Polygon(const vector <Point> &__vertices) : vertices(__vertices), nVertices(__vertices.size()) {}
// Diện tích, được cài đặt tại phần Diện tích đa giác
double area();
// Hai lần diện tích, được cài đặt tại phần Diện tích đa giác
long long area2();
};
¶ Diện tích đa giác
Độ lớn của phần mặt phẳng bị chiếm chỗ bởi một đa giác được gọi là diện tích của đa giác đó. Người ta thường dùng chữ để ký hiệu diện tích, chẳng hạn diện tích ngũ giác có thể được ký hiệu là .
Bài toán: VNOJ - Diện tích đa giác
Tóm tắt đề bài: Cho đa giác lồi được tạo thành từ điểm cho trước theo đúng thứ tự đó, điểm thứ trong số đó có toạ độ là . Tính diện tích đa giác trên.
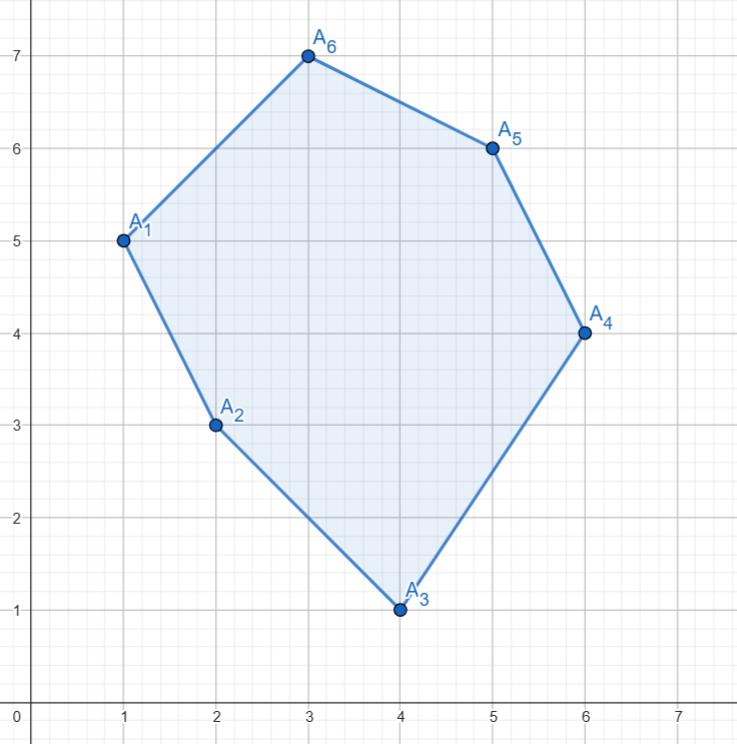
¶ Ý tưởng
Gọi điểm thuộc đa giác theo đúng thứ tự trên là , trong đó là điểm có tung độ nhỏ nhất trong số các điểm cùng có hoành độ nhỏ nhất. Để tiện biểu diễn các công thức, trong bài viết này ta sẽ quy ước thêm .
Các công thức tính diện tích cho tam giác và một số dạng tứ giác đặc biệt vốn đã rất phổ biến. Tuy vậy, gần như chẳng có công thức nào cho phép ta tính ngay diện tích của một đa giác bất kỳ (ngay cả tứ giác đã khó rồi). Chỉ có một cách duy nhất để giải bài toán này: chia hình này thành những hình có thể tính được diện tích.
¶ Công thức Shoelace (công thức tam giác)
Nếu bài toán trên xuất hiện trong đề thi vào THPT, với một hình vẽ chẳng có tính chất gì đặc biệt cả, ta đành phải chọn cách chia đơn giản nhất: đường chéo. Tại một đỉnh của đa giác, vẽ các đường chéo đến tất cả các đỉnh không kề với nó:
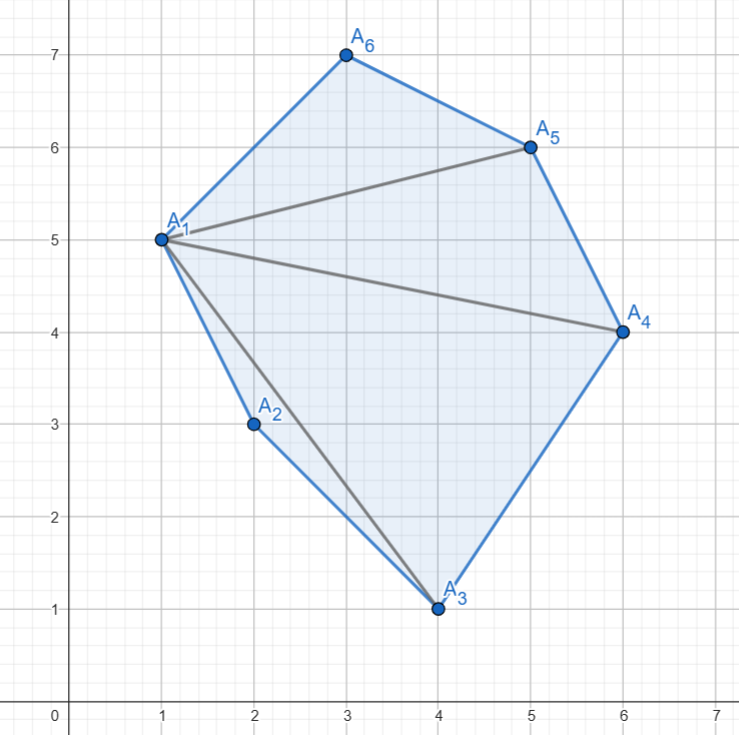
Bây giờ, hình đa giác đã chuyển thành một loạt các tam giác. Mà tam giác thì số công thức tính diện tích nhiều vô kể:
- , trong đó là khoảng cách từ điểm đến đường thẳng .
- , với là nửa chu vi của tam giác
- , trong đó là phép nhân có hướng hai vector
- , với là bán kính đường tròn nội tiếp tam giác (nếu bạn tính được nó).
- ...
Sau khi áp dụng các công thức để tính diện tích tam giác, việc còn lại chỉ là cộng các kết quả lại. Tổng nhận được chắc chắn là diện tích của đa giác cần tính.
Trong các công thức trên, hai công thức đầu ít nhiều phải sử dụng phép căn bậc hai, còn công thức thứ ba với phép toán vector thì đơn giản hơn cả. Khi các đỉnh của đa giác được cho ngược chiều kim đồng hồ, ta có thể bỏ giá trị tuyệt đối của công thức trên:
Đến đây, ta đã có một công thức khá đẹp để tính diện tích đa giác. Tuy nhiên, ta vẫn có thể tiếp tục biến đổi để có công thức đẹp hơn. Ta thấy với và , nhận giá trị bằng . Vì vậy:
Ta áp dụng lại phép chia đa giác và tính diện tích, nhưng lần này với các đỉnh từ đến và thu được các đẳng thức giống như . Cộng các kết quả trên lại, ta được:
Suy ra:
Trong trường hợp các đỉnh được cho theo thứ tự ngược lại, sẽ phải viết lại thành
Hoàn toàn tương tự, ta biến đổi được thành công thức giống như :
Như vậy, diện tích của một đa giác với các đỉnh được cho lần lượt theo thứ tự, không phân biệt cùng chiều hay ngược chiều kim đồng hồ là:
Công thức này được gọi là công thức tam giác.
Người ta cũng hay viết thành dạng định thức như sau:
Do khi tính định thức, ta lấy tổng của các hiệu giữa hai phần tử chéo nhau, người ta cũng gọi công thức tam giác là công thức Shoelace (Shoelace Formula) (shoelace nghĩa là dây giày).
Công thức tam giác cũng có thể biến đổi một lần nữa thành dạng vector:
trong đó là gốc toạ độ.
¶ Công thức hình thang
Bằng một hướng tiếp cận khác, chúng ta cũng có công thức sau:
Định lý: Diện tích đa giác với các đỉnh được sắp xếp theo thứ tự cùng chiều hoặc ngược chiều kim đồng hồ là:
Công thức được gọi là công thức hình thang (Trapezoid Formula).
Về cơ bản, nếu ta khai triển công thức hình thang, ta vẫn sẽ thu được công thức tam giác. Tuy nhiên, có một cách chứng minh chỉ sử dụng phép chia hình và diện tích của những hình cơ bản, bạn đọc tham khảo bên dưới.
Chứng minh (nhấn để hiện)
Xét trường hợp các đỉnh được cho ngược chiều kim đồng hồ. Với mọi , gọi là hình chiếu của lên trục hoành . Khi đó có các tình huống sau xảy ra:
Trường hợp 1: có không quá 1 giao điểm với các cạnh của đa giác
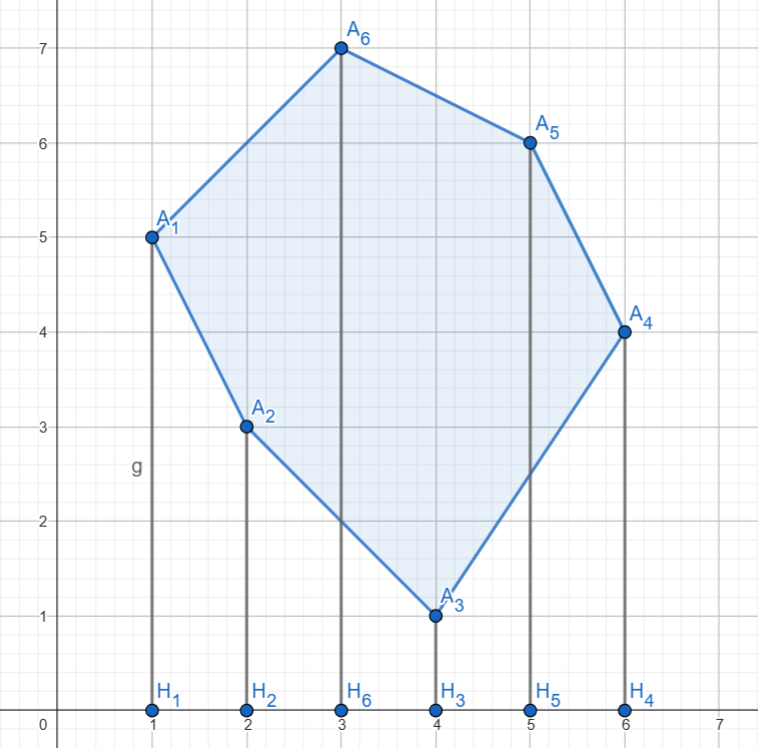
Xét hình thang (đây là hình thang vì song song với do cùng vuông góc với ). Diện tích hình thang trên là:
Hoàn toàn tương tự, ta tính được diện tích của các hình thang :
Ta có thể thấy trên đa giác, tồn tại một điểm nào đó sao cho, với và với , do các điểm đã được sắp theo thứ tự ngược chiều kim đồng hồ. Như vậy, diện tích đa giác đã cho bằng hiệu giữa diện tích đa giác (phần phía trên) và đa giác (phần phía dưới). Diện tích của hai đa giác này lại được tính bằng tổng diện tích các hình thang. Như vậy, diện tích đa giác được tính như sau:
Trường hợp 2: có 2 giao điểm với các cạnh của đa giác
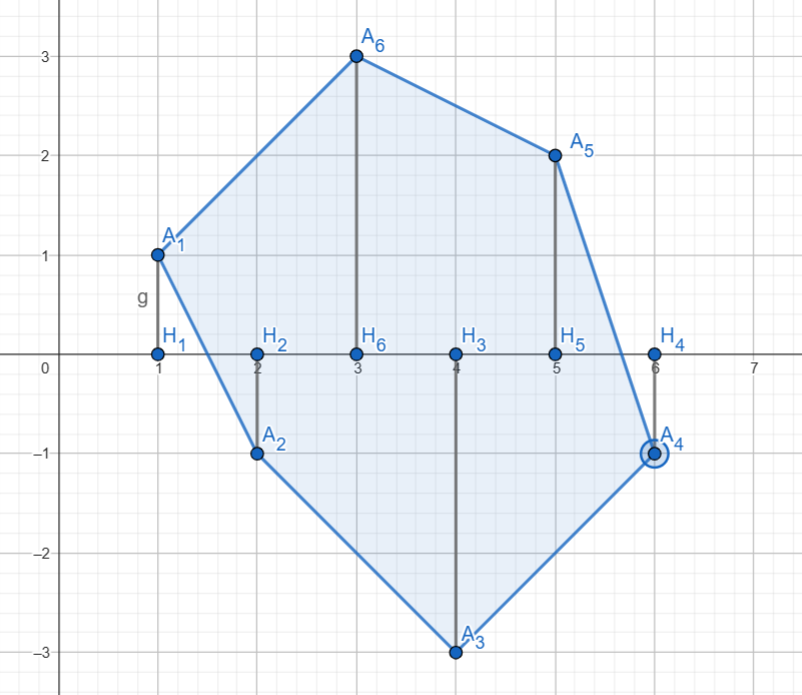
Giả sử giá trị nhỏ nhất trong tất cả các điểm là . Ta tịnh tiến đa giác theo vector có toạ độ , trong đó . Tức là, ta biến đa giác thành đa giác , trong đó có toạ độ là . Do , có thể khẳng định mọi giá trị đều dương. Như vậy, đa giác không có cạnh nào cắt trục . Theo trường hợp thứ nhất, diện tích của đa giác mới tạo thành là:
Ta cũng biết rằng, phép tịnh tiến tạo ra hình mới bằng với hình cũ, và diện tích của chúng là giống nhau. Vậy diện tích hình là .
Như vậy, trong cả hai trường hợp, diện tích của đa giác với các đỉnh được cho ngược chiều kim đồng hồ được tính theo công thức sau:
Hoàn toàn tương tự, khi các đỉnh được cho cùng chiều kim đồng hồ, diện tích của đa giác là:
Hai công thức trên đều cho kết quả không âm. Vậy ta có điều phải chứng minh.
Chú ý: Cách chứng minh trên mô phỏng phép tính tích phân. Sử dụng phép tính tích phân, chứng minh trên sẽ còn đơn giản hơn nữa.
¶ Cài đặt
Dưới đây là cài đặt của công thức tam giác :
double Polygon::area() {
long long s = 0;
for (int i = 0; i < nVertices; i ++) {
int i1 = (i + 1) % nVertices;
s += 1ll * vertices[i].x * vertices[i1].y
- 1ll * vertices[i].y * vertices[i1].x;
}
return abs(1.0 * s / 2);
}
Nếu nộp thử đoạn code trên, ta sẽ thấy kết quả chưa được đẹp lắm. Về mặt lý thuyết, phương pháp này không có gì sai. Vấn đề nằm ở kiểu dữ liệu double. Đối với kiểu này, các số được biểu diễn dưới dạng dấu phẩy động , bao gồm 1 bit dấu , 11 bit cho phần luỹ thừa và 52 bit cho phần sau dấu thập phân. Với số lượng bit để biểu diễn phần thập phân hạn chế như vậy, ta không thể biểu diễn chính xác tất cả các số trên miền giá trị của kết quả. Chẳng hạn, xét tam giác có toạ độ các đỉnh là , , , diện tích của nó sẽ là . Số này muốn biểu diễn chính xác ở dạng số nguyên phải dùng tới 61 bit (chưa tính dấu), do vậy ta không thể có kết quả đúng tới từng chữ số bằng double được.long double có vẻ cũng là một lựa chọn, tuy nhiên trên phần lớn hệ máy, đó cũng chỉ là double mà thôi.
Để ý thấy hai lần diện tích của đa giác là một số nguyên. Lợi dụng điều đó, với bài toán yêu cầu in ra chính xác diện tích đa giác, ta làm như sau:
long long Polygon::area2() {
long long s = 0;
for (int i = 0; i < nVertices; i ++) {
int i1 = (i + 1) % nVertices;
s += 1ll * vertices[i].x * vertices[i1].y
- 1ll * vertices[i].y * vertices[i1].x;
}
return abs(s);
}
int main() {
Polygon plg;
// ...
auto s = plg.area2();
cout << s / 2 << "." << 5 * (s % 2);
return 0;
}
Nếu bạn thích dùng tích có hướng như công thức thì có thể làm như sau:
long long Polygon::area2() {
long long s = 0;
Point o(0, 0);
for (int i = 0; i < nVertices; i ++) {
int i1 = (i + 1) % nVertices;
Vector vi(o, vertices[i]);
Vector vi1(o, vertices[i1]);
s += (vi ^ vi1);
}
return abs(s);
}
¶ Đánh giá
Rất dễ dàng để nhận ra rằng độ phức tạp về cả không gian và thời gian cần để cài đặt tất cả các công thức đã nói trên là
¶ Chú ý
- Trong các ví dụ trên, các điểm đã được cho theo đúng thứ tự tạo thành các đỉnh của đa giác lồi. Nếu các điểm không được cho theo một thứ tự nào cả và biết rằng đa giác cần tính diện tích là đa giác lồi, thì ta cần sắp xếp chúng theo thứ tự bằng các thuật toán tìm bao lồi.
- Các công thức tam giác , , và công thức hình thang vẫn đúng với đa giác không lồi và không tự cắt. Bạn đọc có thể thử tự chứng minh các khẳng định này.
- Khi cài đặt các công thức diện tích trên với bài toán có toạ độ nguyên, để hạn chế tối đa làm việc với số thực, ta thường chỉ dừng lại ở việc tính hai lần diện tích, và nếu được hỏi thì mới lấy kết quả sau khi chia cho , giống như cách cài đặt ở trên
¶ Vị trí tương đối của điểm và đa giác
C.Jordan đã chứng minh rằng: Mọi đa giác không tự cắt đều chia mặt phẳng thành hai miền, một miền bên trong đa giác và một miền bên ngoài đa giác. Như vậy, một điểm có thể nằm ở một trong ba vị trí tương đối sau với một đa giác:
- Nằm trong đa giác
- Nằm ngoài đa giác
- Nằm trên cạnh của đa giác
enum PointPolygonPosition {
INSIDE, // điểm nằm trong đa giác
OUTSIDE, // điểm nằm ngoài đa giác
BOUNDARY // điểm nằm trên cạnh đa giác
};
Bài toán: Cho đa giác đỉnh không tự cắt, điểm thứ có toạ độ theo thứ tự ngược chiều kim đồng hồ. Cho điểm , với mỗi điểm hãy kiểm tra xem điểm này nằm trong, nằm trên cạnh hay nằm ngoài đa giác, biết rằng:
a) Đa giác đã cho là đa giác lồi
b) Đa giác đã cho là đa giác không tự cắt bất kỳ (tức là có thể không lồi)
¶ Trường hợp đa giác lồi
Để thực hành trường hợp này, bạn đọc tham khảo bài Codeforces - Theodore Roosevelt.
¶ Kiểm tra bằng diện tích
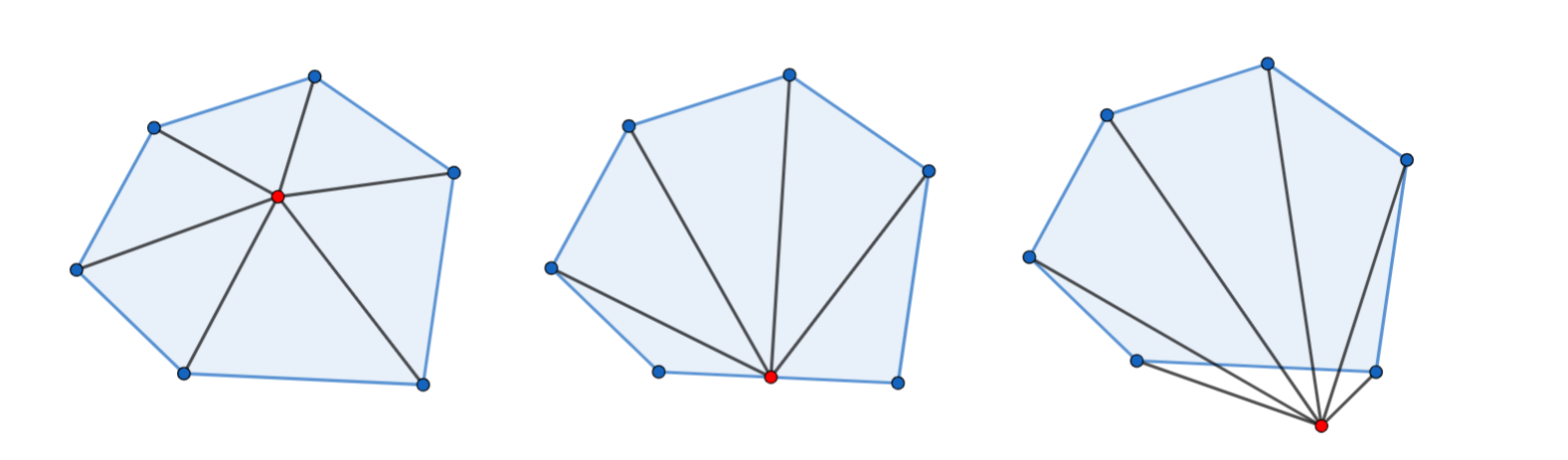
Kiểm tra bằng diện tích là phương pháp đơn giản nhất để xem một điểm có nằm trong đa giác không.
Với mỗi điểm , nối với các đỉnh của tam giác. Ta tính tổng diện tích các tam giác . Sẽ có các trường hợp sau xảy ra (xem hình minh hoạ ở trên để hiểu rõ hơn):
- Nếu tổng trên có diện tích bằng đúng diện tích đa giác, và tất cả các tam giác đều có diện tích khác , ta kết luận điểm nằm bên trong đa giác
- Nếu tổng trên có diện tích bằng đúng diện tích đa giác, và trong số các tam giác tồn tại ít nhất một tam giác có diện tích bằng thì ta kết luận điểm nằm trên một cạnh của đa giác
- Nếu tổng trên khác diện tích của đa giác thì ta kết luận điểm nằm ngoài đa giác.
PointPolygonPosition position(Polygon plg, Point p) {
long long sSumTris = 0;
for (int i = 0; i < plg.nVertices; i++) {
int i1 = (i + 1) % plg.nVertices;
Polygon tri(p, plg.vertices[i], plg.vertices[i1]);
auto sTri = tri.area2();
if (!sTri) {
return BOUNDARY;
}
sSumTris += sTri;
}
return (sSumTris == plg.area2() ? INSIDE : OUTSIDE);
}
Cách kiểm tra này có độ phức tạp không gian là , còn độ phức tạp thời gian là .
¶ Kiểm tra bằng cách chia nhị phân
Do đa giác đã cho là đa giác lồi, nên nếu một điểm nằm trong đa giác, sẽ xảy ra hai trường hợp:
- Tồn tại một giá trị để nằm trong hoặc nằm trên cạnh của tam giác
- Điểm nằm trên cạnh .
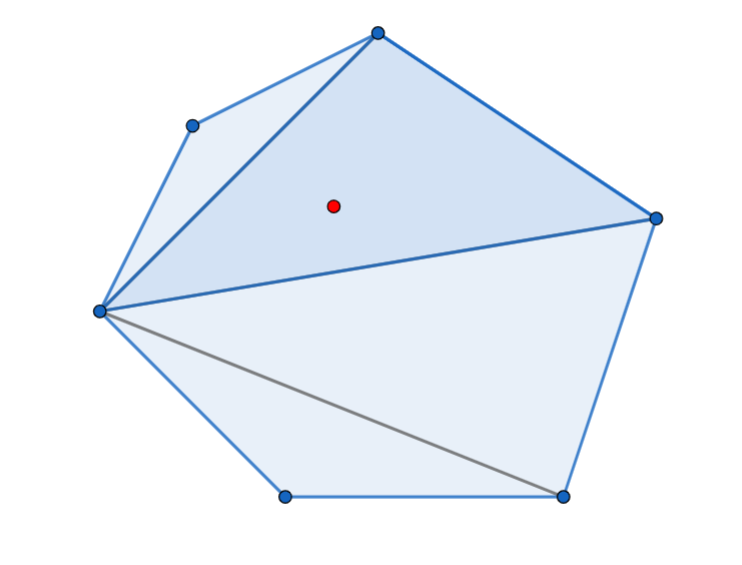
Ta có thể dễ dàng kiểm tra trường hợp thứ hai bằng cách kiểm tra xem hai vector và có cùng phương không (hoặc bất kỳ cách nào bạn thích để kiểm tra ba điểm thẳng hàng).
Xét trường hợp thứ nhất. Ta biết tất cả các đỉnh của đa giác được sắp xếp theo thứ tự ngược chiều kim đồng hồ. Do vậy, nếu điểm nằm bên trong đa giác, sẽ tồn tại một đỉnh () của đa giác để nằm trong góc . Lúc này, các vector ứng với các đường chéo từ đến sẽ nằm bên trái hoặc cùng phương với , và các vector ứng với các đường chéo còn lại nằm bên phải . Tính chất này làm ta nghĩ ngay đến việc sử dụng chia nhị phân để tìm kiếm điểm nói trên.
Về kiểm tra tính chất "trái, phải", ta sử dụng phép nhân có hướng vector (xem phần 2 của series này)
- " nằm bên trái hoặc cùng phương với " đồng nghĩa với " nằm ngược chiều kim đồng hồ hoặc thẳng hàng", tương đương với điều kiện
- " nằm bên phải " đồng nghĩa với " nằm cùng chiều kim đồng hồ", tương đương với điều kiện
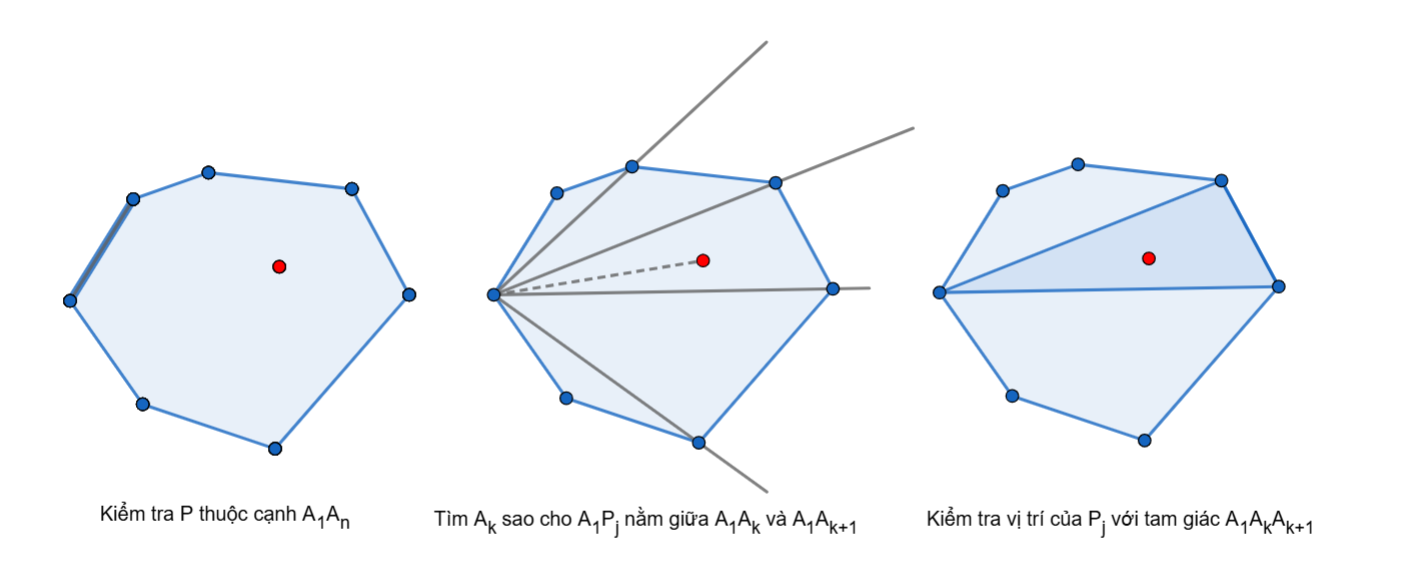
Tóm lại, để kiểm tra vị trí tương đối của một điểm , ta làm như sau:
- Kiểm tra có nằm trên đường thẳng không. Nếu có, kết luận nằm trên cạnh nếu nó nằm giữa hoặc trùng với và , hoặc nằm ngoài đa giác nếu nó không nằm giữa hai điểm trên. Nếu không, tiếp tục sang bước thứ hai.
- Với mỗi điểm , tìm số nhỏ nhất sao cho nằm bên trái hoặc trùng với , sử dụng tìm kiếm nhị phân và tích có hướng. Nếu đã được sắp xếp theo thứ tự ngược chiều kim đồng hồ với , có thể sử dụng phương pháp hai con trỏ. Nếu không có số như vậy thì kết luận nằm ngoài đa giác.
- Kiểm tra xem điểm có nằm trên cạnh không, nếu có thì kết luận điểm nằm trên cạnh của đa giác. Nếu không, kiểm tra xem điểm có nằm trong tam giác không, nếu nằm bên trong thì ta kết luận nằm trong đa giác, còn nếu không thì ta kết luận nằm ngoài đa giác.
bool isCW(Point a, Point b, Point c) {
return (Vector(a, b) ^ Vector(a, c)) < 0;
}
PointPolygonPosition position(Polygon plg, Point p) {
// Kiểm tra P có thuộc A1An không
Vector pa1(p, plg.vertices[0]);
Vector pan(p, plg.vertices[plg.nVertices - 1]);
if (pa1 ^ pan == 0) {
if (1ll * pa1.x * pan.x <= 0) {
return BOUNDARY;
}
return OUTSIDE;
}
// Tìm kiếm nhị phân điểm k
int l = 1, r = plg.nVertices;
while (r - l > 1) {
int mid = (l + r) >> 1;
if (isCW(plg.vertices[0], p, plg.vertices[mid])) {
l = mid;
} else {
r = mid;
}
}
int k = l;
if (k == plg.nVertices - 1) {
return OUTSIDE;
}
// Kiểm tra xem P có thuộc tam giác không
if (Vector(p, plg.vertices[k]) ^ Vector(p, plg.vertices[k + 1]) == 0) {
return BOUNDARY;
}
long long ss = 0;
ss += Polygon(p, plg.vertices[0], plg.vertices[k]).area2();
ss += Polygon(p, plg.vertices[k], plg.vertices[k + 1]).area2();
ss += Polygon(p, plg.vertices[k + 1], plg.vertices[0]).area2();
if (ss == Polygon(plg.vertices[0], plg.vertices[k],
plg.vertices[k + 1]).area2()) {
return INSIDE;
}
return OUTSIDE;
}
Cách làm trên có độ phức tạp không gian là và độ phức tạp thời gian là . Nếu được phép xử lý offline và sử dụng hai con trỏ, độ phức tạp không gian và thời gian lần lượt chuyển thành và .
¶ Trường hợp đa giác không tự cắt bất kỳ
Để thực hành trường hợp này, bạn đọc tham khảo bài CSES - Point in Polygon.
Nếu đa giác có "góc lõm", hai phương pháp trên sẽ không sử dụng được nữa.
Đề kiểm tra điểm thuộc miền trong hay ngoài đa giác đơn (không tự cắt), có một thuật toán rất nổi tiếng. Đó là thuật toán chiếu tia (ray casting). Theo đó, từ mỗi điểm , ta dựng một tia theo một hướng bất kỳ. Sau đó, ta đếm số giao điểm của tia này với các cạnh thuộc đa giác. Nếu số giao điểm là chẵn, điểm này bên ngoài đa giác, ngược lại nó nằm trong đa giác. Trường hợp điểm thuộc cạnh đa giác được xét riêng.
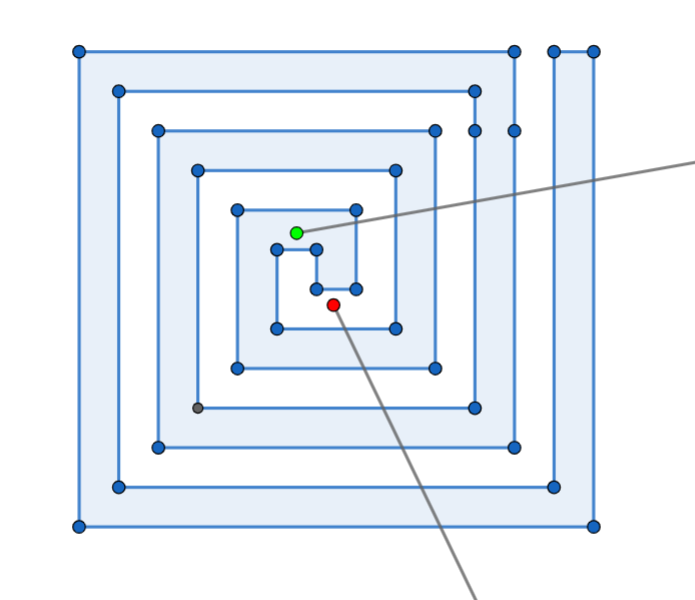
Với dữ kiện đầu vào của bài toán, các đỉnh của đa giác đã được cho theo thứ tự. Như vậy, ta chỉ cần duyệt qua toàn bộ các cặp đỉnh để đểm số giao điểm. Về phần điểm , ta sẽ sử dụng tia theo phương song song với trục hoành, chiều hướng về chiều dương.
Giả sử ta có tia . Tia sẽ cắt cạnh nếu nằm giữa hai đoạn thẳng và . Ta chỉ cần kiểm tra xem , và có cùng hướng (theo chiều kim đồng hồ) với thứ tự cho các điểm của đa giác không là được.
Khi chiếu tia , sẽ có thể xảy ra khả năng tia này đi qua một đỉnh của đa giác. Trong trường hợp này, ta có thể hình dung tia của ta bị dịch lên trên một khoảng rất nhỏ, và do vậy chỉ giao điểm của tia với cạnh nằm phía dưới (ứng với đỉnh có tung độ nhỏ hơn) được xét.
PointPolygonPosition position(Polygon plg, Point p) {
bool isIn = false;
for (int i = 0; i < plg.nVertices; i++) {
int i1 = (i + 1) % plg.nVertices;
auto vpi = Vector(p, plg.vertices[i]);
auto vpj = Vector(p, plg.vertices[i1]);
// Trường hợp nằm trên cạnh
if ((vpi ^ vpj) == 0) {
int xl = min(plg.vertices[i].x, plg.vertices[i1].x);
int xh = max(plg.vertices[i].x, plg.vertices[i1].x);
int yl = min(plg.vertices[i].y, plg.vertices[i1].y);
int yh = max(plg.vertices[i].y, plg.vertices[i1].y);
if (p.x >= xl && p.x <= xh && p.y >= yl && p.y <= yh) {
return BOUNDARY;
}
}
// Trường hợp các đỉnh của đa giác ngược chiều kim đồng hồ
// Chú ý rằng chỉ có một bên của bất đẳng thức có dấu bằng
isIn ^= (plg.vertices[i].y <= p.y
&& p.y < plg.vertices[i1].y && (vpi ^ vpj) > 0);
// Trường hợp các đỉnh của đa giác cùng chiều kim đồng hồ
isIn ^= (plg.vertices[i1].y <= p.y
&& p.y < plg.vertices[i].y && (vpj ^ vpi) > 0);
}
if (isIn) {
return INSIDE;
}
return OUTSIDE;
}
Độ phức tạp của cài đặt trên là về không gian và về thời gian.
¶ Số điểm nguyên nằm trong đa giác
Bài toán: CSES - Polygon Lattice Points
Tóm tắt đề bài: Cho đa giác với các đỉnh có toạ độ nguyên cho trước. Đếm số điểm có toạ độ nguyên nằm bên trong và trên các cạnh của đa giác.
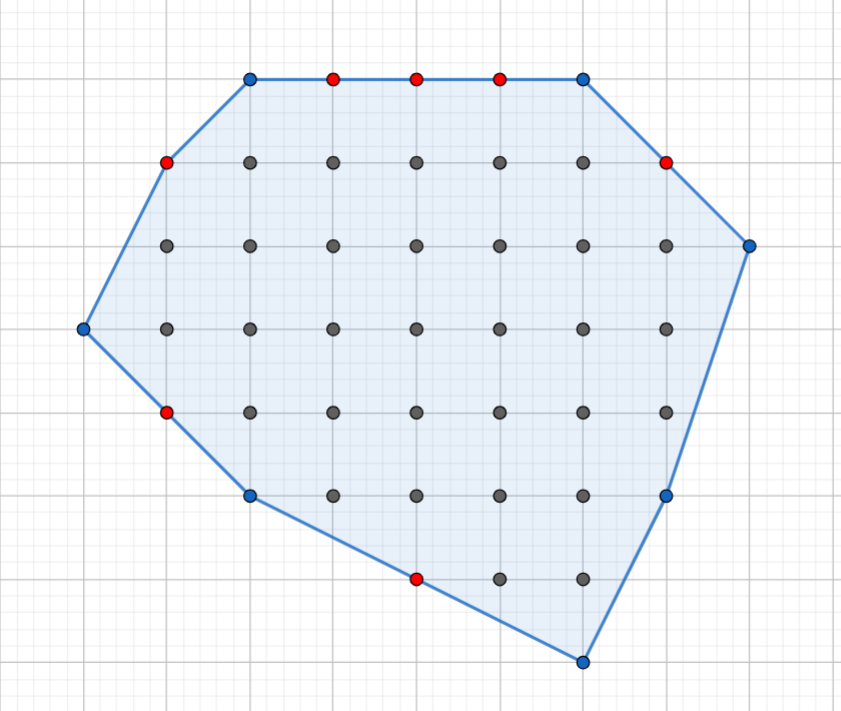
¶ Đếm số điểm nguyên nằm trên cạnh của đa giác
Xét đường thẳng đi qua hai điểm và . Phương trình đường thẳng trên có dạng:
Khi nguyên, để nguyên thì . Để điều này xảy ra thì phải là các bội của . Có giá trị nằm giữa và thoả mãn tính chất trên.
Như vậy, số điểm nguyên nằm trên mỗi cạnh (chỉ tính một đầu mút) sẽ là . Cộng các kết quả này lại ta sẽ được số điểm nguyên trên cạnh của đa giác.
Lưu ý: Về mặt định nghĩa, ta vẫn có với mọi cùng khác . Tuy nhiên, khi cài đặt, kết quả của phép toán có thể là âm nếu ta dùng thuật toán Euclid hoặc hàm __gcd(). Do đó, để chắc chắn có một kết quả dương, ta sẽ sử dụng giá trị
¶ Định lý Pick và số điểm nguyên nằm trong đa giác
Định lý Pick: Cho một đa giác không tự cắt với các đỉnh có toạ độ nguyên và diện tích khác không. Gọi diện tích đa giác là , số điểm nguyên nằm bên trong đa giác là và số điểm nguyên nằm trên cạnh đa giác là . Khi đó diện tích đa giác là:
Do độ dài của bài viết cũng như độ dài của chứng minh, tác giả sẽ không trình bày phần chứng minh trong bài viết này. Bạn đọc tham khảo chứng minh ở đây.
Trong , ta đã tính được ở phần trên, và tính được bằng công thức tam giác . Ngay lập tức ta suy ra được .
¶ Cài đặt
Tác giả cũng sẽ không trình bày cài đặt cho bài toán này do độ dài của bài viết.
Độ phức tạp không gian cần cho bài toán này là . Về thời gian, ta mất để tính diện tích (sử dụng các công thức đã được nói ở trên), cho việc đếm số điểm trên cạnh, và để đếm số điểm trong đa giác. Tổng cộng là .
¶ Bài tập áp dụng
- CSES - Polygon Area
- Codeforces - Very simple problem
- VNOJ - Growing Carrot
- VNOJ - Maximum Triangle Area
- VNOJ - Câu chuyện người lính