¶ BFS (Breadth-first search)
Nguồn: CP-Algorithms, Giải thuật và lập trình - Lê Minh Hoàng
Biên soạn:
- Nguyễn Châu Khanh - VNU University of Engineering and Technology (VNU-UET)
Reviewer:
- Trần Quang Lộc - ITMO University
- Hoàng Xuân Nhật - VNUHCM-University of Science
- Trần Xuân Bách - HUS High School for Gifted Students
¶ Thuật toán duyệt đồ thị ưu tiên chiều rộng
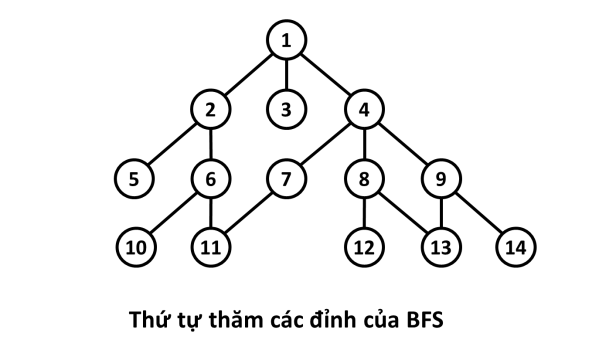
Thuật toán duyệt đồ thị ưu tiên chiều rộng (Breadth-first search - BFS) là một trong những thuật toán tìm kiếm cơ bản và thiết yếu trên đồ thị. Mà trong đó, những đỉnh nào gần đỉnh xuất phát hơn sẽ được duyệt trước.
Ứng dụng của có thể giúp ta giải quyết tốt một số bài toán trong thời gian và không gian tối thiểu. Đặc biệt là bài toán tìm kiếm đường đi ngắn nhất từ một đỉnh gốc tới tất cả các đỉnh khác. Trong đồ thị không có trọng số hoặc tất cả trọng số bằng nhau, thuật toán sẽ luôn trả ra đường đi ngắn nhất có thể. Ngoài ra, thuật toán này còn được dùng để tìm các thành phần liên thông của đồ thị, hoặc kiểm tra đồ thị hai phía, ...
¶ Ý tưởng
Với đồ thị không trọng số và đỉnh nguồn . Đồ thị này có thể là đồ thị có hướng hoặc vô hướng, điều đó không quan trọng đối với thuật toán.
Có thể hiểu thuật toán như một ngọn lửa lan rộng trên đồ thị:
- Ở bước thứ , chỉ có đỉnh nguồn đang cháy.
- Ở mỗi bước tiếp theo, ngọn lửa đang cháy ở mỗi đỉnh lại lan sang tất cả các đỉnh kề với nó.
Trong mỗi lần lặp của thuật toán, "vòng lửa" lại lan rộng ra theo chiều rộng. Những đỉnh nào gần hơn sẽ bùng cháy trước.
Chính xác hơn, thuật toán có thể được mô tả như sau:
- Đầu tiên ta thăm đỉnh nguồn .
- Việc thăm đỉnh sẽ phát sinh thứ tự thăm các đỉnh kề với (những đỉnh gần nhất). Tiếp theo, ta thăm đỉnh , khi thăm đỉnh sẽ lại phát sinh yêu cầu thăm những đỉnh kề với . Nhưng rõ ràng những đỉnh này “xa” hơn những đỉnh nên chúng chỉ được thăm khi tất cả những đỉnh đều đã được thăm. Tức là thứ tự thăm các đỉnh sẽ là:
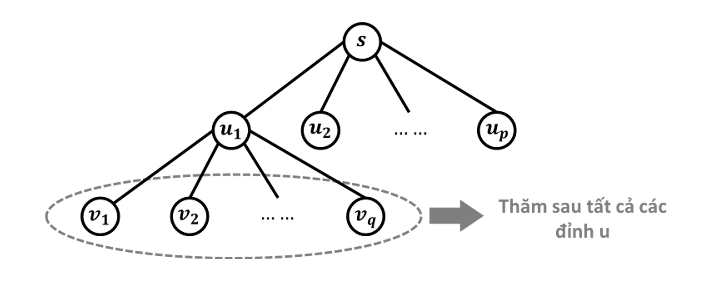
Thuật toán tìm kiếm theo chiều rộng sử dụng một danh sách để chứa những đỉnh đang “chờ” thăm. Tại mỗi bước, ta thăm một đỉnh đầu danh sách, loại nó ra khỏi danh sách và cho những đỉnh kề với nó chưa được thăm xếp hàng vào cuối danh sách. Thuật toán sẽ kết thúc khi danh sách rỗng.
¶ Thuật toán
Thuật toán sử dụng một cấu trúc dữ liệu hàng đợi (queue) để chứa các đỉnh sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
Bước 1: Khởi tạo
- Các đỉnh đều ở trạng thái chưa được đánh dấu. Ngoại trừ đỉnh nguồn đã được đánh dấu.
- Một hàng đợi ban đầu chỉ chứa phần tử là .
Bước 2: Lặp lại các bước sau cho đến khi hàng đợi rỗng:
- Lấy đỉnh ra khỏi hàng đợi.
- Xét tất cả những đỉnh kề với mà chưa được đánh dấu, với mỗi đỉnh đó:
- Đánh dấu đã thăm.
- Lưu lại vết đường đi từ đến .
- Đẩy vào trong hàng đợi (đỉnh sẽ chờ được duyệt tại những bước sau).
Bước 3: Truy vết tìm đường đi.
¶ Mô tả
- Xét đồ thị sau đây, với đỉnh nguồn :
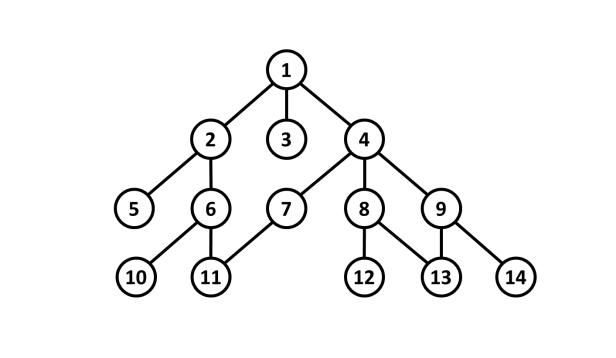
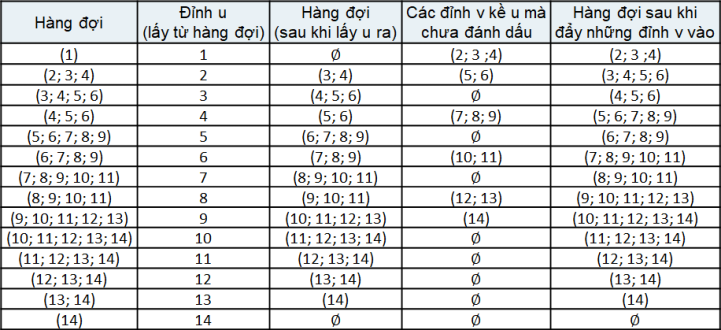
- Quá trình:
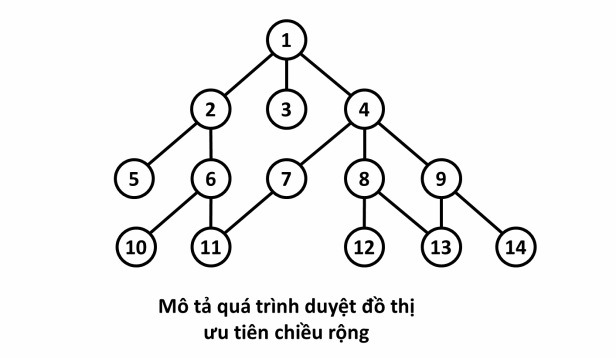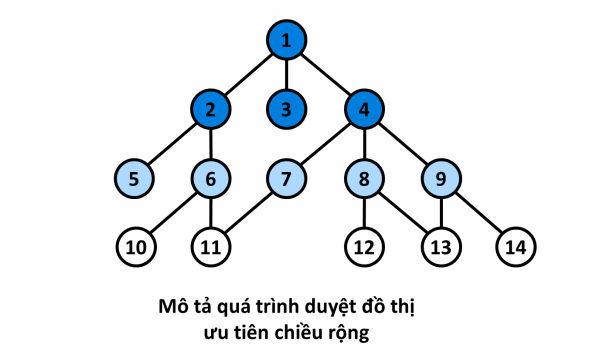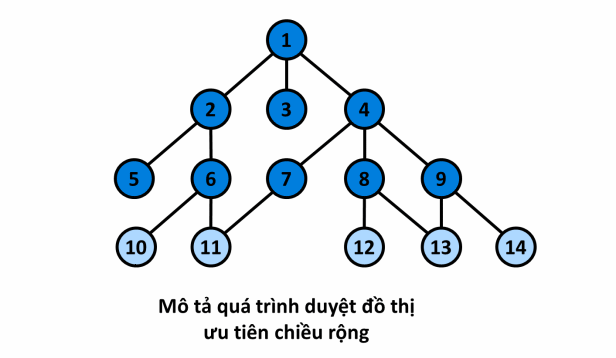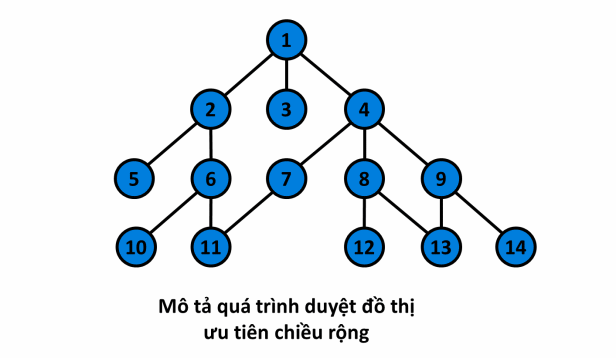
¶ Cài đặt
Cấu trúc dữ liệu:
- Biến
maxN- Kích thước mảng. - Mảng
d[]- Mảng lưu lại khoảng cách từ đỉnh nguồn đến mọi đỉnh. - Mảng
par[]- Mảng lưu lại vết đường đi. - Mảng
visit[]- Mảng đánh dấu các đỉnh đã thăm. - Vector
g[]- Danh sách cạnh kề của mỗi đỉnh. - Hàng đợi
q- Chứa các đỉnh sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
int n; // Số lượng đỉnh của đồ thị
int d[maxN], par[maxN];
bool visit[maxN];
vector <int> g[maxN];
void bfs(int s) { // Với s là đỉnh xuất phát (đỉnh nguồn)
fill_n(d, n + 1, 0);
fill_n(par, n + 1, -1);
fill_n(visit, n + 1, false);
queue <int> q;
q.push(s);
visit[s] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
for (auto v : g[u]) {
if (!visit[v]) {
d[v] = d[u] + 1;
par[v] = u;
visit[v] = true;
q.push(v);
}
}
}
}
¶ Truy vết
- Cài đặt truy vết đường đi từ đỉnh nguồn đến đỉnh :
if (!visit[u]) cout << "No path!";
else {
vector <int> path;
for (int v = u; v != -1; v = par[v])
path.push_back(v);
reverse(path.begin(), path.end());
cout << "Path: ";
for (auto v : path) cout << v << ' ';
}
¶ Các đặc tính của thuật toán
Nếu sử dụng một ngăn xếp (stack) thay vì hàng đợi (queue) thì ta sẽ thu được thứ tự duyệt đỉnh của thuật toán tìm kiếm theo chiều sâu (Depth First Search – DFS). Đây chính là phương pháp khử đệ quy của để cài đặt thuật toán trên các ngôn ngữ không cho phép đệ quy.
Định lí: Thuật toán cho ta độ dài đường đi ngắn nhất từ đỉnh nguồn tới mọi đỉnh (với khoảng cách tới đỉnh bằng ).
Trong thuật toán , nếu đỉnh xa đỉnh nguồn hơn đỉnh , thì sẽ được thăm trước.
- Chứng minh: Trong , từ một đỉnh hiện tại, ta luôn đi thăm tất cả các đỉnh kề với nó trước, sau đó thăm tất cả các đỉnh cách nó một đỉnh, rồi các đỉnh cách nó hai đỉnh, v.v... Như vậy, nếu từ một đỉnh khi ta chạy , quãng đường đến đỉnh luôn là quãng đường đi qua ít cạnh nhất.
¶ Định lý Bắt tay (Handshaking lemma)
Định lý: Trong một đồ thị bất kỳ, tổng số bậc của tất cả các đỉnh bằng gấp đôi số cạnh của đồ thị.
-
Mô tả: Cho đồ thị gồm đỉnh và cạnh. Khi đó, tổng tất cả các bậc của đỉnh trong bằng .
Với là số bậc của đỉnh , ta có:-
Ví dụ: Cho đồ thị sau với và
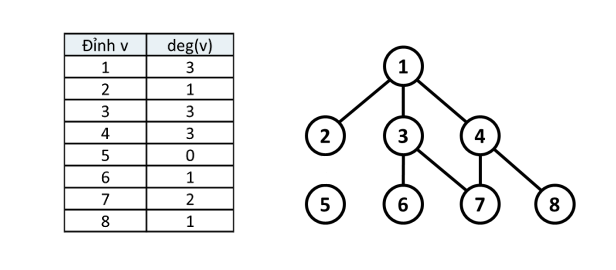
-
-
Chứng minh: Vì mỗi một cạnh nối với đúng hai đỉnh của đồ thị, nên một cạnh sẽ đóng góp đơn vị vào tổng số bậc của tất cả các đỉnh.
Hệ quả: Trong đồ thị, số lượng đỉnh bậc lẻ luôn là một số chẵn.
-
Chứng minh: Gọi và lần lượt là tập các đỉnh bậc lẻ và bậc chẵn của đồ thị . Ta có:
- chẵn
- chẵn
chẵn
Nhận xét:
- Trong quá trình duyệt đồ thị được biểu diễn bằng danh sách kề, mỗi cạnh sẽ được duyệt chính xác hai lần đối với đồ thị vô hướng (vì mỗi cạnh sẽ được lưu trong danh sách kề của đỉnh). Còn đối với đồ thị có hướng, mọi cạnh của đồ thị chỉ được duyệt chính xác một lần.
Tham khảo: Handshaking_lemma
¶ Độ phức tạp thuật toán
¶ Độ phức tạp thời gian
Gọi là số lượng đỉnh và là số lượng cạnh của đồ thị.
Trong quá trình , cách biểu diễn đồ thị có ảnh hưởng lớn tới chi phí về thời gian thực hiện giải thuật :
- Nếu đồ thị biểu diễn bằng danh sách kề (vector
g[]) :- Ta có thể thực hiện thuật toán này một cách tối ưu nhất về mặt thời gian nhờ khả năng duyệt qua các đỉnh kề của mỗi đỉnh một cách hiệu quả.
- Vì ta sử dụng mảng
visit[]để ngăn việc đẩy một đỉnh vào hàng đợi nhiều lần nên mỗi đỉnh sẽ được thăm chính xác một lần duy nhất. Do đó, ta mất độ phức tạp thời gian dành cho việc thăm các đỉnh. - Bất cứ khi nào một đỉnh được thăm, mọi cạnh kề với đỉnh đó đều được duyệt, với thời gian dành cho mỗi cạnh là . Từ phần nhận xét của định lý Bắt tay (Handshaking lemma), ta sẽ mất độ phức tạp thời gian dành cho việc duyệt các cạnh.
- Nhìn chung, độ phức tạp thời gian của thuật toán này là . Đây là cách cài đặt tốt nhất.
- Nếu đồ thị được biểu diễn bằng ma trận kề :
- Ta cũng sẽ mất độ phức tạp thời gian dành cho việc thăm các đỉnh (giải thích tương tự như trên).
- Với mỗi đỉnh được thăm, ta sẽ phải duyệt qua toàn bộ các đỉnh của đồ thị để kiểm tra đỉnh kề với nó. Do đó, thuật toán sẽ mất độ phức tạp .
¶ Độ phức tạp không gian
Tại mọi thời điểm, trong hàng đợi (queue q) có không quá phần tử. Do đó, độ phức tạp bộ nhớ là .
¶ Ứng dụng BFS để xác định thành phần liên thông
¶ Bài toán 1
BDFS - Đếm số thành phần liên thông
¶ Đề bài
Cho đơn đồ thị vô hướng gồm đỉnh và cạnh , các đỉnh được đánh số từ tới . Tìm số thành phần liên thông của đồ thị.
¶ Ý tưởng
Một đồ thị có thể liên thông hoặc không liên thông. Nếu đồ thị liên thông thì số thành phần liên thông của nó là . Điều này tương đương với phép duyệt theo thủ tục được gọi đến đúng một lần. Nếu đồ thị không liên thông (số thành phần liên thông lớn hơn ) ta có thể tách chúng thành những đồ thị con liên thông. Điều này cũng có nghĩa là trong phép duyệt đồ thị, số thành phần liên thông của nó bằng số lần gọi tới thủ tục .
¶ Thuật toán
Thuật toán ứng dụng để xác định thành phần liên thông:
- Bước 0: Khởi tạo số lượng thành phần liên thông bằng .
- Bước 1: Xuất phát từ một đỉnh chưa được đánh dấu của đồ thị. Ta đánh dấu đỉnh xuất phát, tăng số thành phần liên thông thêm .
- Bước 2: Từ một đỉnh đã đánh dấu, ta đánh dấu tất cả các đỉnh kề với mà chưa được đánh dấu.
- Bước 3: Thực hiện bước cho đến khi không còn thực hiện được nữa.
- Bước 4: Nếu số số đỉnh đánh dấu bằng (mọi đỉnh đều được đánh dấu) kết thúc thuật toán và trả về số thành phần liên thông, ngược lại quay về bước .
¶ Mô tả
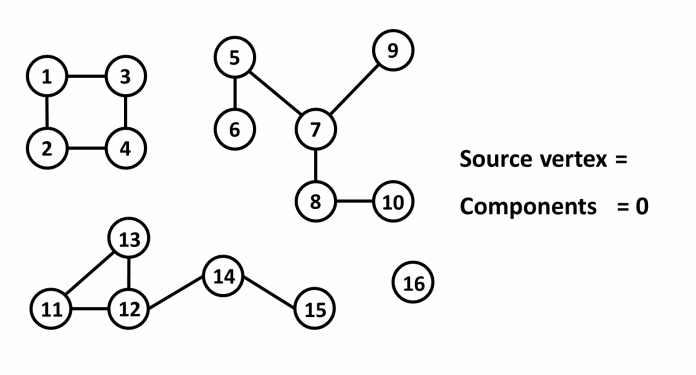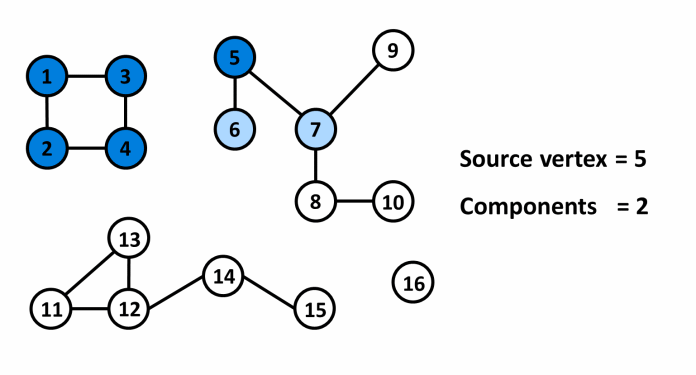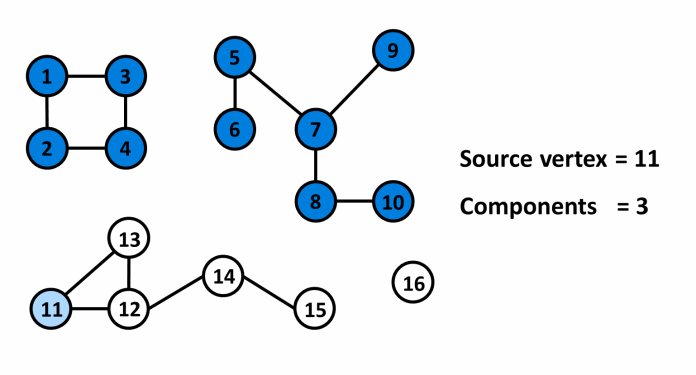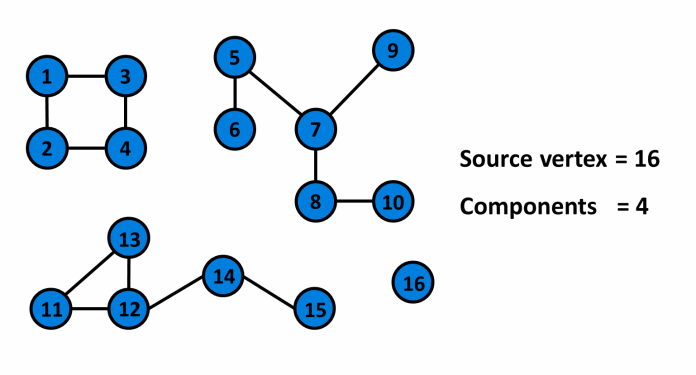
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
maxN = 100007. - Biến
components- Số lượng thành phần liên thông. - Mảng
visit[]- Mảng đánh dấu các đỉnh đã thăm. - Vector
g[]- Danh sách cạnh kề của mỗi đỉnh. - Hàng đợi
q- Chứa các đỉnh sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 1e5 + 7;
int n, m, components = 0;
bool visit[maxN];
vector <int> g[maxN];
void bfs(int s) {
++components;
queue <int> q;
q.push(s);
visit[s] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
for (auto v : g[u]) {
if (!visit[v]) {
visit[v] = true;
q.push(v);
}
}
}
}
int main() {
cin >> n >> m;
while (m--) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
fill_n(visit, n + 1, false);
for (int i = 1; i <= n; ++i)
if (!visit[i]) bfs(i);
cout << components;
}
¶ Đánh giá
Ta cũng có thể sử dụng thuật toán tìm kiếm theo chiều sâu (Depth First Search – DFS) để xác định thành phần liên thông.
Độ phức tạp
Độ phức tạp của thuật toán là .
¶ Thuật toán loang (Flood Fill)
Thuật toán loang (thuật toán vết dầu loang) là một kĩ thuật sử dụng để tìm tất cả các điểm có thể đi tới. Điểm khác biệt giữa Loang so với đa số những bài là ta không phải tìm chi phí nhỏ nhất.
Thuật toán loang được dùng khá nhiều trong tin học, điển hình là thuật toán loang trên ma trận được ứng dụng để đếm số thành phần liên thông trên ma trận. Ngoài ra, nó còn ứng dụng trong các bài toán thực tế như các bài toán tìm đường đi, game dò mìn, game line98,...
Gọi là thuật toán loang vì nguyên lí của thuật toán này rất giống với hiện tượng loang của chất lỏng. Khi ta nhỏ dầu xuống một mặt phẳng, vết dầu có thể loang ra những khu vực xung quanh. Tương tự, thuật toán loang trên ma trận cũng vậy, ta sẽ duyệt một ô trên ma trận và sau đó duyệt các điểm xung quanh nó và loang dần ra để giải quyết bài toán.
¶ Bài toán 2
¶ Đề bài
Một tai nạn hàng hải đã khiến dầu tràn ra biển. Để có được thông tin về mức độ nghiêm trọng của thảm họa này, người ta phải phân tích các hình ảnh chụp từ vệ tinh, từ đó tính toán chi phí khắc phục cho phù hợp. Đối với điều này, số lượng vết dầu loang trên biển và kích thước của mỗi vết loang phải được xác định. Vết loang là một mảng dầu nổi trên mặt nước.
Để tiện cho việc xử lí, hình ảnh được chuyển đổi thành một ma trận nhị phân kích thước . Với là ô bị nhiễm dầu, và là ô không bị nhiễm dầu. Vết dầu loang là tập hợp của một số ô bị nhiễm dầu có chung cạnh.
Họ đã thuê bạn để giúp họ xử lí hình ảnh. Công việc của bạn là đếm số lượng vết loang trên biển và kích thước tương ứng của từng vết.
¶ Ý tưởng
Ta xây dựng một mô hình đồ thị của bài toán như sau:
- Gọi mỗi đỉnh của đồ thị tương ứng với mỗi ô (ô bị nhiễm dầu) của ma trận.
- Tồn tại một cạnh nối giữa cặp đỉnh khi và chỉ khi ô tương ứng với đỉnh kề cạnh với ô tương ứng với đỉnh và cả hai ô đều là ô .
Khi đó, bài toán quy về thành bài toán xác định thành phần liên thông của đồ thị. Trong đó, mỗi thành phần liên thông tương ứng với mỗi một vết dầu loang.
Nghĩa là, số lượng thành phần liên thông của đồ thị chính là số lượng vết dầu loang. Và số lượng đỉnh nằm trong cùng một thành phần liên thông là kích thước của vết loang tương ứng.
¶ Thuật toán
Áp dụng thuật toán loang trên ma trận để xác định thành phần liên thông:
- Khởi tạo số lượng vết dầu bằng .
- Duyệt dần từng ô của ma trận, nếu ô đang xét là một ô bị nhiễm dầu (ô ) và chưa được đánh dấu:
- Đánh dấu lại ô đó.
- Tăng số lượng vết dầu thêm .
- Thực hiện thủ tục xuất phát từ ô đó để loang ra các ô xung quanh như sau:
- Khởi tạo kích thước của vết dầu đang xét là .
- Tiếp tục thực hiện công việc sau cho đến khi không còn thực hiện được nữa: Từ một ô đã đánh dấu, ta đánh dấu tất cả các ô bị nhiễm dầu kề cạnh với ô đó mà chưa được đánh dấu. Mỗi lần đánh dấu lại một ô thì ta tăng kích thước của vết dầu thêm .
- Sử dụng mảng để lưu lại kích thước của từng vết loang.
- Nếu tất cả các ô bị nhiễm dầu đều đã được đánh dấu, trả ra kết quả và kết thúc thuật toán.
¶ Mô tả
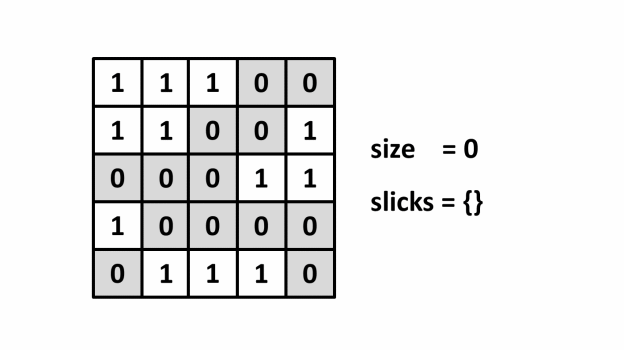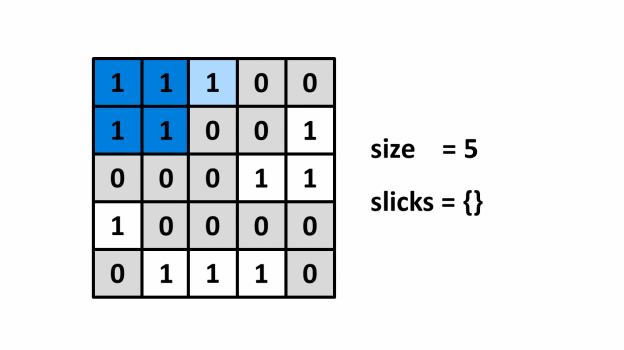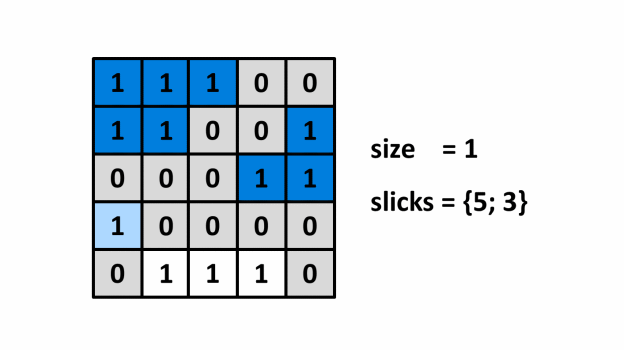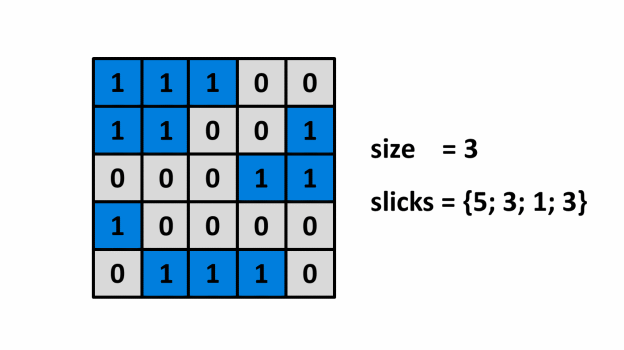
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
maxN = 300. - Mảng
visit[][]- Mảng đánh dấu các ô đã duyệt. - Vector
slicks- Lưu kích thước của mỗi vết dầu loang. - Hàng đợi
q- Chứa các ô sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 300;
int n, m;
bool a[maxN][maxN], visit[maxN][maxN];
vector <int> slicks;
int moveX[] = {0, 0, 1, -1};
int moveY[] = {1, -1, 0, 0};
// Thủ tục cài đặt lại cấu trúc dữ liệu sau mỗi bộ test
void reset() {
slicks.clear();
for (int i = 1; i <= n; ++i)
fill_n(visit[i], m + 1, false);
}
int bfs(int sx, int sy) {
int sizeSlicks = 1; // Biến đếm số lượng đỉnh thuộc thành phần liên thông
queue < pair <int, int> > q;
q.push({sx, sy});
visit[sx][sy] = true;
while (!q.empty()) {
int x = q.front().first;
int y = q.front().second;
q.pop();
for (int i = 0; i < 4; ++i) {
int u = x + moveX[i];
int v = y + moveY[i];
if (u > n || u < 1) continue;
if (v > m || v < 1) continue;
if (a[u][v] && !visit[u][v]) {
++sizeSlicks;
visit[u][v] = true;
q.push({u, v});
}
}
}
return sizeSlicks;
}
int main() {
while (cin >> n >> m) {
if (!n && !m) return 0;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) cin >> a[i][j];
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
if (a[i][j] && !visit[i][j])
slicks.push_back(bfs(i, j));
cout << slicks.size() << '\n';
sort(slicks.begin(), slicks.end());
slicks.push_back(1e9);
int number = 0, pre = slicks[0];
for (auto v : slicks)
if (v != pre) {
cout << pre << ' ' << number << '\n';
pre = v;
number = 1;
}
else ++number;
reset();
}
}
¶ Đánh giá
Ta sử dụng mảng moveX[] và moveY[] để có thể dễ dàng duyệt qua tất cả các ô kề cạnh với ô đang xét.
Độ phức tạp
Với mỗi bộ test:
- Vì mỗi ô của ma trận được duyệt đúng duy nhất lần nên ta sẽ mất độ phức tạp .
- Ta sẽ mất thêm vì ta phải duyệt qua ô kề cạnh với mỗi ô của ma trận.
Nhìn chung, độ phức tạp của thuật toán là . Với là số lượng bộ test.
¶ Bài tập áp dụng
¶ Ứng dụng BFS để tìm đường đi ngắn nhất trong đồ thị không trọng số
Những bài sử dụng thường yêu cầu tìm số bước ít nhất (hoặc đường đi ngắn nhất) từ điểm đầu đến điểm cuối. Bên cạnh đó, đường đi giữa điểm bất kì thường có chung trọng số (và thường là ). Phổ biến nhất là dạng bài cho bảng , có những ô đi qua được và những ô không đi qua được. Bảng này có thể là mê cung, sơ đồ, các thành phố hoặc các thứ các thứ tương đương. Có thể nói đây là những bài toán kinh điển.
Hãy xem xét bài toán sau đây:
¶ Bài toán 3
¶ Đề bài
Cho một bảng hình chữ nhật chia thành lưới ô vuông kích thước (). Mỗi ô mang trong giá trị sau : . , * , B , C. Cô bò Bessie đang đứng ở ô C và cần đi đến ô B. Mỗi bước đi Bessie có thể đi từ ô vuông sang ô vuông khác kề cạnh nhưng không được đi vào ô * hay đi ra khỏi bảng. Hãy tìm số bước đi ít nhất để Bessie đến được ô B.
Đảm bảo chỉ có duy nhất ô B và ô C trong bảng, và luôn tồn tại đường đi từ C đến B.
¶ Phân tích
Theo mối quan hệ được xây dựng trong đề bài, Bessie có thể di chuyển từ ô vuông sang ô vuông khác kề cạnh. Từ đó, ta có thể xây dựng một mô hình đồ thị của bài toán:
- Gọi mỗi đỉnh của đồ thị tương ứng với mỗi ô trong lưới ô vuông.
- Tồn tại một cạnh nối giữa cặp đỉnh khi và chỉ khi từ ô tương ứng với đỉnh có thể di chuyển đến ô tương ứng với đỉnh (đồng nghĩa, ô tương ứng với đỉnh kề cạnh với ô tương ứng với đỉnh và cả ô đều không phải là ô
*).
Sau khi xây dựng được đồ thị, bài toán quy về như sau: Tìm đường đi ngắn nhất từ đỉnh tương ứng với ô C đến đỉnh tương ứng với ô B. Độ dài đường đi ngắn nhất đó chính là số bước ít nhất mà Bessie cần thực hiện.
Vậy để tìm được kết quả bài toán, ta sẽ áp dụng thuật toán .
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
maxN = 110. - Mảng
d[][]- Mảng lưu số bước ít nhất để đi từ ô xuất phát đến mỗi ô khác. - Mảng
visit[][]- Mảng đánh dấu các ô đã đi qua. - Hàng đợi
q- Chứa các ô sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 110;
int r, c;
char a[maxN][maxN];
int d[maxN][maxN];
bool visit[maxN][maxN];
int moveX[] = {0, 0, 1, -1};
int moveY[] = {1, -1, 0, 0};
void bfs(int sx, int sy) {
for (int i = 1; i <= r; ++i) {
fill_n(d[i], c + 1, 0);
fill_n(visit[i], c + 1, false);
}
queue < pair <int, int> > q;
q.push({sx, sy});
visit[sx][sy] = true;
while (!q.empty()) {
int x = q.front().first;
int y = q.front().second;
q.pop();
// Nếu gặp được ô B thì kết thúc thủ tục BFS
if (a[x][y] == 'B') return;
for (int i = 0; i < 4; ++i) {
int u = x + moveX[i];
int v = y + moveY[i];
if (u > r || u < 1) continue;
if (v > c || v < 1) continue;
if (a[u][v] == '*') continue;
if (!visit[u][v]) {
d[u][v] = d[x][y] + 1;
visit[u][v] = true;
q.push({u, v});
}
}
}
}
int main() {
int sx, sy, tx, ty;
cin >> r >> c;
for (int i = 1; i <= r; ++i)
for (int j = 1; j <= c; ++j) {
cin >> a[i][j];
if (a[i][j] == 'C') { sx = i; sy = j; }
if (a[i][j] == 'B') { tx = i; ty = j; }
}
bfs(sx, sy);
cout << d[tx][ty];
}
¶ Đánh giá
Ta sử dụng mảng moveX[] và moveY[] để có thể dễ dàng duyệt qua tất cả các ô kề cạnh với ô đang xét.
Độ phức tạp
Giống như thông thường, độ phức tạp của bài toán là (với là số đỉnh và là số cạnh của đồ thị). Trong đó, số đỉnh của đồ thị bằng số lượng ô vuông của bảng (nghĩa là ). Trong trường hợp tệ nhất, tại mỗi ô đều có thể đi sang ô kề cạnh, nên đồ thị sẽ có khoảng cạnh.
Mặc dù trong quá trình , khi gặp được ô B thì thủ tục kết thúc luôn nên độ phức tạp thực tế có thể ít hơn so với tính toán. Nhưng trong trường hợp tệ nhất là ta phải đi hết tất cả các ô khác xong mới đến được ô B. Nên nhìn chung, độ phức tạp của thuật toán là .
¶ Bài toán 4
¶ Đề bài
Trong một tòa nhà có tầng, các tầng được đánh số từ đến , hiện tại bạn đang đứng tại tầng và cần đi đến tầng . Tại mỗi tầng, thang máy chỉ có nút là "UP u" và "DOWN d" :
- Nút "UP u" có thể đưa bạn lên đúng tầng nếu như có đủ số tầng phía trên.
- Nút "DOWN d" có thể đưa bạn xuống đúng tầng nếu như có đủ số tầng phía dưới.
Trường hợp không có đủ số tầng thì thang máy sẽ không lên hoặc không xuống. Hãy tính số lần phải bấm nút ít nhất để có thể đến được tầng .
.
¶ Phân tích
Ghi chú: Từ ứng dụng tìm đường đi ngắn nhất trong đồ thị không trọng số, ta có thể áp dụng để giải quyết các vấn đề hoặc trò chơi có số lần di chuyển ít nhất, nếu mỗi trạng thái của nó có thể được biểu diễn bằng một đỉnh của đồ thị và việc chuyển đổi từ trạng thái này sang trạng thái khác là các cạnh của đồ thị.
Với bài toán này ta không thể sử dụng thuật toán vét cạn, hay quay lui có điều kiện vì số lượng tầng ở đây có thể lên đến dẫn tới việc chương trình có thể chạy quá thời gian.
Thay vào đó, ta sẽ sử dụng thuật toán . Tư tưởng ở đây là ta sẽ đi tính số lần bấm nút nhỏ nhất để đến được mỗi tầng.
Từ mối quan hệ được xây dựng trong bài toán, ta có thể xây dựng một mô hình đồ thị như sau:
- Gọi mỗi đỉnh của đồ thị tương ứng với mỗi tầng của tòa nhà.
- Nếu từ tầng ta có thể đến được tầng bằng một lần bấm nút thì tồn tại cạnh nối chiều từ đỉnh đến đỉnh . Tương đương với việc tồn tại cạnh (nếu ) và cạnh (nếu ).
Sau khi xây dựng được đồ thị, đường đi ngắn nhất từ đỉnh đến đỉnh chính là số lần bấm nút ít nhất cần thực hiện.
Vậy để tìm được kết quả bài toán, ta sẽ áp dụng thuật toán .
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
maxN = 1000007. - Mảng
number[]- Mảng lưu lại số lần bấm nút ít nhất để đến được mỗi tầng. - Mảng
visit[]- Mảng đánh dấu lại các tầng đã đến. - Hàng đợi
q- Chứa các tầng sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 1e6 + 7;
int f, s, g, u, d;
int visit[maxN], number[maxN];
void bfs() {
fill_n(number, f + 1, 0);
fill_n(visit, f + 1, false);
queue <int> q;
q.push(s);
visit[s] = true;
while (!q.empty()) {
int x = q.front();
q.pop();
// Nếu gặp được tầng đích thì kết thúc thủ tục BFS
if (x == g) return;
for (int y : {x + u, x - d}) {
if (y > f || y < 1) continue;
if (!visit[y]) {
visit[y] = true;
number[y] = number[x] + 1;
q.push(y);
}
}
}
// Kết thúc quá trình BFS mà ko đến được tầng đích
number[g] = -1;
}
int main() {
cin >> f >> s >> g >> u >> d;
bfs();
if (number[g] != -1) cout << number[g];
else cout << "use the stairs";
}
¶ Đánh giá
Độ phức tạp
Độ phức tạp của bài toán là (với là số đỉnh và là số cạnh của đồ thị). Trong đó, số đỉnh của đồ thị bằng số tầng của tòa nhà (nghĩa là ). Đa số mỗi tầng đều có thể đi đến tầng khác, nên đồ thị sẽ có khoảng cạnh.
Nhìn chung, độ phức tạp của thuật toán là .
¶ Bài toán 5
cjpaysballas - CJ thanh toán BALLAS
¶ Đề bài
Cho một đồ thị có hướng gồm đỉnh và cạnh . Các đỉnh được đánh số từ đến . Hãy tìm đường đi ngắn nhất xuất phát tại đỉnh và kết thúc tại đỉnh . Nếu có nhiều đường đi ngắn nhất thỏa mãn, thì chỉ ra đường đi có thứ tự từ điển nhỏ nhất trong số đó.
Đảm bảo luôn tồn tại ít nhất một đường đi từ đến .
¶ Phân tích
Định lí: Nếu ta sắp xếp các danh sách kề của mỗi đỉnh theo thứ tự tăng dần thì thuật toán luôn trả về đường đi có thứ tự từ điển nhỏ nhất trong số những đường đi ngắn nhất.
- Chứng minh: Trong quá trình , nếu các đỉnh được đưa vào hàng đợi (queue) theo thứ tự từ điển tăng dần thì theo cơ chế hoạt động (First In - First Out), các đỉnh có thứ tự từ điển nhỏ hơn sẽ được thăm trước.
Từ định lí trên, ta sẽ sắp xếp lại thứ tự đỉnh kề theo thứ tự tăng dần để đảm bảo đường đi được in ra theo thứ tự từ điển. Sau đó sử dụng kết hợp với truy vết để giải quyết bài toán.
¶ Cài đặt
Cấu trúc dữ liệu:
- Mảng
par[]- Mảng lưu lại vết đường đi. - Mảng
visit[]- Mảng đánh dấu các đỉnh đã thăm. - Vector
g[]- Danh sách cạnh kề của mỗi đỉnh. - Hàng đợi
q- Chứa các đỉnh sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 1e5 + 7;
int n, m, s, t;
int par[maxN];
bool visit[maxN];
vector <int> g[maxN];
void bfs(int s) {
fill_n(par, n + 1, -1);
fill_n(visit, n + 1, false);
queue <int> q;
q.push(s);
visit[s] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
for (auto v : g[u]) {
if (!visit[v]) {
par[v] = u;
visit[v] = true;
q.push(v);
}
}
}
}
int main() {
cin >> n >> m >> s >> t;
while (m--) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
}
// Sắp xếp danh sách kề
for (int i = 1; i <= n; ++i)
sort(g[i].begin(), g[i].end());
bfs(s);
// Truy vết
vector <int> path;
for (int v = t; v != -1; v = par[v])
path.push_back(v);
reverse(path.begin(), path.end());
for (auto v : path) cout << v << ' ';
}
¶ Đánh giá
Độ phức tạp
- Độ phức tạp của thuật toán là .
¶ Bài tập áp dụng
NAKANJ - Minimum Knight moves !!!
NATALIAG - Natalia Plays a Game
MULTII - Yet Another Multiple Problem
Cycle in Maze - 769C Codeforces
Okabe and City - 821D Codeforces
Police Stations - 796D Codeforces
¶ Ứng dụng BFS để tìm chu trình ngắn nhất trong đồ thị có hướng không trọng số
¶ Bài toán 6
¶ Đề bài
Ada đang có một chuyến đi ở Bugindia. Ở đó có nhiều thành phố và những con đường một chiều nối giữa chúng. Ada rất băn khoăn về việc tìm con đường ngắn nhất bắt đầu tại một thành phố và kết thúc ở cùng một thành phố. Vì Ada thích những chuyến đi ngắn, cô ấy đã nhờ bạn tìm độ dài của con đường như vậy cho mỗi thành phố ở Bugindia.
Input
- Dòng đầu tiên chứa số là số lượng thành phố.
- dòng tiếp theo, mỗi dòng chứa số nguyên . Nghĩa là, nếu thì tồn tại một con đường nối từ thành phố đến thành phố . Ngược lại, nếu thì không tồn tại con đường.
Output
- Gồm dòng: Dòng thứ in ra độ dài của con đường ngắn nhất bắt đầu từ thành phố và kết thúc ở thành phố . Nếu không tồn tại con đường nào như vậy, hãy in ra "NO WAY" để thay thế.
¶ Phân tích
Theo yêu cầu đề bài, với mỗi thành phố, ta phải tìm độ dài con đường ngắn nhất bắt đầu và kết thúc ở cùng một thành phố đó.
Ta coi các thành phố là các đỉnh của đồ thị và các con đường chiều là các cạnh có hướng của đồ thị.
Đồng nghĩa với việc, với mỗi đỉnh của đồ thị, ta phải tìm độ dài của chu trình ngắn nhất chứa đỉnh đó. Vì thứ tự duyệt các đỉnh của thuật toán luôn bắt đầu duyệt từ các đỉnh gần đỉnh nguồn nhất cho đến các đỉnh nằm ở xa đỉnh nguồn. Do đó, ta có thể áp dụng tính chất này của để có thể tìm ra đỉnh nằm gần đỉnh nguồn nhất sao cho có cạnh nối từ đến đỉnh nguồn.
Đường đi ngắn nhất từ đỉnh nguồn đến đỉnh , rồi từ trở lại đỉnh nguồn bằng cạnh có hướng, chính là chu trình ngắn nhất chứa đỉnh nguồn.
¶ Mô tả
- Thực hiện bắt đầu tại đỉnh :
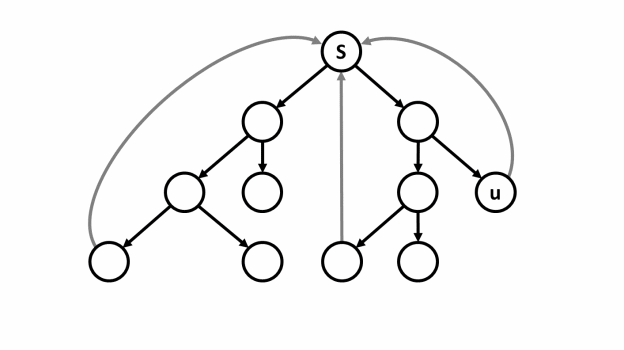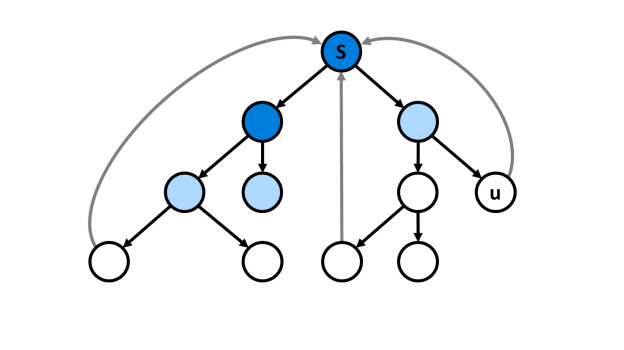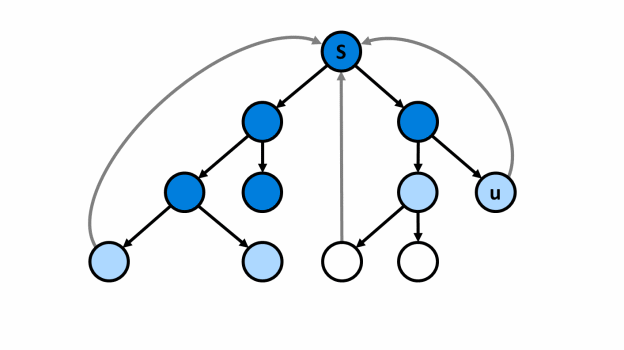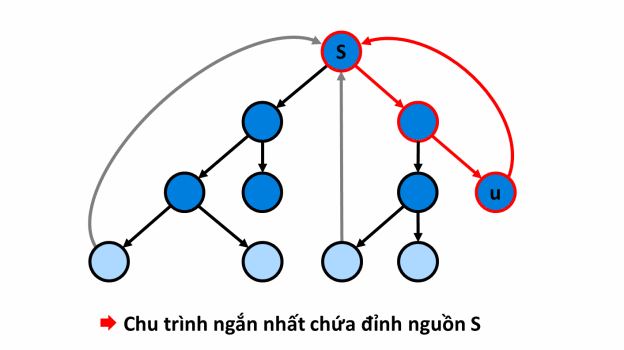
¶ Thuật toán
Với mỗi đỉnh của đồ thị, ta thực hiện bắt đầu từ đỉnh đó.
Trong quá trình , ghi nhận khoảng cách từ đỉnh nguồn đến đỉnh đang duyệt, nếu gặp lại đỉnh nguồn thì đó là chu trình ngắn nhất chứa đỉnh nguồn. Lúc này, ta in ra độ dài chu trình và kết thúc , rồi bắt đầu thực hiện một mới từ đỉnh tiếp theo.
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
maxN = 210. - Mảng
visit[]- Mảng đánh dấu các đỉnh đã thăm. - Mảng
d[]- Mảng lưu lại khoảng cách từ đỉnh nguồn đến mọi đỉnh. - Vector
g[]- Danh sách cạnh kề của mỗi đỉnh. - Hàng đợi
q- Chứa các đỉnh sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 210;
int n;
int visit[maxN], d[maxN];
vector <int> g[maxN];
int bfs(int s) {
fill_n(d, n + 1, 0);
fill_n(visit, n + 1, false);
queue <int> q;
q.push(s);
visit[s] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
for (auto v : g[u]) {
// Nếu gặp lại đỉnh nguồn, trả ra độ dài chu trình và kết thúc BFS
if (v == s) return d[u] + 1;
if (!visit[v]) {
d[v] = d[u] + 1;
visit[v] = true;
q.push(v);
}
}
}
return 0;
}
int main() {
cin >> n;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j) {
int h;
cin >> h;
if (h) g[i].push_back(j);
}
for (int i = 1; i <= n; ++i) {
int ans = bfs(i);
if (ans) cout << ans << '\n';
else cout << "NO WAY\n";
}
}
¶ Đánh giá
Từ bài toán này, ta có thể áp dụng để tìm chu trình ngắn nhất trong đồ thị có hướng không trọng số bằng cách lấy ra chu trình ngắn nhất trong tất cả các chu trình chứa mỗi đỉnh (nhiều nhất một chu trình từ mỗi bắt đầu từ đỉnh).
Độ phức tạp
Theo đề bài, đồ thị ban đầu được biểu diễn bằng ma trận kề. Nên để tối ưu về mặt thời gian, ta sẽ chuyển đổi cách biểu diễn đồ thị thành danh sách kề.
Theo cách tính toán độ phức tạp thông thường, hàm sẽ mất . Với là số cạnh của đồ thị. Trong trường hợp xấu nhất, mỗi đỉnh đều có cạnh nối tới tất cả các đỉnh của đồ thị (đồng nghĩa, với ), khi đó, số lượng cạnh của đồ thị là .
Vì với mỗi đỉnh của đồ thị, ta phải gọi lại hàm . Nên nhìn chung, độ phức tạp của thuật toán là .
¶ Ứng dụng BFS để tìm đường đi ngắn nhất trong đồ thị có trọng số 0 hoặc 1
¶ Bài toán 7
¶ Đề bài
Cho một đồ thị có hướng đỉnh và cạnh . Tìm số cạnh ít nhất cần phải đảo chiều để tồn tại đường đi từ đỉnh cho đến đỉnh .
Các đỉnh được đánh số từ đến . Đồ thị có thể có nhiều cạnh nối giữa một cặp đỉnh. Và có thể tồn tại cạnh nối từ một đỉnh đến chính nó (đồ thị có thể có khuyên).
¶ Phân tích
Gọi đồ thị ban đầu là .
Ta sẽ thêm các cạnh ngược của mỗi cạnh ban đầu trong đồ thị (nghĩa là, với mỗi cạnh của đồ thị, ta sẽ thêm cạnh vào). Cho các cạnh ngược có trọng số bằng và tất cả các cạnh ban đầu có trọng số bằng . Khi đó, ta sẽ có được đồ thị mới là đồ thị .
Độ dài của đường đi ngắn nhất từ đỉnh cho đến đỉnh trong đồ thị chính là đáp án của bài toán.
- Chứng minh: Trong đồ thị , xét từng cạnh trên một đường đi từ đến . Nếu cạnh đó có trọng số là thì đã tồn tại cạnh đó trên đồ thị ban đầu, còn nếu trọng số là thì cạnh ngược lại của nó tồn tại trong đồ thị . Khi đó ta sẽ phải đảo chiều cạnh đó. Nhận thấy sau khi xét toàn bộ các cạnh, ta sẽ thu được một đường đi từ đến , và số cạnh ta phải đảo chiều chính là số cạnh trong đường đi đó.
Ta sử dụng kĩ thuật 0-1 BFS :
- Nó có tên gọi như vậy vì kĩ thuật 0-1 BFS thường được sử dụng để tìm đường đi ngắn nhất trong đồ thị có trọng số hoặc .
- Khi trọng số của các cạnh bằng hoặc , thuật toán thông thường sẽ trả ra kết quả sai, vì thuật toán thông thường chỉ đúng trong đồ thị có trọng số của các cạnh bằng nhau.
Ta có thể chỉnh sửa một chút từ thuật toán để có được kĩ thuật 0-1 BFS :
- Trong kĩ thuật này, thay vì sử dụng mảng bool để đánh dấu lại các đỉnh đã duyệt, ta sẽ kiểm tra điều kiện khoảng cách ngắn nhất. Nghĩa là, trong quá trình , với mỗi đỉnh kề với , đỉnh chỉ được đẩy vào hàng đợi khi và chỉ khi đường đi đi ngắn nhất từ đỉnh nguồn đến lớn hơn đường đi ngắn nhất từ đỉnh nguồn đến cộng với trọng số cạnh (khoảng cách được giảm bớt khi sử dụng cạnh này) .
- Ta sẽ sử dụng một hàng đợi hai đầu (deque) thay cho hàng đợi (queue) để lưu trữ các đỉnh. Trong quá trình , nếu ta gặp một cạnh có trọng số bằng thì đỉnh sẽ được đẩy vào phía trước của hàng đợi hai đầu. Ngược lại, nếu ta gặp một cạnh có trọng số bằng thì đỉnh sẽ được đẩy vào phía sau của hàng đợi hai đầu.
- Giải thích: Ta push đỉnh kết nối bởi cạnh có trọng số vào đầu deque để giữ cho hàng đợi luôn được sắp xếp theo khoảng cách từ đỉnh nguồn tại mọi thời điểm. Bởi vì, các đỉnh ở gần đầu queue/deque hơn thì nó phải có khoảng cách từ gốc gần hơn, mà đỉnh ta push vào đầu có khoảng cách bằng chính khoảng cách đỉnh vừa pop ra, nên deque lúc này thỏa mãn tính chất của queue trong .
- Từ tính chất trên, ta có nhận xét sau: Kĩ thuật 0-1 BFS vẫn đúng cho trường hợp đồ thị có trọng số cạnh là hoặc .
Cách tiếp cận của kĩ thuật 0-1 BFS khá giống với thuật toán + Dijkstra.
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
inf = 1000000000. - Hằng số
maxN = 100007. - Mảng
d[]- Mảng lưu lại khoảng cách ngắn nhất từ đỉnh nguồn đến mỗi đỉnh. - Vector
g[]- Danh sách cạnh kề của mỗi đỉnh. - Hàng đợi hai đầu
q- Chứa các đỉnh sẽ được duyệt theo thứ tự.
#include <bits/stdc++.h>
using namespace std;
const int inf = 1e9;
const int maxN = 1e5 + 7;
int n, m;
int d[maxN];
vector < pair <int, int> > g[maxN];
void bfs(int s) {
fill_n(d, n + 1, inf);
deque <int> q;
q.push_back(s);
d[s] = 0;
while (!q.empty()) {
int u = q.front();
q.pop_front();
if (u == n) return;
for (auto edge : g[u]) {
int v = edge.second;
int w = edge.first;
if (d[v] > d[u] + w) {
d[v] = d[u] + w;
if (w) q.push_back(v);
else q.push_front(v);
}
}
}
d[n] = -1;
}
int main() {
cin >> n >> m;
while (m--) {
int u, v;
cin >> u >> v;
g[u].push_back({0, v});
g[v].push_back({1, u});
}
bfs(1);
cout << d[n];
}
¶ Đánh giá
Ta cũng có thể giải quyết bài toán này bằng thuật toán với độ phức tạp .
Trong khi sử dụng , độ phức tạp sẽ là . Nó tuyến tính và hiệu quả hơn thuật toán .
¶ Bài tập áp dụng
Three States - 590C Codeforces
Olya and Energy Drinks - 877D Codeforces
Minimum Cost to Make at Least One Valid Path in a Grid
¶ Ứng dụng BFS để kiểm tra đồ thị hai phía (Bipartite graph)
¶ Định nghĩa
Trong Lý thuyết đồ thị, đồ thị hai phía (đồ thị lưỡng phân hay đồ thị hai phần - Bipartite graph) là một đồ thị đặc biệt, trong đó tập hợp các đỉnh của đồ thị có thể được chia làm hai tập hợp không giao nhau thỏa mãn điều kiện không có cạnh nối hai đỉnh bất kỳ thuộc cùng một tập.
Có rất nhiều tình huống thực tế có thể mô phỏng bằng đồ thị hai phía:
- Ví dụ: Muốn biểu diễn mối quan hệ giữa một nhóm học sinh và một nhóm các trường học, ta có thể xây dựng một đồ thị với mỗi một học sinh và mỗi trường học là một đỉnh. Giữa một người và một trường sẽ có một cạnh nếu như đã hoặc đang đi học ở trường . Kiểu đồ thị này sẽ là một đồ thị hai phần, với một nhóm đỉnh là người và nhóm kia là trường; sẽ không có cạnh nối giữa hai người hoặc giữa hai trường.
Một tính chất thú vị của đồ thị hai phía là ta có thể tô màu các đỉnh đồ thị với hai màu sao cho không có hai đỉnh nào cùng màu kề nhau.
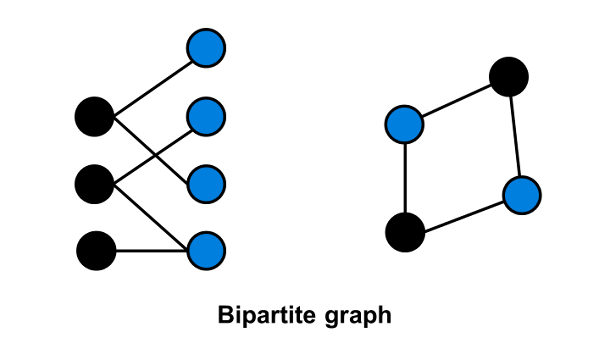
Bạn có thể tìm hiểu thêm về đồ thị hai phía tại đây.
¶ Bài toán 8
¶ Đề bài
Cho một đồ thị vô hướng liên thông gồm đỉnh . Các đỉnh được đánh số từ đến . Và không tồn tại cạnh nối từ một đỉnh đến chính nó (đồ thị không có khuyên).
Bạn hãy kiểm tra xem đồ thị có thể được tô bằng màu hay không. Nghĩa là ta có thể gán màu (từ một bảng gồm màu) cho mỗi đỉnh của đồ thị theo cách sao cho không có đỉnh nào kề cạnh nhau có cùng màu.
¶ Phân tích
Theo đề bài, ta phải kiểm tra xem đồ thị có thể được tô bằng màu sao cho không có đỉnh nào kề cạnh nhau có cùng màu hay không. Điều đó tương đương với việc kiểm tra xem đồ thị đã cho có phải là đồ thị hai phía hay không.
Ta có thể dùng thuật toán để kiểm tra xem một đồ thị có phải đồ thị hai phía, bằng cách tìm kiếm từ một đỉnh bất kì và tô màu cho các đỉnh được xem xét. Nghĩa là, ta tô màu đen cho đỉnh gốc, tô màu xanh cho tất cả các đỉnh kề đỉnh gốc, tô màu đen cho tất cả các đỉnh kề với một đỉnh kề đỉnh gốc, và tiếp tục như vậy. Nếu ở một bước nào đó, hai đỉnh kề nhau có cùng màu, thì đồ thị không phải là hai phía. Nếu quá trình tìm kiếm kết thúc mà điều này không xảy ra thì đồ thị là hai phía.
Thuật toán này đúng với đồ thị liên thông. Với đồ thị gồm nhiều thành phần liên thông thì ta phải duyệt từng thành phần liên thông một như thuật toán tìm số thành phần liên thông và áp dụng thủ tục tương ứng.
¶ Mô tả
- Ví dụ mô tả đồ thị không phải là đồ thị hai phía:
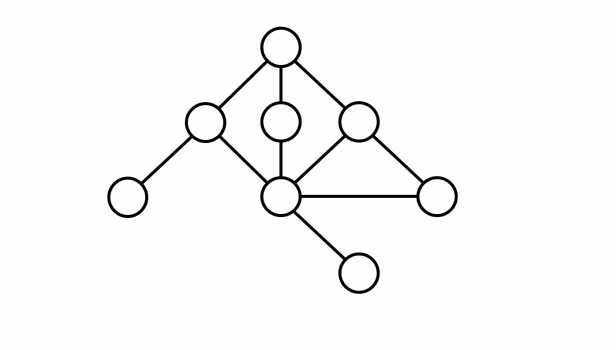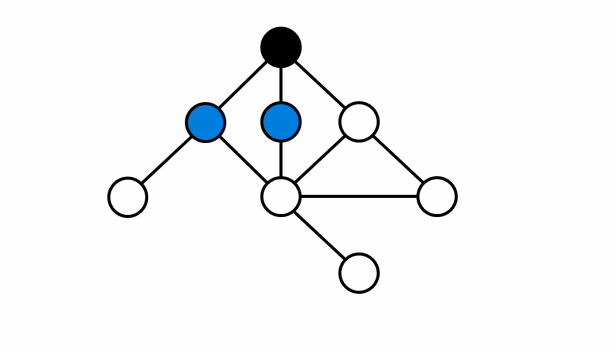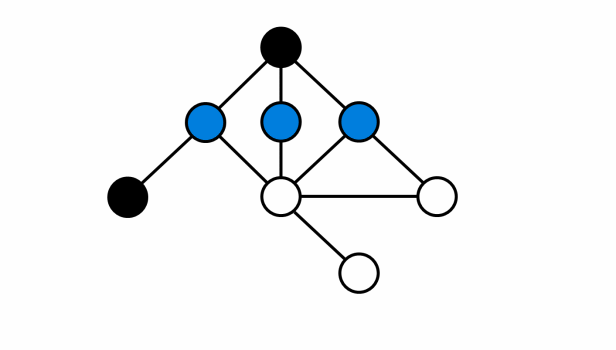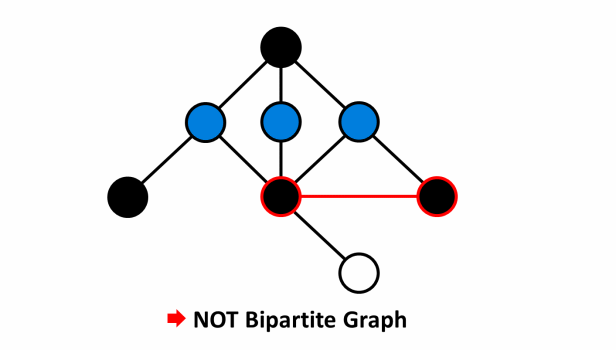
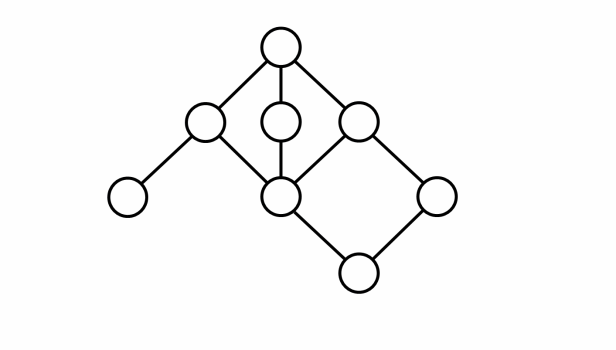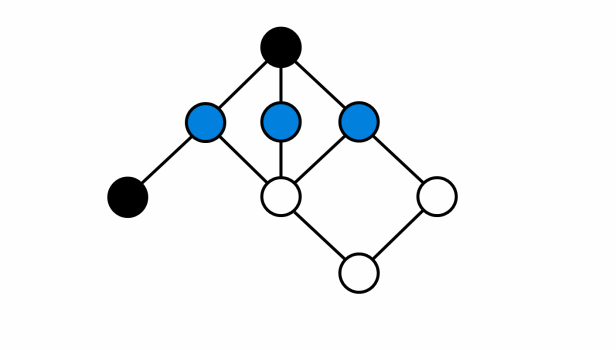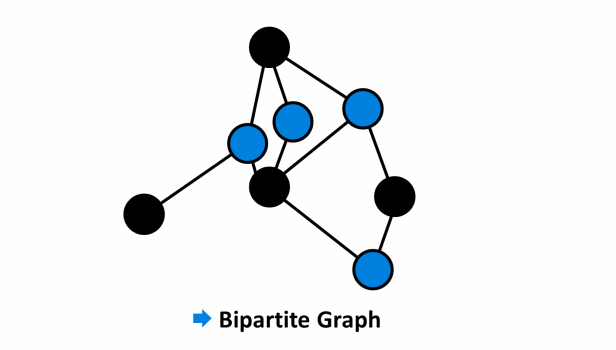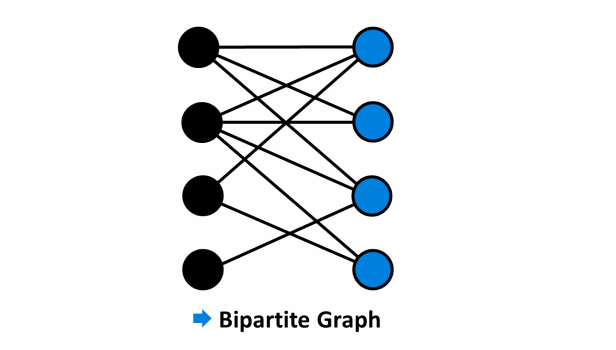
- Ví dụ mô tả đồ thị hai phía:
¶ Thuật toán
Để tô màu đồ thị, ta sẽ sử dụng mảng để lưu trạng thái của mỗi đỉnh. Có trạng thái:
- Trạng thái -1: Đỉnh vẫn chưa được tô màu (đỉnh chưa được duyệt).
- Trạng thái 0: Đỉnh được tô màu đen.
- Trạng thái 1: Đỉnh được tô màu xanh.
Ban đầu, tất cả các đỉnh của đồ thị đều ở trạng thái -1.
Ta sử dụng để tô màu đồ thị:
- Bắt đầu từ một đỉnh bất kỳ và tô màu đen cho đỉnh đó.
- Với mỗi đỉnh kề với đỉnh đang xét , nếu đỉnh chưa được duyệt, ta sẽ tô màu ngược với màu của (nếu là màu xanh, ta sẽ tô màu đen và ngược lại).
- Nếu đã được thăm trước đó và có cùng màu với , ta sẽ dừng thuật toán và kết luận đồ thị không phải đồ thị hai phía.
Cuối cùng, nếu ta có thể tô màu tất cả các đỉnh mà không vi phạm quy tắc tô màu, ta có thể kết luận đồ thị là hai phía.
¶ Cài đặt
Cấu trúc dữ liệu:
- Hằng số
maxN = 210. - Mảng
color[]- Mảng lưu trạng thái tô màu của mỗi đỉnh. - Vector
g[]- Danh sách cạnh kề của mỗi đỉnh. - Hàng đợi
q- Chứa các đỉnh sẽ được duyệt theo thứ tự ưu tiên chiều rộng.
#include <bits/stdc++.h>
using namespace std;
const int maxN = 210;
int n, l;
int color[maxN];
vector <int> g[maxN];
bool checkBipartiteGraph() {
fill_n(color, n + 1, -1);
queue <int> q;
q.push(0);
color[0] = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
for (auto v : g[u]) {
if (color[v] == color[u]) return false;
if (color[v] == -1) {
color[v] = !color[u];
q.push(v);
}
}
}
return true;
}
int main() {
while (cin >> n){
if (!n) return 0;
cin >> l;
while (l--) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
if (!checkBipartiteGraph()) cout << "NOT ";
cout << "BICOLORABLE.\n";
for (int i = 0; i < n; ++i) g[i].clear();
}
}
¶ Đánh giá
Ta cũng có thể sử dụng thuật toán tìm kiếm theo chiều sâu (Depth First Search – DFS) để kiểm tra đồ thị hai phía.
Độ phức tạp
Độ phức tạp của thuật toán là . Với là số lượng bộ test.