¶ Bài toán Luồng cực đại trên mạng
Tác giả:
- Nguyễn Đức Kiên, Trường Đại học Công nghệ, ĐHQGHN.
Reviewer:
- Phạm Công Minh - THPT chuyên Khoa học Tự Nhiên, ĐHQGHN
- Đặng Đoàn Đức Trung - UT Austin
- Nguyễn Minh Nhật - Trường THPT chuyên Khoa học Tự nhiên, ĐHQGHN
Luồng cực đại (Maximum Flow) và Lát cắt cực tiểu/hẹp nhất (Minimum Cut) là những bài toán quan trọng trong lớp các bài toán về đồ thị. Bài viết sau đây sẽ giới thiệu một vài nội dung cơ bản về bài toán luồng cực đại và các thuật toán liên quan.
¶ Một số khái niệm sử dụng trong bài viết
Để hiểu hơn về phần này, bạn đọc nên có sẵn những kiến thức cơ bản về đồ thị, cũng như biểu diễn và duyệt (BFS, DFS, ...) chúng.
Bài viết sẽ không nêu lại các khái niệm cơ bản về đồ thị.
- Ký hiệu đồ thị có : Đồ thị tập các đỉnh là và tập các cạnh là
- Cạnh đi vào đỉnh : Các cạnh có dạng , với là đỉnh bất kỳ của đồ thị.
- Cạnh đi ra khỏi đỉnh : Các cạnh có dạng , với là đỉnh bất kỳ của đồ thị.
- Đường đi đơn từ tới : Dãy các đỉnh sao cho giữa hai đỉnh liên tiếp trong dãy tồn tại một cạnh nối chúng theo đúng chiều như trên.
¶ Bài toán Luồng cực đại
¶ Các định nghĩa
Có rất nhiều hình ảnh thực tế để miêu tả một mạng và luồng trên mạng đó, như một mạng điện, một mạng kết nối dữ liệu giữa các máy, hay phổ biến hơn là một hệ thông ống nước.
Một đồ thị được gọi là mạng (network) nếu nó là đồ thị có hướng, trong đó:
- Tồn tại một đỉnh không có cạnh đi vào, gọi là đỉnh phát/nguồn (source)
- Tồn tại một đỉnh không có cạnh đi ra, gọi là đỉnh thu/đích (sink)
- Mỗi cạnh được gán một trọng số , gọi là khả năng thông qua/dung lượng (capacity) của cạnh.

Một mạng hợp lệ. Đỉnh phát và đỉnh thu được đánh dấu bằng hai màu khác.
Một luồng (flow) trên mạng là một phép gán cho mỗi cạnh một số thực thoả mãn:
- Luồng trên mỗi cạnh có giá trị không vượt quá khả năng thông qua của cạnh đó:
- Với mọi đỉnh không trùng với đỉnh phát và đỉnh thu , tổng luồng trên các cạnh đi vào bằng tổng luồng trên các cạnh đi ra . Tính chất này tương đối giống với định luật I Kirchoff của dòng điện.
- Giá trị được gọi là luồng trên cạnh
- Giá trị của luồng là tổng luồng trên các cạnh đi ra khỏi đỉnh phát, cũng chính là tổng luồng trên các cạnh đi vào đỉnh thu.

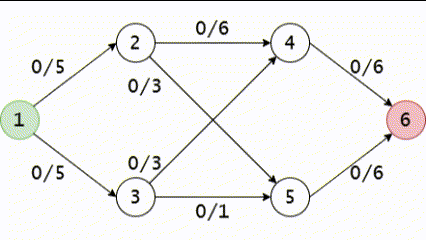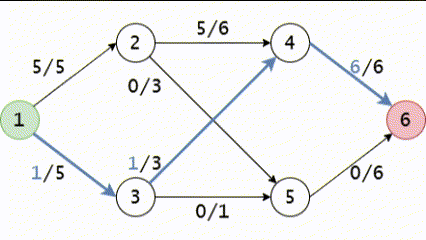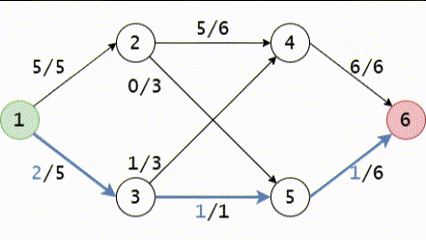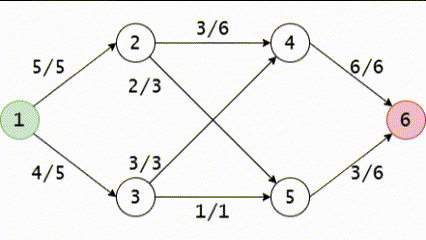
Một luồng hợp lệ. Giá trị f/c trên cạnh biểu diễn luồng/khả năng thông qua.
Một lát cắt (cut) trên mạng là một cách chia các đỉnh trên đồ thị mạng thành hai tập hợp sao cho .
Tổng các giá trị khả năng thông qua trên các cạnh nối giữa một đỉnh thuộc và một đỉnh thuộc được gọi là khả năng thông qua (cut value) của lát cắt

Một lát cắt hợp lệ với hai tập và . Mỗi tập con của lát cắt được đánh dấu bằng một màu khác nhau. Lát cắt này có khả năng thông qua là .
Định lý: Trên cùng một mạng, tất cả mọi luồng đều có giá trị không lớn hơn khả năng thông qua của một lát cắt bất kỳ.
Chứng minh
Xét luồng có giá trị và lát cắt trên một mạng bất kỳ. Ta có:
(đpcm)
Nếu ta hiểu mạng như một hệ thống ống nước, nó sẽ như sau:
- Nước chảy qua một hệ thống các ống, từ nguồn nước (đỉnh phát) đến bồn chứa (đỉnh thu).
- Mỗi ống có một giới hạn nhất định. Lượng nước chảy qua ống này không thể vượt quá giới hạn này.
- Hiển nhiên, tại mỗi điểm nút (trừ điểm đầu và điểm cuối), có bao nhiêu nước đến thì sẽ có bấy nhiêu nước chảy đi. Nước không tự sinh ra và mất đi, chúng chỉ chảy từ điểm này sang điểm khác.
- Và tất nhiên tổng lượng nước xuất hiện trong mạng sẽ là lượng nước ta cấp cho nguồn. Bể chứa cũng sẽ thu được từng đó nước.
- Còn một lát cắt là một cách bỏ đi các ống sao cho nước không thể chảy từ nguồn đến bể nữa bằng bất kỳ cách nào.
¶ Bài toán
Đề bài: Cho mạng với đỉnh và cạnh có đỉnh phát là , đỉnh thu là (). Hãy tìm một luồng trong mạng sao cho giá trị của nó là lớn nhất.
Luồng này gọi là luồng cực đại trên mạng .
Đề bài VNOI: NKFLOW
¶ Phương pháp Ford-Fulkerson. Thuật toán Edmonds-Karp.
Đôi lời về lịch sử thuật toán
Năm 1956, L. R. Ford Jr. và D. R. Fulkerson đề xuất một phương pháp để tìm ra luồng cực đại trên mạng. Tuy nhiên, phương pháp này không chỉ rõ việc tìm đường tăng luồng như thế nào. Đến năm 1972, Jack Edmonds and Richard Karp đã hoàn thiện phương pháp trên bằng cách sử dụng thuật BFS để tìm đường tăng luồng.
Nhiều tài liệu mà chúng ta đang dùng có sử dụng cụm từ "thuật toán Ford-Fulkerson" để gọi thuật tìm luồng cực đại hoàn chỉnh, và biến "thuật toán Edmonds-Karp" thành một thuật xa lạ kì quặc nào đó. Điều này có lẽ cũng ... không hẳn là sai. Bài viết này sẽ sử dụng tên Edmonds-Karp cho thuật toán, và chỉ gọi là "phương pháp Ford-Fulkerson" thôi. Bạn đọc muốn hiểu theo cách nào cũng được.
¶ Các khái niệm
Giả sử tại một thời điểm, ta đã có một luồng trên đồ thị, với giá trị luồng trên cạnh là .
Với mọi cạnh , ta định nghĩa thêm giá trị . Về mặt ý nghĩa, việc định nghĩa này cho ta biết luồng hiện tại trên cạnh này có thể giảm đi một lượng bao nhiêu.
Lưu ý rằng ta không định nghĩa , giá trị này vẫn được mặc định bằng .
Định nghĩa luồng thặng dư (residual flow) trên một cạnh tại một thời điểm là hiệu của khả năng thông qua và giá trị luồng hiện tại trên cạnh đó:
Giá trị này cũng áp dụng cho cả các cạnh đảo (cạnh có luồng âm), khi đó
.
Ta có thể hiểu rằng giá trị luồng thặng dư cho biết còn có thể thêm vào luồng này một lượng bao nhiêu.
Với các giá trị này, ta có thể xây dựng một đồ thị thặng dư/đồ thị tăng luồng (residual network). Ứng với mỗi cạnh trên mạng ban đầu, trên đồ thị thặng dư sẽ có hai cạnh:
- Cạnh , với trọng số là . Mỗi cạnh loại này cho ta biết có thể tăng luồng trên mạng ban đầu bao nhiêu.
- Cạnh , với trọng số là . Mỗi cạnh loại này cho ta biết có thể giảm luồng trên mạng ban đầu bao nhiêu.
Một đường tăng luồng (augmenting path) là một đường đi đơn trên đồ thị thặng dư. Đối chiếu lại với đồ thị gốc, đó sẽ là một đường đi đơn (có thể đi ngược chiều cạnh) qua những cạnh có . Trên đường này, chúng ta có thể thực hiện tăng giá trị của luồng trên mỗi cạnh.

Đường màu xanh là một đường tăng luồng trên đồ thị thặng dư trên. Các cạnh đứt chính là các cạnh "ngược" so với mạng ban đầu; chúng có giá trị âm.

Đem đối chiếu đồ thị thặng dư trên về đồ thị gốc, ta được đường tăng luồng như hình trên. Trong hình dưới, giá trị của luồng () trên các cạnh thuộc đường tăng luồng đã được tăng đơn vị so với đồ thị thặng dư bên trên.
Việc xây dựng cả một đồ thị thặng dư sau từng bước rất tốn thời gian và bộ nhớ. Vì vậy, trong phương pháp Ford-Fulkerson chúng ta sẽ chỉ sử dụng đồ thị gốc, và thực hiện tìm đường tăng luồng trực tiếp trên đồ thị này.
Còn nếu bạn muốn hiểu theo kiểu "ống nước" thì đường tăng luồng có thể coi như một đường nước chảy từ nguồn đến bể chứa. Đối với các "ống đi ngược" như "ống" trên hình, ta hiểu đây là một cách phân phối lại nước: thêm đơn vị nước vào nút sẽ dẫn đến việc phải bớt đơn vị từ ống để đảm bảo đoạn sau vẫn đủ nước; ở đầu phần nước thay vì chảy vào ống này đi ra đầu thì nó sẽ đưa phần nước này sang ống .
¶ Thuật toán
Đầu tiên ta gán giá trị mọi luồng trên tất cả mọi cạnh thành .
Ta đi tìm một đường tăng luồng có thể có trên đồ thị. Nhắc lại rằng, đường tăng luồng chỉ chứa các cạnh (kể cả "cạnh" ngược) có , hay .
Trên đường này, với mỗi cạnh , ta tăng giá trị của luồng trên cạnh này (tức ) lên đơn vị, với là giá trị nhỏ nhất trên đường tăng luồng vừa tìm được. Đồng thời, ta cũng phải giảm đi để luôn có .
Một cách dễ hiểu hơn thì tại bước này, ta tăng giá trị của luồng trên đường vừa tìm được đến mức tối đa có thể.
Ta lặp đi lặp lại việc tăng luồng cho đến khi nào không thể tìm được đường tăng luồng nữa thì thôi. Khi đó, giá trị của luồng trong cả mạng chính là luồng cực đại mà ta cần tìm.
Hình GIF trên mô tả phương pháp Ford-Fulkerson trên mạng ta vừa lấy ví dụ trong bài viết này. Chú ý rằng có một bước, chúng ta đã phải sử dụng cạnh ngược.
Để tìm đường tăng luồng, ta chỉ phải tìm một đường để đi từ tới , qua các cạnh có . Đây chỉ là một bài toán duyệt đồ thị đơn giản, ta có thể thử áp dụng DFS, BFS, ... để duyệt.
Hai thuật BFS và DFS có độ phức tạp giống nhau, nhưng trên thực tế BFS chạy nhanh hơn DFS khi đi tìm đường tăng luồng. Thuật Edmonds-Karp sử dụng BFS.
¶ Tính đúng đắn
Định lý: Phương pháp Ford-Fulkerson cho kết quả là luồng cực đại.
Chứng minh
Giả sử thuật toán cho một luồng có giá trị là .
Tại bước cuối cùng của thuật toán, chúng ta không thể tìm được một đường tăng luồng nào từ tới nữa. Gọi là tập tất cả các đỉnh trên đồ thị có thể đi tới từ theo một đường tăng luồng, và là tập các đỉnh còn lại. Khi đó là một lát cắt trên mạng.
Ta chứng minh . Nhắc lại rằng là khả năng thông qua của lát cắt .
Gọi là một cạnh bất kỳ nối từ sang , với . Cạnh phải thoả mãn , nếu không sẽ tồn tại một đường tăng luồng đi từ sang tập , trái với giả thiết.
Lại gọi là một cạnh bất kỳ nối từ sang , với . Nếu , sẽ tồn tại một đường tăng luồng đi qua cạnh ngược do , trái với giả thiết không tồn tại đường đi từ sang .
Lấy tổng tất cả các đẳng thức và với mọi cặp đỉnh thoả mãn một trong hai trường hợp trên, ta được:
Nhưng theo định lý về luồng và lát cắt đã trình bày ở trên ta có nên đây là luồng cực đại. (đpcm)
Hệ quả:
- Khả năng thông qua của lát cắt hẹp nhất trên một mạng bằng giá trị của luồng cực đại trên mạng đó. Lát cắt hẹp nhất (mincut) là lát cắt có khả năng thông qua nhỏ nhất trong số mọi lát cắt thuộc mạng.
- Nếu mọi giá trị trên luồng đều là số nguyên thì giá trị luồng cực đại cũng là số nguyên.
¶ Cài đặt
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1001;
int n, m, s, t;
vector <int> adj[MAXN]; //đồ thị lưu kiểu danh sách kề
int c[MAXN][MAXN], f[MAXN][MAXN], trace[MAXN], maxFlow;
//BFS để tìm đường tăng luồng
void bfs()
{
fill(trace, trace + n + 1, 0);
trace[s] = -1;
queue <int> bfsQueue;
bfsQueue.push(s);
while (!bfsQueue.empty())
{
int u = bfsQueue.front();
bfsQueue.pop();
for (auto v : adj[u])
{
//Không dẫm lại đường cũ theo đúng luật BFS
if (trace[v]) continue;
//Không đi qua cạnh có r(u, v) = c(u, v) - f(u, v) = 0
if (f[u][v] - c[u][v] == 0) continue;
//Các công việc còn lại của BFS
trace[v] = u;
bfsQueue.push(v);
}
}
}
//Hàm tăng luồng
void incFlow()
{
//Đi ngược theo đường tăng luồng để tìm giá trị delta = c - f tốt nhất
int delta = INT_MAX;
int v = t;
while (v != s)
{
int u = trace[v];
delta = min(delta, c[u][v] - f[u][v]);
v = u;
}
maxFlow += delta;
//Đi ngược theo đường tăng luồng một lần nữa để cập nhật giá trị f
v = t;
while (v != s)
{
int u = trace[v];
f[u][v] += delta;
f[v][u] -= delta;
v = u;
}
}
int main()
{
cin >> n >> m >> s >> t;
for (int u, v, i = 1; i <= m; i ++)
{
cin >> u >> v;
cin >> c[u][v];
adj[u].push_back(v);
adj[v].push_back(u); //lưu thêm cạnh ngược để có thể chạy qua nó khi tăng luồng
}
maxFlow = 0;
//Tăng luồng đến khi không tăng được nữa
do
{
bfs();
if (trace[t]) incFlow();
} while (trace[t]);
cout << maxFlow;
}
¶ Độ phức tạp
Trong bài toán chúng ta xét, tất cả các khả năng thông qua của các cạnh đều là số nguyên. Do đó, mỗi bước tăng luồng đều làm tăng giá trị của luồng lên ít nhất đơn vị. Khi sử dụng thuật BFS hoặc DFS để tìm đường tăng luồng, độ phức tạp sẽ vào cỡ . Do đó, độ phức tạp của phương pháp Ford-Fulkerson sẽ là , với là giá trị của luồng cực đại trên mạng. Đây không phải là một độ phức tạp với thời gian đa thức trên kích thước đồ thị.
Với thuật toán Edmonds-Karp, khi sử dụng BFS, sau lần tìm đường tăng luồng, chúng ta sẽ tìm được kết quả. Độ phức tạp của thuật toán này là .
Bạn có thể tham khảo chứng minh độ phức tạp này tại đây.
Khi thực hiện giải thuật Edmonds-Karp, các đánh giá ban đầu về độ phức tạp có thể sai lệch nhiều so với thực tế. Mặc dù độ phức tạp của thuật toán là tương đối lớn trong trường hợp tệ nhất, nó vẫn hoạt động hiệu quả trong hầu hết các trường hợp.
¶ Thuật toán Dinic
Như đã nói ở trên, tuy đánh giá về độ phức tạp của thuật Edmonds-Karp không hề đẹp, nó vẫn chạy đủ nhanh trong thực tế. Tất nhiên, vẫn có những trường hợp thuật này chạy chưa được ổn lắm, điển hình là khi mạng có rất nhiều cạnh, ví dụ có dạng của đồ thị đầy đủ với cạnh thì độ phức tạp của thuật toán sẽ là , rất khủng khiếp. Thuật toán Dinic sẽ làm giảm độ phức tạp của thuật đi một chút.
Thuật toán này được Yefim A. Dinitz (nhiều tài liệu để tên là E. A. Dinic) đề xuất năm 1970. Nó được chứng minh là có độ phức tạp , tốt hơn thuật toán Edmonds-Karp.
Thuật toán Dinic sử dụng nhiều ý tưởng của phương pháp Ford-Fulkerson để tìm đường tăng luồng. Để đọc và hiểu được phần dưới đây, bạn nên có kiến thức về phương pháp này trước.
¶ Các khái niệm
- Thuật toán Dinic vẫn sử dụng khái niệm đồ thị thặng dư giống như trong phương pháp Ford-Fulkerson. Nhắc lại, đồ thị thặng dư là đồ thị mà ứng với mỗi cạnh sẽ có hai cạnh, một cạnh có trọng số và một cạnh có trọng số .
- Một luồng cản (blocked flow) là một tập các cạnh trên đồ thị có dạng giống như luồng trên mạng sao cho mọi đường đi từ đến đều chứa ít nhất một cạnh thuộc tập này.
- Gọi là mức/cấp (level) của đỉnh - đường đi ngắn nhất (tính bằng số cạnh) để đi từ đến trên đồ thị thặng dư. Định nghĩa đồ thị phân cấp (layered network) của đồ thị ban đầu là đồ thị chỉ chứa các cạnh có trọng số dương thoả mãn , tức là các cạnh tham gia tạo thành đường đi ngắn nhất đến tất cả các đỉnh.

Đồ thị phân cấp (tất cả các đường có màu) và luồng cản (xanh lam) của đồ thị thặng dư
¶ Thuật toán
Ta dựng đồ thị phân cấp của đồ thị thặng dư. Trên đồ thị này, ta tìm một luồng cản rồi tăng luồng ở tất cả các cạnh trên luồng cản này càng nhiều càng tốt. Nói cách khác, đây là phương pháp Ford-Fulkerson với các đường tăng luồng là các đường cản trong luồng cản. Lặp lại quá trình trên cho tới khi ta không thể tìm được đường đi từ tới trên đồ thị phân cấp nữa, hay không xác định.
Để tìm luồng cản, ta sử dụng DFS để tìm từng đường cản một. Mỗi đường cản là một đường đi có trọng số dương từ tới trên đồ thị phân cấp. Đây là lý do thuật Dinic được gọi là "dùng cả BFS và DFS để tìm luồng".
Để tối ưu việc cài đặt, ta có thể:
- Không dựng đồ thị thặng dư và đồ thị phân cấp. Cũng như thuật toán Edmonds-Karp, ta hoàn toàn có thể sử dụng thêm các "cạnh" ngược với giá trị luồng âm để biểu diễn các cạnh ngược trong đồ thị thặng dư. Việc sử dụng đồ thị phân cấp thì chỉ là đánh các nhãn cho các đỉnh của đồ thị, rồi kiểm tra và để biết cạnh (kể cả ngược) có thuộc đồ thị phân cấp không.
- Tại mỗi đỉnh, chỉ DFS từ cạnh cuối cùng được xét trong lần tìm đường cản trước đó với cùng một bộ (hay cùng một đồ thị phân cấp) (xem code để hiểu phần này hơn). Việc tiếp tục sử dụng một cạnh nào đó của các đường trước đó để tăng luồng là vô nghĩa, vì trong những lần tìm trước đó, ta đã khẳng định là chúng không thể tạo ra đường cản mới rồi. Khi không tìm được bất kỳ đường cản nào nữa, luồng cản hiện tại coi như đã xong. Ta tăng luồng và đánh lại cho các đỉnh.

Hình GIF trên mô tả thuật toán Dinic. Tất cả các cạnh có màu đều là các cạnh nằm trên đồ thị phân cấp. Các cạnh màu xanh và đỏ là các cạnh nằm trên luồng cản tìm được sau mỗi bước.
¶ Tính đúng đắn
Định lý: Thuật toán Dinic cho kết quả là luồng cực đại
Chứng minh
Thuật toán Dinic dừng khi nó không thể tìm một đường cản trên đồ thị phân cấp. Khi đó, không tồn tại một đường đi từ đến trên đồ thị này, suy ra trong đồ thị thặng dư cũng không tồn tại một đường như vậy mà không phải đi qua những cạnh có trọng số bằng - những cạnh đầy. Do vậy luồng tìm được là cực đại (đpcm).
¶ Cài đặt
Trong bước DFS, để lập trình đơn giản hơn một chút, ta sẽ kết hợp DFS và tăng luồng. Mỗi lần đi tìm đường cản, ta có thể kết hợp lưu lại giá trị nhỏ nhất trên đường này luôn, và khi đường này đến được , ta thực hiện tăng luồng trên những cạnh đã xét.
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1001;
const int INF = 1e9 + 7;
int n, m, s, t;
vector <int> adj[MAXN];
int c[MAXN][MAXN], f[MAXN][MAXN], d[MAXN], maxFlow;
//chỉ số của cạnh cuối cùng được xét trong danh sách kề
int curVertexId[MAXN];
//BFS để tìm mức (d) của mỗi đỉnh
void bfs()
{
fill(d, d + n + 1, INF);
d[s] = 0;
queue <int> bfsQueue;
bfsQueue.push(s);
while (!bfsQueue.empty())
{
int u = bfsQueue.front();
bfsQueue.pop();
for (auto v : adj[u])
{
if (d[v] != INF) continue;
if (f[u][v] - c[u][v] == 0) continue; //chỉ xét cạnh dương
d[v] = d[u] + 1;
bfsQueue.push(v);
}
}
}
//DFS tìm luồng cản.
//curDelta: giá trị delta tốt nhất hiện có trên đường từ s tới u
//Hàm trả về giá trị delta tốt nhất sau khi tìm xong đường cản.
int dfs(int u, int curDelta)
{
if (curDelta == 0) return 0;
if (u == t) return curDelta;
//Chỉ xét từ cạnh cuối cùng
for (; curVertexId[u] < adj[u].size(); curVertexId[u] ++)
{
int v = adj[u][curVertexId[u]];
//Chỉ xét cạnh thuộc đồ thị phân cấp
if (d[v] != d[u] + 1) continue;
if (f[u][v] == c[u][v]) continue;
//Thực hiện tăng luồng
int delta = dfs(v, min(c[u][v] - f[u][v], curDelta));
if (delta == 0) continue;
f[u][v] += delta;
f[v][u] -= delta;
return delta;
}
return 0;
}
int32_t main()
{
cin >> n >> m >> s >> t;
for (int u, v, i = 1; i <= m; i ++)
{
cin >> u >> v;
cin >> c[u][v];
adj[u].push_back(v);
adj[v].push_back(u);
}
maxFlow = 0;
while (true)
{
bfs();
if (d[t] == INF) break;
for (int i = 1; i <= n; i ++) curVertexId[i] = 0;
while (int delta = dfs(s, INF))
maxFlow += delta;
}
cout << maxFlow;
}
¶ Độ phức tạp
Định lý: Thuật toán Dinic có độ phức tạp là
Chứng minh
Gọi là mức của đỉnh sau khi thực hiện lần BFS và gán nhãn . Ta chứng minh hai bổ đề sau:
Bổ đề 1:
Xét vòng BFS thứ , đang xét đến đỉnh . Xét đồ thị là đồ thị thặng dư ở lượt BFS thứ . Dễ thấy luôn bao gồm một số cạnh trong cùng với một số cạnh ngược trong .
Tại vòng thứ , trường hợp đường đi từ đến không đi qua cạnh ngược, hiển nhiên đường đi này phải xuất hiện trên , cho nên .
Trường hợp đường đi này chứa cạnh ngược, giả sử cạnh đầu tiên như vậy là cạnh . Theo trường hợp đầu, (1). Ở vòng thứ , đường này vẫn còn đi được, do đó (2). Nhưng tại vòng , cạnh này trở thành cạnh ngược, cho nên (3). Từ (1), (2), (3) suy ra .
Tóm lại, trong cả hai trường hợp ta đều có . Bổ đề được chứng minh.
Bổ đề 2:
Theo bổ đề 1, . Giả sử . Vì chỉ chứa các cạnh xuôi và cạnh ngược trong nên phải tồn tại một đường đi từ tới , trái với giả thiết một luồng cản được tạo ra. Bổ đề được chứng minh.
Theo bổ đề 2, tăng nghiêm ngặt sau mỗi lần BFS, nhưng không vượt quá . Do vậy, thuật toán Dinic sẽ BFS tối đa lần.
Chi phí cho một lần tìm luồng cản là , với dùng cho DFS trên đồ thị phân cấp, và cho việc duyệt tất cả các cạnh để tìm đường DFS. Lưu ý do duyệt từ cạnh cuối cùng được DFS, đoạn này chỉ mất thay vì .
Tổng kết hai phần lại, chúng ta có độ phức tạp thuật toán Dinic là . (đpcm)
¶ Bài toán ví dụ
Đề bài VNOI: FLOW1
Tóm tắt đề bài: Có học sinh đến từ hai trường SP, TH và bài toán. Mỗi học sinh có thể giải tốt một số bài toán cho trước. Cần chọn bài toán sao cho:
- Với mỗi bài toán, mỗi trường có đúng một học sinh giải được bài đó
- Không có học sinh nào làm hai bài toán
- Không có hai học sinh nào cùng trường làm cùng một bài toán.
Phân tích
Theo như đề bài, ta cần chọn ra bộ ba phân biệt gồm học sinh trường SP, học sinh trường TH, và một bài toán. Việc này có thể giúp chúng ta liên tưởng đến luồng cực đại, bằng cách đảm bảo rằng ba phần trên sẽ liên tiếp được chọn, và chỉ tồn tại đúng bộ như vậy. Chúng ta xây dựng mạng sao cho đỉnh đầu tiên đại diện cho học sinh trường SP, và đỉnh khác đại diện cho học sinh trường TH. Đối với các bài toán, chúng ta thêm các cạnh nối chúng với một học sinh khi học sinh đó giải được bài toán này. Khả năng thông qua của các cạnh này là , do mỗi học sinh chỉ được giải bài toán. Tuy nhiên, như vậy vẫn chưa giải quyết được tình trạng một bài toán bị giải nhiều lần. Vì vậy, ta lại tách mỗi bài toán làm đỉnh nối với nhau bằng một cạnh với khả năng thông qua là . Lúc này, ta sẽ có một đường đi thống nhất từ một học sinh trường SP, qua một bài toán, đến một học sinh trường TH, và cũng đảm bảo rằng bài toán chỉ được chọn một lần.
Ta cũng thêm một đỉnh phát nối với tập các học sinh SP, một đỉnh thu nối với tập các học sinh TH, tất cả các cạnh nối này đều có trọng số bằng .
Mạng của chúng ta sẽ có dạng như thế này

Để truy vết, ta thực hiện tìm đường trên luồng mà ta đã tìm được, cũng chính là các cạnh có giá trị luồng đạt cực đại.
Phần cài đặt chi tiết thuật toán trên sẽ dành cho bạn đọc.
¶ Một số chú ý
- Khi giải các bài toán về luồng hoặc lát cắt, loại bài liên quan đến mạng đơn vị (mạng có các khả năng thông qua trên các cạnh là ) khá phổ biến. Trên những mạng này, khi tìm thành công luồng cực đại, luồng các cạnh sẽ chỉ ở một trong hai trạng thái: đầy () hoặc rỗng (); còn luồng cực đại sẽ có dạng một số đường đi không giao nhau.
- Khi mạng đơn vị có dạng đồ thị hai phía (đồ thị có thể chia các đỉnh thành tập hợp sao cho không có hai đỉnh nào cùng một tập hợp có cạnh nối đến nhau) cùng với đỉnh nguồn và đỉnh đích, bài toán trở thành dạng cặp ghép cực đại trên đồ thị hai phía. Bạn đọc nên tìm hiểu thêm về bài toán này để đưa ra những giải thuật linh hoạt hơn trong từng trường hợp cụ thể.
- Như đã nói ở trên, cách đánh giá độ phức tạp của các thuật toán trên có thể sai lệch tương đối so với thực tế. Vì vậy, khi làm những bài luồng, đôi lúc bạn có thể tính ra một độ phức tạp rất lớn, nhưng thuật toán lại chạy tốt. Ngay như bài NKFLOW ở trên, chúng ta vẫn AC được với độ phức tạp .
- Tuy chênh lệch về độ phức tạp giữa thuật Edmonds-Karp và Dinic là có thể thấy ngay, nhưng khi chạy, thuật Dinic thường cũng không cải thiện được quá nhiều. Các tác giả của Competitive Programing 3 cũng thừa nhận họ "chưa từng gặp một trường hợp đồ thị nào cho kết quả AC bằng Dinic mà chạy TLE bằng thuật Edmonds-Karp". Tuy nhiên, nếu muốn có sự tối ưu, hãy sử dụng thuật Dinic. Còn nếu bạn muốn một thuật dễ cài đặt, dễ nhớ và dễ hiểu hơn, có thể sử dụng Edmonds-Karp.
- Edmonds-Karp và Dinic là hai thuật phổ biến nhưng không phải duy nhất để tìm luồng cực đại. Bạn có thể tìm hiểu thêm về thuật push-relabel (1985) và MPM (1978) tại CP Algorithms. Gần đây, đã có những thuật tinh vi hơn tìm được luồng với độ phức tạp , như thuật của King, Rao, and Tarjan (1994), của Orlin (2012). Thậm chí, năm 2022, đã có thêm một thuật toán giải bài toán gần với bài này là min-cost flow với thời gian gần tuyến tính .
¶ Luyện tập
- BAOVE
- STNODE
- KWAY
- JOBSET
- Delivery Bears
- Soldier and Traveling
- Array and Operations
- Red-Blue Graph
- Download Speed
- Police Chase
- School Dance
Ngoài ra, bạn đọc có thể luyện tập bằng các bài tập khác có gắn tag flows trên VNOJ và các OJ khác.
¶ Tài liệu tham khảo
- Lê Minh Hoàng (2003), Giải thuật và lập trình
- Steven Halim, Felix Halim (2013), Competitive Programing 3
- CP Algorithms:
- Wikipedia (về lịch sử của các thuật toán)
- VNOI Wiki: Luồng cực đại trên mạng - Maxflow network (bài viết cũ)
- Phần chứng minh trên brilliant.org
- Reza Zadeh (2014), CME 305: Discrete Mathematics and Algorithms - Lecture 3