¶ Tham lam
Người viết:
- Nguyễn Hoàng Dương - Trường Đại học Công nghệ, ĐHQG-HN.
Reviewer:
- Đoàn Quang Huy - Trường THPT Chuyên Nguyễn Tất Thành, Quảng Ngãi.
- Nguyễn Minh Nhật - Georgia Institute of Technology.
- Nguyễn Tấn Minh - Trường Đại học Khoa học Tự nhiên, ĐHQG-HCM.
¶ Giới thiệu
Tham lam là một ý tưởng cơ bản và phổ biến trong giải thuật và lập trình, chủ yếu trong việc giải các bài toán tối ưu hoá. Ở mỗi bước chạy, thuật toán tham lam sẽ luôn chọn lựa chọn "tốt nhất" hiện tại (theo tiêu chí người thiết kế giải thuật đề ra), và không xét đến ảnh hưởng của nó đến những lựa chọn tiếp theo.
Từ những bài dễ cho đến rất khó, từ những dạng bài đơn giản cho đến đặc biệt, trong bất cứ một bước suy luận nào của bài toán, đều có thể xuất hiện tư tưởng tham lam. Điều quan trọng nhất khi áp dụng tham lam vào lời giải, là chứng minh được tính đúng đắn của quy luật tham lam -- phần tương đối khó và cũng là tinh tế, sáng tạo nhất, đòi hỏi ở người thiết kế giải thuật năng lực Toán, kinh nghiệm và ý tưởng, khả năng suy luận tốt và phán đoán nhanh nhạy.
Fun fact
Chứng minh bằng thực nghiệm (proof by AC): Trong thi đấu (đặc biệt trong ICPC), nếu ý tưởng tham lam là đủ ngắn, đủ đơn giản và ta tin rằng nó đúng (hoặc nghĩ mãi vẫn không tìm ra cách để nó sai) thì ta sẽ code luôn và chứng minh bằng việc có AC hay không.
Trong bài viết này, ở mỗi mục có các phần Ví dụ và Bài tập. Đối với các phần Bài tập, các bạn hãy cố gắng suy nghĩ thật kỹ và thử giải bài tập trước khi đọc lời giải.
¶ Những ý tưởng tham lam cơ bản
¶ Ví dụ: Movie Festival - CSES
Cho bộ phim, mỗi bộ phim kéo dài từ thời điểm đến . Bạn có thể xem được trọn vẹn nhiều nhất bao nhiêu bộ phim ?
¶ Phân tích
Đặc điểm chính của tham lam là nguyên lý cực hạn: lời giải tối ưu thường sẽ nằm ở các trường hợp biên, hoặc một nhóm nhỏ các trường hợp đặc biệt. Ta thử nghĩ một số trường hợp như vậy:
- Luôn chọn bộ phim bắt đầu sớm nhất. Ở đây ta sẽ chọn A, rồi chọn D, rồi chọn E.

- Luôn chọn bộ phim ngắn nhất, nếu có nhiều bộ phim ngắn nhất thì chọn bộ phim bắt đầu sớm hơn. Ở đây ta sẽ chọn bộ phim C, rồi đến A, rồi đến B.

- Luôn chọn bộ phim kết thúc sớm nhất. Ở đây ta sẽ chọn 3 bộ phim C, rồi đến D, rồi đến E.

Lời giải và chứng minh
Dưới đây là phản ví dụ cho 2 trường hợp 1 và 2:

Ở trường hợp 1, khi xem bộ phim bắt đầu sớm nhất, nó hoàn toàn có thể dài đến mức đè hết lên các bộ phim còn lại, còn ở trường hợp 2, nếu bộ phim ngắn nhất ấy giao nhau với quá nhiều bộ phim khác, thì cũng khiến lựa chọn không tối ưu. Việc xét trường hợp cẩn thận, tự phản biện và tìm ra phản ví dụ là một kĩ năng quan trọng khi tiếp cận bài toán bằng tham lam.
Trường hợp thứ 3 là lời giải đúng cho bài toán cổ điển này.
Thật vậy, giả sử có hai bộ phim và , và kết thúc muộn hơn . Ta xét 2 trường hợp, chọn xem hoặc .
- Nếu ta chọn xem thì sau đó ta chỉ có thể xem những bộ phim bắt đầu sau .
- Ngược lại, ta có thể xem những bộ phim bắt đầu sau . Hiển nhiên rằng số bộ phim tiếp theo ta có thể chọn xem ở trường hợp này sẽ không ít hơn trường hợp 1, nên kết quả sẽ tối ưu hơn.
Hay nói cách khác, nếu ta có thể chọn một bộ phim để xem sau , thì bộ phim đó cũng có thể xem sau , bởi vì kết thúc trước. Do đó, tập hợp các bộ phim có thể xem sau là một tập con của các bộ phim có thể xem sau , khiến cho trở thành lựa chọn tối ưu hơn.
¶ Ví dụ: Tasks and Deadlines - CSES
Bạn có công việc cần xử lý. Mỗi công việc có thời lượng và hạn chót . Bạn sẽ xử lý chúng liên tiếp và tuần tự theo thứ tự tuỳ chọn, bắt đầu từ thời điểm . Phần thưởng của một công việc là điểm (có thể âm) với là thời điểm hoàn thành công việc đó.
Nếu hành động tối ưu, phần thưởng tối đa là bao nhiêu?
Lời giải và chứng minh
Quy luật tham lam đúng là làm các công việc theo thời lượng tăng dần và không quan tâm đến hạn chót. Thật vậy, xét 2 công việc liên tiếp có thời lượng lần lượt là và :
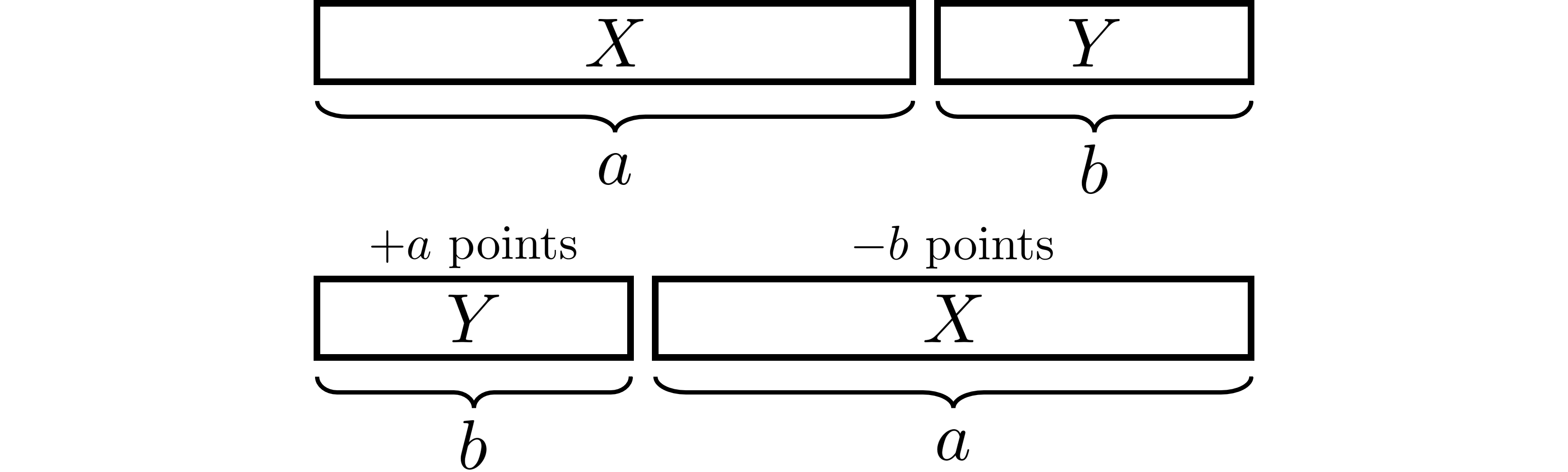
Khi này bằng việc đảo thứ tự và , ta sẽ thiệt điểm từ nhưng sẽ được thêm điểm từ nên tổng điểm sẽ tăng thêm , do đó đáp án sẽ tối ưu hơn. Ta có điều phải chứng minh.
¶ Ví dụ: Cực tiểu hoá tổng
Cho một mảng số . Tìm sao cho biểu thức sau đạt giá trị nhỏ nhất:
Ta sẽ tập trung vào hai trường hợp cơ bản và phổ biến nhất, có nhiều ứng dụng trong các bài toán: và .
¶ Trường hợp 1:
Giá trị tối ưu khi này nằm trong khoảng trung vị của mảng . Nói như vậy vì khi chẵn thì mảng sẽ có 2 trung vị, khi này tất cả nằm giữa 2 trung vị này cũng sẽ tối ưu. Nếu lẻ thì là trung vị đúng của mảng.
Chứng minh
Ta viết lại tổng bằng cách gom cặp các phần tử đầu và cuối:
Xét một cặp bất kỳ với . Theo bất đẳng thức giá trị tuyệt đối, ta luôn có:
Dấu "" xảy ra khi và chỉ khi . Do đó để nhỏ nhất toàn cục, phải thỏa mãn dấu bằng xảy ra cho tất cả các cặp
Điều này nghĩa là phải thuộc giao của tất cả các đoạn . Giao của các đoạn lồng nhau này chính là trung vị của mảng (nếu lẻ) hoặc khoảng trung vị của mảng (nếu chẵn). Tổng kết lại, ta có phải nằm trong khoảng trung vị của dãy , tức điều phải chứng minh.

Giá trị của khi thay đổi với mảng gồm số nguyên ngẫu nhiên trong khoảng , hai đường thẳng màu xanh thể hiện hai trung vị của dãy
¶ Trường hợp 2:
Giá trị tối ưu khi này sẽ là trung bình cộng của mảng .
Chứng minh
Thật vậy, ta khai triển thành
Đây là tam thức bậc hai dạng với và có dạng một parabol với bề lõm quay lên trên. Theo kiến thức toán lớp 9, đỉnh của parabol ứng với cực tiểu của đạt tại:

Giá trị của khi thay đổi với mảng gồm số nguyên ngẫu nhiên trong khoảng , đường thẳng màu xanh thể hiện trung bình cộng của dãy
¶ Ví dụ: ARC120D - Bracket Score 2
Cho dãy số nguyên có phần tử. Xét một dãy ngoặc đúng bất kì độ dài , với mỗi vị trí có ngoặc mở ta tìm vị trí ngoặc đóng tương ứng với nó và giá trị của tăng thêm một lượng . Dựng dãy ngoặc đúng ứng với dãy có giá trị lớn nhất.
Ví dụ, với dãy số và dãy ngoặc sau:

Ta có giá trị là:
Lời giải và chứng minh
Một cách khác để áp dụng nguyên lý cực hạn, là thử tìm cận trên/cận dưới của đáp án theo yêu cầu đề bài, và chứng minh/chỉ ra cách dựng ra trường hợp thoả mãn cận đó.
Phần 1: Cận trên
Tổng giá trị của dãy ngoặc là . Ta biết rằng . Do đó, giá trị của dãy ngoặc có thể viết lại thành:
Theo đó, giá trị tối đa không thể vượt quá: (Tổng số lớn nhất) - (Tổng số nhỏ nhất). Ta chứng minh luôn tồn tại dãy ngoặc đạt được giá trị này.
Phần 2: Dựng dãy
Ta cần chỉ ra một cách phân chia dãy phần tử thành tập ( phần tử nhỏ nhất) và tập ( phần tử lớn nhất) và một dãy ngoặc đúng sao cho mỗi cặp ngoặc đều gồm một phần tử thuộc và một phần tử thuộc .
Ta sử dụng cấu trúc dữ liệu stack. Xét phần tử thứ trong mảng:
- Nếu stack rỗng, hoặc phần tử hiện tại cùng tập với đỉnh stack, ta thêm chỉ số vào đỉnh stack, khi này vị trí thứ sẽ là ngoặc mở.
- Nếu stack không rỗng và phần tử thứ khác tập với phần tử ở đỉnh stack có chỉ số , ta ghép được với là cặp ngoặc tương ứng, với là ngoặc mở và là ngoặc đóng.
Phần 3: Chứng minh
Ta chứng minh cách dựng trên thoả mãn tính chất của dãy ngoặc đúng và cận trên của bài toán:
- Ở mọi thời điểm, stack chỉ chứa các phần tử của cùng 1 tập, hoặc cùng thuộc hoặc cùng thuộc . Ta chỉ ghép 2 phần tử lại nếu chúng khác tập, do đó khi kết thúc việc dựng dãy, stack sẽ rỗng. Thật vậy... Ta đã ghép hết được cặp phần tử, mỗi cặp gồm 2 phần tử thuộc 2 tập khác nhau nên giá trị thu được chính là cận trên của bài toán.
- Thuật toán dựng dãy ngoặc ở phần 2 có các tính chất sau:
- Số phần tử của stack ở mỗi thời điểm đại diện cho độ sâu hiện tại đang duyệt đến của dãy ngoặc.
- Mỗi thao tác duyệt phần tử đều làm thay đổi độ sâu của stack, hoặc nếu ghép được, hoặc nếu đẩy thêm vào stack. Stack không bao giờ
pop(xóa) phần tử khi đang ở trạng thái rỗng. - Stack bắt đầu và kết thúc ở trạng thái rỗng (đã chứng minh ở 1).
- Từ nhận xét 2, ta thấy rằng số phần tử trong stack ở mỗi thời điểm đại diện cho độ sâu của dãy ngoặc ở thời điểm đó và luôn không âm, stack luôn bắt đầu và kết thúc ở trạng thái rỗng, do đó dãy ngoặc tương ứng dựng được thoả mãn tính chất của dãy ngoặc đúng. Ta có điều phải chứng minh.
3 tính chất trên thoả mãn các tính chất của dãy ngoặc đúng, nên dãy ngoặc mà thuật toán dựng ra là dãy ngoặc đúng.
Ta có điều phải chứng minh.
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n;
cin >> n;
// Lưu giá trị và chỉ số ban đầu để sort
vector<pair<int, int>> a(2 * n);
for (int i = 0; i < 2 * n; ++i) {
cin >> a[i].first;
a[i].second = i;
}
// Sắp xếp để phân loại N số nhỏ và N số lớn
sort(a.begin(), a.end());
// type[i] = 0 nếu a[i] thuộc nhóm nhỏ, 1 nếu thuộc nhóm lớn
vector<int> type(2 * n);
for (int i = 0; i < n; ++i) type[a[i].second] = 0; // N số nhỏ nhất
for (int i = n; i < 2 * n; ++i) type[a[i].second] = 1; // N số lớn nhất
stack<int> st; // Lưu loại (0 hoặc 1) của ngoặc mở chưa được ghép
string ans = "";
for (int i = 0; i < 2 * n; ++i) {
// Nếu stack không rỗng và phần tử hiện tại khác loại với đỉnh stack
// => Ghép được cặp |nhỏ - lớn| => Đóng ngoặc
if (!st.empty() && st.top() != type[i]) {
ans += ')';
st.pop();
}
// Ngược lại: Cùng loại hoặc stack rỗng => Phải mở ngoặc mới
else {
ans += '(';
st.push(type[i]);
}
}
cout << ans << endl;
return 0;
}
¶ Cấu trúc con tối ưu
Một bài toán có cấu trúc con tối ưu nếu như nghiệm tối ưu của nó có thể thu được từ nghiệm tối ưu của các bài toán con.
Cấu trúc con tối ưu gọi là có tính chất tham lam nếu như ở mỗi bài toán con ta đều có thể chọn đi theo hướng tối ưu cục bộ mà dẫn đến tối ưu toàn cục ở bài toán ban đầu. Tính chất trên gợi mở rằng ta có thể dùng tư tưởng quy nạp để tìm ra bản chất tham lam của bài toán, cũng như chứng minh tính đúng đắn của thuật toán tham lam.
¶ Ví dụ: Chia tiền xu
Tìm số đồng xu ít nhất cần để trả được đồng bằng các đồng tiền có mệnh giá .
Lời giải
Với tập như trên, việc tham lam luôn chọn mệnh giá lớn nhất để trả sẽ cho kết quả tối ưu. Chẳng hạn với mệnh giá , chừng nào thì ta sẽ luôn trả bằng 5 đồng, đưa về bài toán con với mệnh giá . Rồi ta làm tương tự với các mệnh giá nhỏ hơn cho đến hết.
Tập các mệnh giá mà ta có thể tham lam để trả được ít đồng xu nhất gọi là hệ chuẩn tắc (canonical system), các bạn có thể dễ thấy sự hữu ích và tiện lợi của nó trong hệ thống tiền tệ của các quốc gia hiện tại. Còn với các tập mệnh giá khác (không phải chuẩn tắc), việc tham lam như trên sẽ không cho kết quả tối ưu, mà ta phải sử dụng Quy hoạch động.
¶ Bài tập: Missing Coin Sum - CSES
Cho 1 tập các đồng xu có mệnh giá . Tìm mệnh giá nhỏ nhất không trả được bằng một tập con phân biệt của các đồng xu trên. Ví dụ với tập các đồng xu thì ta có thể trả được nhưng không có tập con nào trả được , nên đáp án là .
Lời giải
Giả sử . Ta coi và . Đặt . Khi đó ta tìm giá trị đầu tiên sao cho . Khi đó chính là đáp án.
Chứng minh:
Bước cơ sở:
Xét đồng xu đầu tiên . Ta có .
- Nếu : Theo công thức, . Đáp án là 1. Điều này đúng vì nếu đồng xu nhỏ nhất lớn hơn 1, ta không thể tạo ra 1.
- Nếu : Ta tạo được đoạn . Ta tiếp tục xét các đồng xu sau.
Bước quy nạp:
Giả sử với đồng xu đầu tiên, ta đã tạo được mọi giá trị nguyên liên tiếp trong đoạn (bao gồm 0 là tập rỗng). Xét đồng xu tiếp theo là . Khi thêm vào, các giá trị mới ta có thể tạo ra là:
Trong đó ta tạo thêm được đoạn giá trị: . Lúc này, tập hợp tất cả các giá trị có thể tạo được là hợp của hai đoạn:
Ta xét hai trường hợp của :
- . Khi đó, đoạn thứ hai bắt đầu tại , mà . Điều này có nghĩa là đoạn thứ hai sẽ nối tiếp hoặc giao với đoạn thứ nhất. Hợp của chúng sẽ là một đoạn liên tục:
Ta vẫn tạo được mọi giá trị từ đến và quy nạp tiếp tục.
- . Ta có không nằm trong đoạn và nhỏ hơn (theo giả thiết trường hợp này), nên nó cũng không nằm trong đoạn . Suy ra không có cách nào tạo ra được . Theo giả thiết quy nạp, ta đã có cách tạo được hết các giá trị , nên chính là giá trị nhỏ nhất không thể tạo được. Ta có điều phải chứng minh.
Trong thực tế, có nhiều bài toán phổ biến tồn tại cấu trúc con tham lam, và lời giải cho các bài toán đó là những thuật toán đẹp mà chúng ta đang sử dụng hằng ngày. Chẳng hạn như thuật toán Kruskal tìm cây khung nhỏ nhất, thuật toán Dijkstra tìm đường đi đơn tối ưu trên đồ thị không có cạnh âm, cho đến các thuật toán luồng như Ford-Fulkerson, Dinic. Cũng có những bài toán mà chúng ta có thể giải dưới cả góc nhìn của Tham lam và Quy hoạch động, điển hình là thuật toán tìm đoạn con có tổng lớn nhất Kadane. Khi này, cài đặt tham lam thường rất gọn và đẹp, còn cài đặt Quy hoạch động lại có thể linh hoạt với nhiều biến thể khác nhau của cùng một bài toán.
¶ Exchange Argument - Lập luận hoán đổi
Ở các bài toán cơ bản chúng ta đã biết về thứ tự tham lam đơn giản. Tuy nhiên có những bài toán mà cấu trúc thứ tự của đáp án tối ưu không dễ để nhìn ra ngay. Khi này, ta sẽ đi từ trường hợp đơn giản khi chỉ có phần tử. Bằng việc hoán đổi 2 phần tử và biến đổi tương đương các đại lượng, ta có thể biện luận được thứ tự phức tạp và tối ưu để xử lý các phần tử. Đây cũng là phương pháp phổ biến để chứng minh tính đúng đắn của thuật toán tham lam.
¶ Ví dụ: Chia vàng
Có một ông vua và ông quan. Ông vua muốn chia thưởng cho các ông quan theo quy tắc sau:
- Ông vua viết lên tay trái số nguyên và tay phải mình số nguyên . Với mỗi ông quan, ông quan thứ viết lên tay trái số và tay phải số .
- Sau khi viết xong, ông vua và ông quan xếp thành 1 hàng dọc, ông vua luôn đứng đầu hàng.
- Sau khi xếp hàng, ông quan thứ sẽ được nhận số vàng bằng tích tất cả số bên tay trái của những người đứng trước ông ta (cả ông vua và ông quan) chia cho số ở tay phải ông ta (làm tròn xuống).
Tìm cách để ông vua xếp thứ tự ông quan đứng sau mình sao cho số vàng của ông quan được thưởng nhiều nhất là ít nhất.
Ý tưởng và lời giải
Gọi đứng trước , khi này ông quan thứ nhận được vàng còn ông quan thứ nhận được vàng.
Nếu ta đảo chỗ hai ông quan và thì khi này ông nhận vàng còn ông nhận được vàng.
Việc đảo vị trí sẽ khiến đáp án tối ưu hơn nếu và chỉ nếu:
tương đương với:
Trong thực tế, khi cài đặt, ta sẽ viết lại để biểu thức không có phép chia, qua đó loại bỏ được vấn đề so sánh số thực hoặc chia cho 0:
Trong thực tế, Exchange Argument còn được sử dụng phổ biến trong các bài toán Quy hoạch động, chủ yếu là để tìm thứ tự trong các bài toán về việc chọn một tập con tối ưu mà thứ tự thêm các phần tử sẽ ảnh hưởng đến đáp án. Ta cùng đến với một bài toán như vậy:
¶ Bài tập: ABC366F - Maximum Composition
Cho hàm tuyến tính . Tính giá trị lớn nhất của hàm hợp với là các bộ số khác nhau.
Giới hạn: .
Lời giải và chứng minh
Phần 1: Exchange Argument
Giả sử ta đã chọn được hàm hợp có hàm số tối ưu. Ta cần xác định thứ tự áp dụng để đạt giá trị lớn nhất. Xét 2 hàm số và được chọn. Giả sử ta áp dụng chúng liền kề nhau lên giá trị hiện tại :
- Áp dụng trước, sau .
- Áp dụng trước, sau .
Để thứ tự trước, sau tốt hơn, ta cần có:
Hàm nào có giá trị lớn hơn sẽ được ưu tiên áp dụng trước. Ta sẽ sắp xếp các hàm số theo biểu thức trên, qua đó tạo thêm được giả thiết cho bài toán (từ các bộ bất kì thành các bộ có chỉ số tăng dần). Khi này ta có thể giải bằng motif Quy hoạch động quen thuộc.
Phần 2: Quy hoạch động
Gọi là giá trị lớn nhất tạo được với hàm hợp của hàm số. Duyệt qua danh sách hàm số đã sắp xếp: Với mỗi hàm , ta xem xét việc áp dụng hàm này sau khi đã áp dụng hàm trước đó. Công thức chuyển trạng thái như sau:
Khởi tạo: (đề bài cho ), các vị trí khác .
Cài đặt
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const long long INF = 2e18;
struct Func {
int a, b;
};
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n, k;
cin >> n >> k;
vector<Func> funcs(n);
for (int i = 0; i < n; ++i) {
cin >> funcs[i].a >> funcs[i].b;
}
// Sắp xếp theo Exchange Argument
// Hàm nào có độ ưu tiên cao hơn (B/(A-1) lớn hơn) sẽ được xét trước
sort(funcs.begin(), funcs.end(), [](const Func& x, const Func& y) {
// So sánh: x.b / (x.a - 1) > y.b / (y.a - 1)
// Chuyển vế nhân để tránh chia cho 0 và sai số số thực
return (long long)x.b * (y.a - 1) > (long long)y.b * (x.a - 1);
});
// DP: dp[j] = Giá trị lớn nhất của hàm hợp đã có j hàm số
vector<long long> dp(k + 1, -INF);
dp[0] = 1; // Giá trị khởi đầu đề bài cho là 1
// Với mỗi hàm, ta xem xét thêm nó vào hợp của j - 1 hàm đã áp dụng trước đó
for (const auto& f : funcs) {
// Duyệt ngược để đảm bảo mỗi hàm chỉ dùng 1 lần cho mỗi trạng thái
for (int j = k; j >= 1; --j) {
if (dp[j - 1] > -INF) {
// Thử áp dụng hàm f vào kết quả của chuỗi j-1 hàm trước đó
long long next_val = f.a * dp[j - 1] + f.b;
if (next_val > dp[j]) {
dp[j] = next_val;
}
}
}
}
cout << dp[k] << "\n";
return 0;
}
¶ Regrettable Greedy - Sửa lại lựa chọn
Có một số lúc mà việc ta liên tục tham lam tối ưu hoá lựa chọn ở hiện tại có thể vi phạm ràng buộc của bài toán hoặc bị chệch ra khỏi nghiệm tối ưu. Nhưng bằng việc tạo ra cơ chế để sửa lại lựa chọn thì lại có thể đạt được lời giải không chỉ hợp lệ và tối ưu, mà còn đẹp và tinh tuý.
¶ Ví dụ: Time Travel
Cho một mảng các số nguyên dương. Tìm cách gán dấu âm cho nhiều phần tử nhất có thể sao cho vẫn đảm bảo mọi tổng tiền tố của mảng đều dương.
Ý tưởng và lời giải
Khi duyệt qua từng phần tử của mảng, ta ban đầu luôn ưu tiên gán dấu âm cho nó để tăng số lượng phần tử âm, đồng thời đẩy giá trị âm này vào một Priority Queue và cập nhật tổng tiền tố hiện tại.
Nếu tại bất kỳ bước nào việc đổi dấu vi phạm điều kiện tổng tiền tố dương, ta có thể quay lại, đưa những phần tử ta vừa gán dấu âm trước đó về như cũ. Để tối ưu thì ta sẽ chọn số âm trong Priority Queue đang có giá trị tuyệt đối lớn nhất và đổi lại nó về dương, khi này ta sẽ có nhiều khả năng hơn để gán dấu âm cho các phần tử tiếp theo.
Sau khi duyệt hết mảng, số lượng phần tử còn lại trong Priority Queue chính là số lượng số âm tối đa thỏa mãn đề bài. Độ phức tạp là .
¶ Bài tập: CF865D - Buy Low Sell High
Đây cũng là bài ABC250G - Stonks.
Bạn có thông tin giá cổ phiếu của ngày tiếp theo. Mỗi ngày bạn có thể chọn bán 1 đơn vị cổ phiếu với giá của ngày hôm đó, hoặc mua tích trữ 1 đơn vị cổ phiếu với giá của ngày hôm đó để bán sau, hoặc không làm gì. Lúc bắt đầu bạn không có cổ phiếu và sau ngày phải giao dịch được hết cổ phiếu đang có. Hỏi lợi nhuận tối đa thu được là bao nhiêu?
Ý tưởng và lời giải
Đây là bài toán kinh điển của kĩ thuật Quản lý đồ thị hàm Quy hoạch động (hay còn gọi là Slope Trick). Tuy nhiên bài toán này lại có 1 góc nhìn khác, một hướng giải rất đẹp bằng kĩ thuật sửa lại lựa chọn (và cách cài đặt trùng hợp thay lại rất giống Slope Trick).
Trong bài toán này, chúng ta sẽ "thử" giao dịch nếu thấy có lãi, nhưng sẽ lưu lại thông tin để hoàn tác giao dịch này và sửa sai trong tương lai. Ta dựng một Priority Queue thể hiện danh sách quyền mua. Tại ngày với giá , ta làm như sau:
- Ta luôn coi là một cơ hội mua tiềm năng và thêm vào PQ. Nếu lớn hơn quyền mua thấp nhất hiện có trong quá khứ (), ta thực hiện khớp lệnh mua tại và bán tại để kiếm lời ngay lập tức: . Việc ưu tiên chọn để khớp lệnh là chiến lược tốt nhất vì nó không chỉ tối đa hóa lợi nhuận tức thời mà còn an toàn hơn về điều kiện giao dịch (vì dễ khớp lệnh hơn). Quan trọng nhất, việc "chốt lãi" sớm này không làm mất nghiệm tối ưu toàn cục, bởi bất kỳ lợi ích tiềm năng nào của việc để dành cho tương lai đều có thể được bù đắp bởi cơ chế sửa sai ở bước sau.
- Đây là điểm mấu chốt. Khi ta quyết định khớp lệnh mua ở với lệnh bán ở , ta vẫn đẩy lại vào PQ. Thao tác này đóng vai trò như một công cụ toán học biến đổi trạng thái từ "vừa bán tại " thành một "quyền mua ảo tại ". Nếu trong tương lai xuất hiện giá bán lời hơn , ta sẽ dùng chính quyền mua ảo này để khớp lệnh (sửa lại lựa chọn). Khi đó, tổng lợi nhuận của chuỗi giao dịch sẽ là tổng đại số: . Điều này chứng tỏ việc sửa lại lựa chọn tương đương với việc ta đã đưa ra quyết định đúng đắn (bán ở ) ngay từ đầu mà không vi phạm ràng buộc nào của bài toán.
Cài đặt
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n;
cin >> n;
// Min-Priority Queue để lưu giá các quyền mua (cũng như để sửa lại lựa chọn)
priority_queue<long long, vector<long long>, greater<long long>> pq;
long long total_profit = 0;
for (int i = 0; i < n; ++i) {
long long current_price;
cin >> current_price;
// Luôn luôn push giá hiện tại vào PQ.
// Ý nghĩa: Ta luôn có quyền mua cổ phiếu này tại ngày hôm nay.
pq.push(current_price);
// Kiểm tra xem có thể bán (hoặc sửa lại lựa chọn) để có lời không
if (pq.top() < current_price) {
// Giá thấp nhất trong quá khứ
long long buy_price = pq.top();
// Cộng lợi nhuận giả định vào tổng
total_profit += current_price - buy_price;
// Xóa giá mua đó đi (vì đã được dùng để khớp với lệnh bán này)
pq.pop();
// Cơ chế sửa lại lựa chọn: Push giá cổ phiếu hiện tại vào lại PQ
// Ý nghĩa: Ta vừa bán ở 'current_price', nhưng ta trao cho tương lai quyền
// "mua lại" chính cổ phiếu này với giá 'current_price' để bán ở mức cao hơn.
// Về toán học: (p_new - p_old) + (p_future - p_new) = p_future - p_old.
pq.push(current_price);
}
}
cout << total_profit << endl;
return 0;
}
Bonus
Vì có cùng bản chất, kĩ thuật sửa lại lựa chọn có thể được chứng minh và tổng quát hoá bằng việc mô hình hoá bài toán thành dạng luồng cực đại chi phí cực tiểu. Ngược lại, trong bài toán mà đồ thị luồng min-cost dựng ra có dạng đặc biệt, ta có thể giải nó một cách hiệu quả bằng kĩ thuật sửa lại lựa chọn với độ phức tạp thấp hơn hẳn. Các bạn có thể đọc thêm về chuyên đề này trong tài liệu phụ lục.
¶ Kĩ thuật cài đặt
Việc tạo ra cấu trúc thứ tự cho dữ liệu trong thuật toán tham lam có 2 cách phổ biến sau:
- Sắp xếp (bằng một hàm so sánh nào đó)
- Sử dụng các cấu trúc dữ liệu duy trì thứ tự sẵn có của C++ STL:
set,multiset,map,priority_queue,...
¶ Sắp xếp
Hàm std::sort trong C++ có cú pháp như sau:
// ví dụ, với vector s
sort(s.begin(), s.end(), func) // sort không giảm
sort(s.rbegin(), s.rend(), func) // sort không tăng
với func là hàm so sánh (comparator) tuỳ chọn giữa 2 phần tử bất kì trong mảng. Nếu ta không thiết lập hàm func này, thì kiểu dữ liệu mà ta sử dụng phải có định nghĩa phép toán < của nó. Chẳng hạn, trong bài toán Chia vàng ở phần Exchange Argument, ta có thể cài đặt như sau:
struct Info {
int a, b;
bool operator<(const Info &x) const {
return max(x.b, a * b) < max(b, x.a * x.b);
} // so sánh phần tử này với một phần tử khác (gọi là x)
};
Lưu ý
Nếu hai phần tử được so sánh bằng nhau, thì cài đặt hàm so sánh phải trả vềfalse, nếu không thứ tự các phần tử có thể không khớp với thứ tự so sánh.
¶ Sử dụng STL
Đối với ngôn ngữ C++, ta có thể thiết lập hàm so sánh cho các cấu trúc dữ liệu STL: set, priority_queue, map,... bằng functor-comparator (đối tượng hàm so sánh). Có hai loại chính:
less<T>: ứng vớioperator <, mặc định các cấu trúc dữ liệu STL sẽ dùng functor này.greater<T>: ứng vớioperator >
Chẳng hạn, priority_queue bình thường sẽ luôn trả về phần tử lớn nhất, bạn có thể khai báo priority_queue<int, vector<int>, greater<int>> để lấy phần tử nhỏ nhất.
Khi khai báo 1 struct, việc định nghĩa phép toán thứ tự < hoặc > trong struct sẽ giúp ta có thể sử dụng chúng ngay lập tức trong các cấu trúc dữ liệu STL.
Đối với C++11 trở đi, ngoài cách khai báo functor như ở trên, ta có thể khai báo dưới dạng lambda rất gọn và nhúng vào bằng từ khoá decltype (declared type):
auto cmp = [](int a, int b) { return ... };
std::set<int, decltype(cmp)> s;
std::priority_queue<int, vector<int>, decltype(cmp)> pq;
¶ Tham lam trong thực chiến
Trong phần này, chúng ta sẽ cùng đào sâu vào 2 bài toán tham lam hay đã xuất hiện trong kì thi ICPC Regional 2024 tại Hà Nội.
¶ Bài tập: ICPC 2024 Regional Hanoi bài L: Locomotive Lane Logistics
Cho một đường ray có độ dài và truy vấn. Mỗi truy vấn có 1 trong 2 dạng:
+ l v: thêm 1 tàu có độ dài và vận tốc vào lịch trình.- l v: xoá 1 tàu có độ dài và vận tốc khỏi lịch trình, đảm bảo trong lịch trình hiện tại có ít nhất 1 tàu như vậy.
Mỗi con tàu có phần mui và phần đuôi, khoảng cách giữa mui và đuôi của tàu chính là độ dài của nó. Con tàu sẽ xuất phát với mui chạm vạch xuất phát, đi đều liên tục với vận tốc về phía vạch kết thúc và chỉ ra khỏi đường ray khi đuôi rời khỏi vạch kết thúc. Mỗi con tàu ta có thể chọn cho nó thời điểm xuất phát là số thực bất kì.
Sau mỗi truy vấn, tính tổng thời gian ít nhất để đưa toàn bộ tàu trong danh sách ra khỏi đường ray mà không xảy ra tai nạn. Tai nạn có thể xảy ra giữa 2 tàu ở thời điểm mui của tàu đi sau đâm vào đuôi của tàu đi trước, vận tốc của tàu đi sau lớn hơn tàu đi trước và tàu đi trước chưa ra khỏi đường ray. In ra đáp án tối ưu (luôn có dạng là số hữu tỉ) theo modulo .
Giới hạn: .
Lời giải
Qua cảm nhận, ta có thể rút ra 2 nhận xét tham lam đầu tiên về đáp án tối ưu:
- Nếu 2 tàu có cùng vận tốc, thì chúng có thể đi nối đuôi nhau như là 1 tàu (vẫn thoả mãn điều kiện không xảy ra tai nạn), nên ta có thể giả sử vận tốc của tất cả các tàu đều khác nhau.
- Để tối thiểu hoá tổng thời gian, các tàu cần di chuyển nối tiếp nhau khít nhất có thể, tàu chậm sẽ đi trước, rồi sau một khoảng thời gian tối ưu ta sẽ cho tàu nhanh hơn xuất phát và đuổi theo sau. Một cách để chứng minh nhận xét này, là tàu đi sau đã tận dụng triệt để khoảng thời gian tàu đi trước chiếm dụng đường ray để tranh thủ di chuyển được một khoảng cách nhất định.
Tiếp theo đó, bằng việc ngồi nháp toán và chứng minh công thức ta rút ra nhận xét quan trọng nhất của bài toán:
- Giả sử có 2 tàu và với . Ta cho đi trước, đi sau và sẽ có xu hướng đuổi kịp. Để tối ưu thời gian, ta căn chỉnh sao cho ngay thời điểm đuôi rời khỏi đường ray thì mui của cũng vừa chạm vạch kết thúc. Theo đó ta có giãn cách thời gian tối ưu giữa 2 tàu:
- Áp dụng nhận xét trên cho tàu, thì tổng thời gian tối ưu là:
Do đó ta chỉ cần duy trì 2 giá trị sau qua các thao tác thêm và xoá tàu khỏi danh sách:
- Vận tốc của tàu chậm nhất trong danh sách hiện tại, có thể dùng
multisethoặcpriority queue. - Tổng của các tàu đang có trong danh sách hiện tại.
Độ phức tạp cho mỗi truy vấn là .
¶ Bài tập: ICPC 2024 Regional Hanoi bài K: Kangokutou Exodus
Cho một mê cung gồm hành lang vuông góc liên tiếp nhau, mỗi hành lang có độ dài . Bạn đứng ở điểm bắt đầu của hành lang .
Trước khi vượt mê cung. bạn có thể chọn trước độ dài tốc biến nguyên để di chuyển từ điểm bắt đầu của hành lang đến điểm kết thúc của hành lang .
Ở mỗi thời điểm nguyên bạn sẽ tốc biến đúng đơn vị độ dài về phía trước trong giây, nếu cú tốc biến này không chuẩn (khoảng cách từ điểm bạn tốc biến đến điểm cuối của hành lang hiện tại nhỏ hơn đơn vị) thì bạn sẽ tốc biến đến điểm cuối của hành lang và bị choáng giây, điều này áp dụng cả với hành lang cuối. Ngược lại, bạn có thể tốc biến tiếp ngay lập tức mà không bị choáng.
Tính thời gian ngắn nhất có thể để ra khỏi mê cung khi chọn tối ưu.
Giới hạn: .
Lời giải
Vì quá trình di chuyển qua các hành lang là độc lập với nhau, ta có thể sắp xếp lại các hành lang theo thứ tự: .
Chúng ta bắt đầu với một số nhận xét tham lam như sau về đáp án tối ưu:
- Với cho trước thì ta có công thức tổng thời gian hoàn thành:
là kí hiệu Iverson của biểu thức boolean , với nếu đúng và nếu sai.
- Ta nhận thấy rằng đáp án tối ưu có cận dưới và cận trên hiển nhiên là và . Cận dưới xảy ra khi toàn bộ bằng nhau, khi đó ta chọn , còn cận trên xảy ra khi ta cho .
- tối ưu khi và chỉ khi là một trong các . Thật vậy, giả sử giá trị tối ưu là không trùng với bất cứ nào. Khi này với các thì ta sẽ mất đúng giây để đi qua, còn với thì ta sẽ mất ít nhất giây để đi qua. Do đó . do đó không tối ưu. Ta có điều phải chứng minh.
Nhận xét thứ 3 gợi ý rằng chúng ta cần duyệt qua tất cả các khác nhau và tính nhanh được . Chúng ta chia mảng thành 3 phần:
- Phần mà , mỗi mất giây.
- Phần , mỗi mất giây.
- Phần còn lại với mỗi mất giây.
Mấu chốt của bài toán là tính phần 3 đủ nhanh khi 2 phần trước ta có thể tính trong . Và thật ra, cách đủ nhanh lại là một ý tưởng tham lam và đặt cận đơn giản:
#include <bits/stdc++.h>
using namespace std;
// Hàm tính thời gian đi qua hành lang độ dài len với bước nhảy m
// Công thức: ceil(len/m) + (1 nếu len không chia hết cho m)
int calculate_cost(int len, int m) {
if (len % m == 0) {
return len / m;
} else {
return (len / m) + 2; // 1 bước cuối + 1 giây choáng
}
}
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
// Sắp xếp để gom nhóm các hành lang có cùng độ dài
// và dễ dàng xử lý các phần tử nhỏ hơn/lớn hơn.
sort(a.begin(), a.end());
// Khởi tạo kết quả ban đầu: trường hợp tệ nhất mỗi hành lang tốn 2s
// (ví dụ chọn m > max(a_i), tất cả đều nhảy quá đà và bị choáng)
long long min_total_time = 2LL * n;
for (int i = 0; i < n;) {
int m = a[i]; // Chọn độ dài bước nhảy m bằng độ dài hành lang hiện tại
// Tìm vị trí cuối cùng có giá trị bằng a[i]
// Đoạn [i, j] là các hành lang có độ dài bằng m (tốn 1s)
int j = i;
while (j < n && a[j] == m) {
j++;
}
// j lúc này là chỉ số của phần tử đầu tiên > m (hoặc n)
// Tính chi phí cơ sở cho lần chọn m này:
// 1. Các hành lang < m: tốn 2s (nhảy quá đà ngay bước 1)
// 2. Các hành lang = m (từ i đến j-1): tốn 1s
// 3. Các hành lang > m (từ j đến n-1): giả sử tạm tính tối thiểu là 2s
// (Thực tế sẽ >= 2s. Ta sẽ cộng phần chênh lệch sau)
long long current_time = i * 2 + (j - i) * 1 + (n - j) * 2;
// Tối ưu: Duyệt các phần tử lớn hơn m từ lớn về bé.
// Cộng thêm chi phí thực tế chênh lệch so với giả định (2s).
// Nếu tổng vượt quá kết quả tốt nhất hiện có thì dừng ngay.
for (int k = n - 1; k >= j; --k) {
int actual_cost = calculate_cost(a[k], m);
current_time += (actual_cost - 2);
if (current_time >= min_total_time) {
break;
}
}
min_total_time = min(min_total_time, current_time);
// Chuyển sang nhóm độ dài tiếp theo
i = j;
}
cout << min_total_time << "\n";
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int tc;
cin >> tc;
while (tc--) solve();
return 0;
}
Ý tưởng tóm gọn như sau: Ở một thời điểm bất kì, giá trị của min_total_time là ngưỡng quyết định xem l[i] hiện tại có tối ưu hơn không. Để có thể quyết định nhanh, ta duyệt qua các giá trị từ lớn đến nhỏ, nếu đến một lúc nào đó current_time lớn hơn ngưỡng tối ưu hiện tại thì ta có thể loại luôn l[i].
Độ phức tạp của 2 vòng lặp khi này không phải mà là . Để chứng minh nhận định này, ta sẽ đánh giá về tổng số lần duyệt trung bình cần để kết thúc thuật toán:
- Với mỗi độ dài phân biệt , tất cả các hành lang có độ dài thuộc 2 khoảng và sẽ tốn giây để di chuyển.
- Số hành lang có thể di chuyển trong giây là , còn lại với độ dài ta sẽ tốn đúng giây để di chuyển.
- Từ 2 điều trên, kết hợp với nhận xét 3 đã chứng minh, ta thấy rằng với mỗi phân biệt, ta sẽ chỉ duyệt qua nhiều nhất là giá trị để biết được là đang xét có tối ưu hơn không.
Do đó độ phức tạp của bước tính này là với mọi phân biệt của mảng và là . Độ phức tạp cuối cùng của bài là do sắp xếp.
¶ Lời kết
Tham lam không chỉ là một dạng bài. Nó là một hệ tư tưởng luôn len lỏi trong giải thuật, và có thể xuất hiện bất cứ đâu trong các bài toán, trong một bước, nhiều bước giải hoặc toàn bộ bài toán. Đây thường là phần hay, độc đáo trong các kì thi, thử thách sự nhanh nhạy, kinh nghiệm và sáng tạo của thí sinh, cũng như trí tuệ của người ra đề. Hi vọng bài viết này đã phần nào đó truyền tải được nét đẹp của tư tưởng tham lam, để các bạn hào hứng chinh phục những bài toán hay hơn và khó hơn trong tương lai.
¶ Bài tập vận dụng
¶ Tham lam cơ bản
- ICPC SEERC 2023 bài J - Jackpot
- CF1896C - Matching Arrays
- CF1779C - Least Prefix Sum
- ICPC 2025 vòng Quốc gia bài F - Feast of Delicacy
¶ Exchange Argument
- CF632C - The Smallest String Concatenation
- ICPC 2025 vòng Quốc gia bài B - Blowing Balloons
- CF1043E - Train Hard, Win Easy
- AtCoder - Manga Market
- AtCoder - Zabuton
- Singapore NOI 2022 - Gym Badges
¶ Regrettable Greedy
- CF1526C2 - Potion
- CF1974G - Money Buys Less Happiness Now
- CF730I - Olympiad in Programming and Sports
- CF3D - Least Cost Bracket Sequence
¶ Bài khó
- CF436E - Cardboard Boxes
- AGC072A - Rhythm Game
- IOI 2020 ngày 1 bài 3 - Carnival Tickets
- CF1793E - Velepin and Marketing
- NOI 2019 - Sequence
- ICPC World Finals 2018 bài C - Conquer the World