¶ Phân tích thừa số nguyên tố
Người viết:
- Nguyễn Minh Hiển - Trường Đại học Công nghệ, ĐHQGHN
Reviewer:
- Lê Minh Hoàng - Trường Đại học Khoa học Tự nhiên - ĐHQG TP.HCM
- Nguyễn Minh Nhật - THPT chuyên Khoa học Tự nhiên, ĐHQGHN
- Võ Đức Đoàn - THPT Chuyên Nguyễn Tất Thành - Kon Tum
¶ Bài toán
Phân tích thừa số nguyên tố là một bài toán cơ bản với mục tiêu là phân tích một số nguyên dương thành tích của các thừa số nguyên tố.
Cụ thể, cho một số nguyên dương (với ), ta cần tìm một dãy các số nguyên tố sao cho , trong đó:
- là các số nguyên tố và đôi một phân biệt.
- Mỗi là số mũ nguyên dương của trong phân tích thừa số của ,
- Các số nguyên tố nên được sắp xếp theo thứ tự tăng dần.
Ví dụ: với , ta cần phân tích
¶ Thuật toán ngây thơ
Nhận xét: Một số nguyên dương chỉ có tối đa một ước nguyên tố lớn hơn .
Chứng minh
Giả sử có hai ước nguyên tố lớn hơn , gọi là và .
- Vì và đều là ước nguyên tố của , nên phải chia hết cho và . Điều này có nghĩa là:
- Theo giả thiết, và . Tích của hai số này là:
- Như vậy sẽ dẫn đến mâu thuẫn
Do đó, ta chỉ cần duyệt tìm các ước nguyên tố của trong và chia dần dần cho các ước số này (Nếu thì ta chỉ cần phân tích ). Sau khi duyệt xong, số còn lại sẽ là hoặc một số nguyên tố.
Trên thực tế, để đơn giản hóa mã nguồn khi triển khai thuật toán, ta sẽ duyệt qua tất cả các số nguyên từ 2 đến phần nguyên của căn bậc hai của , bao gồm cả các số hợp.
Tại sao lại như vậy?
Giả sử tại một thời điểm, ta duyệt đến một số hợp có dạng , trong đó là các thừa số nguyên tố. Khi chia hết cho , điều này có nghĩa là cũng đã chia hết cho một trong các thừa số nguyên tố . Các thừa số này sẽ được xử lý bằng phép chian /= dtrong quá trình duyệt các số nhỏ hơn .
Thuật toán này cho ta phân tích thừa số nguyên tố trong .
vector<long long> trial_division1(long long n) {
vector<long long> factorization;
for (long long d = 2; d * d <= n; d++) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
¶ Bánh xe phân tích - Wheel Factorization
Bánh xe phân tích là một cải tiến cho thuật toán cơ bản ở trên.
Xem xét tối ưu sau:
Nếu lẻ thì chúng ta không cần duyệt các số chẵn trong .
Điều này sẽ giảm được số lượng số cần kiểm tra.
Về cài đặt, sau khi kiểm tra , chúng ta duyệt từ và bỏ qua các số chẵn.
vector<long long> trial_division2(long long n) {
vector<long long> factorization;
while (n % 2 == 0) {
factorization.push_back(2);
n /= 2;
}
for (long long d = 3; d * d <= n; d += 2) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
Tương tự, nếu không phải là ước của , ta có thể loại bỏ tất cả các số chia hết cho khỏi danh sách xét duyệt. Khi kết hợp với giả thiết rằng là số lẻ, ta chỉ cần xét những số , từ đó giảm số lượng trường hợp cần kiểm tra xuống còn .
Ta hoàn toàn có thể mở rộng thêm với nhiều số nguyên tố hơn để tối ưu hóa hơn nữa việc tìm kiếm các ước số nguyên tố.
Để thuận tiện cho việc cài đặt, ta định nghĩa mảng để nhảy đến số "nghi ngờ là số nguyên tố" tiếp theo.
Ví dụ: Xét các modulo , , . Bỏ qua , các số nguyên cần duyệt phải thỏa mãn:
hay
Như vậy, ta có thể thiết lập các khoảng cách để nhảy đến các số cần duyệt tiếp theo là:
hay
Dưới đây là cài đặt cho ví dụ trên.
vector<long long> trial_division3(long long n) {
vector<long long> factorization;
for (int d : {2, 3, 5}) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
const int increments[] = {4, 2, 4, 2, 4, 6, 2, 6};
int i = 0;
for (long long d = 7; d * d <= n; d += increments[i++]) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
if (i == 8)
i = 0;
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
Mở rộng cho càng nhiều số nguyên tố thì thuật toán càng tốt hơn. Tuy nhiên mảng sẽ càng dài hơn trong khi tỷ lệ phần tử cần xét so với ban đầu cũng không giảm nhiều:
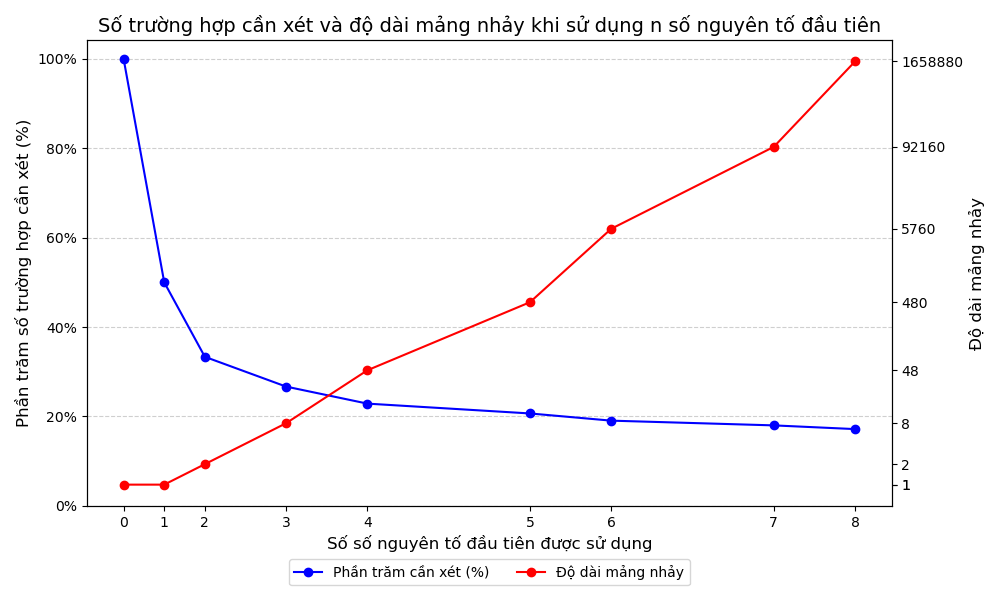
Thuật toán này cũng đã được đề cập đến trong bài viết về Sàng nguyên tố - VNOI.
¶ Sử dụng sàng nguyên tố
Sử dụng Sàng nguyên tố, ta chỉ cần duyệt các số nguyên tố trong . Từ đó, độ phức tạp cho việc phân tích mỗi lần giảm chỉ còn (do số lượng số nguyên tố nhỏ hơn xấp xỉ - theo Định lý số nguyên tố). Tuy nhiên, ta sẽ tốn thêm bộ nhớ lưu mảng và độ phức tạp thời gian của cài đặt sẽ cần tính thêm thời gian chuẩn bị sàng.
vector<long long> primes;
vector<pair<unsigned long long, int>> trial_division4(unsigned long long n){
vector<pair<unsigned long long, int>> result;
for (auto p: primes) {
if (p * p > n) break;
if (n % p) continue;
int cnt = 0;
while (n % p == 0) {
cnt++;
n /= p;
}
result.emplace_back(p, n);
}
return result;
}
¶ Thuật toán Pollard's Rho
Thuật toán Pollard's Rho sẽ giúp ta tìm một ước khác một của với độ phức tạp thời gian trung bình .
Do số nhân tử của tối đa là , toàn bộ thuật toán phân tích bằng thuật Pollard's Rho có độ phức tạp trung bình là là . Do thuật toán sử dụng yếu tố ngẫu nhiên, cài đặt sử dụng Pollard's Rho sẽ không có độ phức tạp chính xác.
Thuật toán có độ phức tạp không gian (Chỉ tốn duy nhất 1 mảng lưu kết quả).
¶ Ý tưởng lớn
-
Nếu là số nguyên tố thì ta không cần phân tích nữa. (Có thể kiểm tra bằng thuật toán Miller-Rabin với độ phức tạp ).
-
Nếu không là số nguyên tố.
Ta sẽ sinh một dãy và tìm hai chỉ số sao cho:Như vậy, ta tìm được là một ước của .
Nếu thì chúng ta cần lặp lại thuật toán với một dãy khác.
Tiếp tục tách và theo cách trên đến khi tách được hết các ước nguyên tố.Liệu có chắc chắn tồn tại s, t không?
Giả sử là một ước khác của . Theo nguyên lý Dirichlet, cho một dãy số có ít nhất phần tử, ta chắc chắn tìm được hai chỉ số thỏa hay .
Ta cũng quy ước .
Đến đây, chúng ta có ba vấn đề cần giải quyết:
Dãy cần ít nhất bao nhiêu phần tử để tồn tại hai chỉ số ?
Nghịch lý ngày sinh nhật
Làm sao để sinh dãy hiệu quả ?
Đề xuất của Pollard
Làm sao để tìm được nếu đã có dãy ?
Thuật toán phát hiện chu trình
Chúng ta sẽ giải quyết lần lượt ba vấn đề trên.
¶ 1. Nghịch lý ngày sinh nhật
Theo Nghịch lý ngày sinh nhật (Birthday paradox):
Trong một tập số nguyên chọn ra từ với , thì xác suất tồn tại hai số bằng nhau xấp xỉ .
Nếu chọn dãy khoảng phần tử thì từ dãy sẽ lấy được hai số bằng nhau với xác suất .
Giả sử ta đang cố gắng tìm một ước của thỏa mãn , thì số phần tử cần lấy xấp xỉ .
Như vậy, tiếp theo ta sẽ đến với cách để sinh ngẫu nhiên một dãy để lấy được khoảng phần tử này.
¶ 2. Đề xuất của Pollard
Pollard đã đề xuất sử dụng một hàm giả ngẫu nhiên để sinh dãy .
Định nghĩa hàm là
Ta sinh dãy như sau:
bất kỳ
Nhận xét: Với một số nguyên bất kỳ, theo nguyên lý Dirichlet, luôn tồn tại sao cho .
Khi đã tìm được , có 2 trường hợp xảy ra:
- TH1: thì ta đã tìm được một ước của . Chia liên tục cho ước này rồi sau đó, lặp lại thuật toán để tìm ước khác.
- TH2: thì ta sẽ lặp lại thuật toán với khác và/hoặc khác.
Để tránh gặp phải trường hợp TH2 quá nhiều, ta có thể xét trước các ước nguyên tố nhỏ như do các modulo nhỏ như vậy có xác suất cao gặp phải TH2.
Dưới đây là minh họa cho dãy với , , và . Đây cũng chính là lý do Pollard đặt tên cho Thuật toán của ông (Pollard's algorithm, theo Wikipedia).
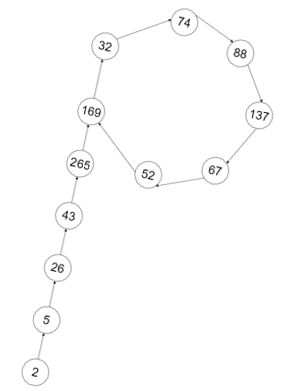
¶ 3. Thuật toán phát hiện chu trình
Qua hình minh họa trên, ta thấy rõ ràng rằng dãy là tuần hoàn.
Chứng minh
Khi đó hay .
Bằng phương pháp quy nạp, dễ thấy rằng dãy sẽ tuần hoàn theo chu kỳ .
Do đó, việc tìm hai số và cũng chính là xác định một chu kỳ của dãy số .
Cũng từ hình minh họa, ta có thể coi là một đỉnh của đồ thị và có cạnh có hướng đến đỉnh . Từ đó, bài toán được đưa về tìm chu trình của đồ thị này.
Xét là độ dài chu trình và là vị trí đầu tiên xuất hiện chu trình.
Dưới đây là hai thuật toán có Độ phức tạp thời gian và không gian .
¶ 3.1. Thuật toán rùa và thỏ (Thuật toán Floyd)
Thuật toán này rất đơn giản: Sử dụng hai con trỏ "Rùa" và "Thỏ". Mỗi lần "Rùa" sẽ nhảy bước, "Thỏ" sẽ nhảy bước.
Nếu "Thỏ" gặp "Rùa" thì đường chúng đã đi có chu trình. Nếu không tồn tại chu trình, "Thỏ" sẽ đến hết điểm hết đồ thị trước "Rùa".
Chứng minh thuật toán trên khả thi
- Nếu đồ thị không có chu trình, rõ ràng Thỏ luôn đi nhanh hơn Rùa và không bao giờ gặp được Rùa.
- Nếu đồ thị có chu trình độ dài , xét tại một thời điểm mà Thỏ ở trước Rùa bước trong chu trình.
Giả sử . Gọi vị trí của Rùa là , suy ra Thỏ ở vị trí . Sau khoảng thời gian , Rùa sẽ ở vị trí , còn Thỏ ở vị trí . Do đồ thị có chu trình dài bước nên Rùa và Thỏ đang ở cùng vị trí (đpcm).
¶ Mã giả tìm chu trình:
int Floyd(int x0){
int tortoise = f(x0);
int hare = f(f(x0));
while (tortoise != hare){
tortoise = f(tortoise);
hare = f(f(hare));
}
return hare;
}
ĐPT của Thuật toán Floyd là do sử dụng sau mỗi bước nhảy của Rùa và Thỏ.
Code C++ minh họa:
long long mult(long long a, long long b, long long mod) {
return (__int128_t)a * b % mod;
}
long long f(long long x, long long c, long long mod) {
return (mult(x, x, mod) + c) % mod;
}
long long rho(long long n, long long x0 = 2, long long c = 1) {
long long tortoise = x0;
long long hare = x0;
long long g = 1;
while (g == 1) {
tortoise = f(tortoise, c, n);
hare = f(hare, c, n);
hare = f(hare, c, n);
g = gcd(abs(tortoise - hare), n);
}
return g;
}
Chú ý rằng, không phải kỳ thi nào cũng có thể sử dụng __int128_t (do máy chấm) nên có thể sử dụng hàm mult thay thế sau (nhân Ấn Độ với độ phức tạp ):
long long mult(long long a, long long b, long long mod){
if (!b) return 0;
long long x = mult(a, b / 2);
if (b % 2 == 0)
return 2 * x % mod;
else
return (2 * x + a) % mod;
}
Minh họa cho , và :
Bảng minh họa cho Thuật toán Floyd trong trường hợp trên:
| Step | Rua | Tho | |
|---|---|---|---|
| - | |||
Như vậy, sau Step 7, ta kết luận được là một ước của
¶ 3.2. Thuật toán Brent
Năm , Brent đã cải tiến Thuật toán Rho tìm ước bằng cách sử dụng một cách tìm chu trình khác (tạm gọi là Thuật toán Brent).
Gọi là độ dài chu trình và là vị trí đầu tiên xuất hiện chu trình. Vẫn ý tưởng sử dụng hai con trỏ, nhưng ta sẽ tìm nhỏ nhất mà lớn hơn cả và .
Sau đó, ta sẽ tìm bằng cách cho và tìm vị trí sao cho .
Minh họa cho , và :
Mô tả:
Duyệt từ :
- Cho Rùa chạy đến
- Cho Thỏ chạy từ đến xem có tồn tại giá trị bằng Rùa không. Nếu tồn tại thì kết thúc thuật toán.
Mã giả tìm chu trình:
int f(int x, int c = 1){
return x * x + c;
}
int Brent(int x0){
int tortoise = x0;
int hare = f(x0);
int power = 1;
while (tortoise != hare){
tortoise = hare;
for (int i = 1; i <= power; ++i){
hare = f(hare);
if (tortoise == hare){
break;
}
}
power *= 2;
}
return hare;
}
Để tăng tốc thuật toán, chúng ta có các nhận xét:
- Không cần xét các vị trí
Loại được khoảng 50% số trường hợp
Chứng minh
Khi duyệt đến , cho Rùa đứng ở vị trí . Xét việc bỏ qua các giá trị mà .
- Nếu không bị bỏ qua, ta có đpcm.
- Nếu bị bỏ qua thì suy ra và suy ra . Nếu thì ... Cứ tiếp tục làm như vậy nào đó để và thì chốt lại ta có . Như vậy khi duyệt đến , ta chắc chắn tìm được vị trí của thỏ (đpcm).
- Nếu thì chắc chắn một trong các số sẽ thỏa mãn (dễ dàng chứng minh bằng phản chứng).
- Để so sánh, trong thuật toán gốc, ta gọi theo mỗi bước Thỏ chạy, tức là vào khoảng lần. Xét hai trường hợp sau:
- Nếu thì chính là một ước cần tìm của .
Cả thuật toán gọi khoảng lần. - Nếu , ta cần một lần duyệt bước để tìm vị trí Thỏ gặp Rùa và tính mỗi bước.
Cả thuật toán gọi khoảng lần.
- Nếu thì chính là một ước cần tìm của .
- Chú ý: Để tích không quá to, ta sử dụng
- Để so sánh, trong thuật toán gốc, ta gọi theo mỗi bước Thỏ chạy, tức là vào khoảng lần. Xét hai trường hợp sau:
Độ phức tạp thời gian của Thuật toán Brent vẫn là .
Tuy nhiên, Thuật toán Brent lại có số lần sử dụng ít hơn Thuật toán Floyd rất nhiều nên đã tăng tốc thuật toán tìm chu trình khoảng và thuật toán phân tích số nguyên khoảng - theo Brent.
Code C++ minh họa
// CP- Algorithms
long long brent(long long n, long long x0 = 2, long long c = 1) {
long long tortoise = x0;
long long g = 1;
long long q = 1;
long long hare, xs;
int m = 128;
int l = 1;
while (g == 1) {
hare = tortoise;
for (int i = 1; i < l; i++)
tortoise = f(tortoise, c, n);
int k = 0;
while (k < l && g == 1) {
xs = tortoise;
for (int i = 0; i < m && i < l - k; i++) {
tortoise = f(tortoise, c, n);
q = mult(q, abs(hare - tortoise), n);
}
g = gcd(q, n);
k += m;
}
l *= 2;
}
if (g == n) {
do {
xs = f(xs, c, n);
g = gcd(abs(xs - hare), n);
} while (g == 1);
}
return g;
}
`
Bảng dưới đây là minh họa cho thuật toán Brent với , và .
Dãy số: Ở bước , ta không xét do
| - | |||||
| , | |||||
¶ Code C++ phân tích thừa số nguyên tố tham khảo
Dưới đây là code được tham khảo từ RR Code. Code đã xét trước các nhân tử trước khi sử dụng Thuật toán Pollard's Rho với cải tiến của Brent.
Như đã nói ở trên, dưới đây là ước lượng độ phức tạp của thuật toán:
- Thời gian trung bình: .
- Không gian: (để lưu kết quả phân tích).
Code đã vượt qua test với trong khoảng tại Library Checker - Factorize.
Code C++ minh họa
#include <bits/stdc++.h>
using namespace std;
// Copied from
// https://github.com/ngthanhtrung23/ACM_Notebook_new/blob/master/Math/NumberTheory/Pollard_factorize.h
using ll = long long;
using ull = unsigned long long;
using ld = long double;
// Dưới đây là hàm mult nhanh gấp đôi sử dụng __int128_t
/* License: CC0
* Source: https://github.com/RamchandraApte/OmniTemplate/blob/master/src/number_theory/modulo.hpp
* Description: Calculate $a\cdot b\bmod c$ (or $a^b \bmod c$) for $0 \le a, b \le c \le 7.2\cdot 10^{18}$.
* Time: O(1) for \texttt{modmul}, O(\log b) for \texttt{modpow}
* Status: stress-tested, proven correct
* Details:
* This runs ~2x faster than the naive (__int128_t)a * b % M.
* A proof of correctness is in doc/modmul-proof.tex. An earlier version of the proof,
* from when the code used a * b / (long double)M, is in doc/modmul-proof.md.
* The proof assumes that long doubles are implemented as x87 80-bit floats; if they
* are 64-bit, as on e.g. MSVC, the implementation is only valid for
* $0 \le a, b \le c < 2^{52} \approx 4.5 \cdot 10^{15}$.
*/
ll mult(ll x, ll y, ll md) {
ull q = (ld)x * y / md;
ll res = ((ull)x * y - q * md);
if (res >= md) res -= md;
if (res < 0) res += md;
return res;
}
// Hàm tính lũy thừa nhanh
ll powMod(ll x, ll p, ll md) {
if (p == 0) return 1;
if (p & 1) return mult(x, powMod(x, p - 1, md), md);
return powMod(mult(x, x, md), p / 2, md);
}
// Thuật toán Rabin Miller hỗ trợ kiểm tra các số nguyên tố lớn
bool checkMillerRabin(ll x, ll md, ll s, int k) {
x = powMod(x, s, md);
if (x == 1) return true;
while (k--) {
if (x == md - 1) return true;
x = mult(x, x, md);
if (x == 1) return false;
}
return false;
}
// Hàm kiểm tra nhanh một số có nguyên tố hay không
bool isPrime(ll x) {
if (x == 2 || x == 3 || x == 5 || x == 7) return true;
if (x % 2 == 0 || x % 3 == 0 || x % 5 == 0 || x % 7 == 0) return false;
if (x < 121) return x > 1;
ll s = x - 1;
int k = 0;
while (s % 2 == 0) {
s >>= 1;
k++;
}
if (x < 1LL << 32) {
for (ll z : {2, 7, 61}) {
if (!checkMillerRabin(z, x, s, k)) return false;
}
} else {
for (ll z : {2, 325, 9375, 28178, 450775, 9780504, 1795265022}) {
if (!checkMillerRabin(z, x, s, k)) return false;
}
}
return true;
}
ll gcd(ll x, ll y) { return y == 0 ? x : gcd(y, x % y); }
mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count());
long long get_rand(long long r) {
return uniform_int_distribution<long long>(0, r - 1)(rng);
}
void pollard(ll x, vector<ll> &ans) {
if (isPrime(x)) {
ans.push_back(x);
return;
}
ll c = 1;
while (true) {
// Định nghĩa hàm f sử dụng cú pháp lambda function
c = 1 + get_rand(x - 1);
auto f = [&](ll y) {
ll res = mult(y, y, x) + c;
if (res >= x) res -= x;
return res;
};
ll y = 2;
int B = 100;
int len = 1;
ll g = 1;
// Sử dụng thuật cải tiến của Brent ở đây
while (g == 1) {
ll z = y;
for (int i = 0; i < len; i++) {
z = f(z);
}
ll zs = -1;
int lft = len;
while (g == 1 && lft > 0) {
zs = z;
ll p = 1;
for (int i = 0; i < B && i < lft; i++) {
p = mult(p, abs(z - y), x);
z = f(z);
}
g = gcd(p, x);
lft -= B;
}
if (g == 1) {
y = z;
len <<= 1;
continue;
}
if (g == x) {
g = 1;
z = zs;
while (g == 1) {
g = gcd(abs(z - y), x);
z = f(z);
}
}
if (g == x) break;
assert(g != 1);
// Thay vì kết thúc như thuật toán Brent,
// tiếp tục phân tích hai phần g và x / g
pollard(g, ans);
pollard(x / g, ans);
return;
}
}
}
// return list of all prime factors of x (can have duplicates)
vector<ll> factorize(ll x) {
vector<ll> ans;
for (ll p : {2, 3, 5, 7, 11, 13, 17, 19}) {
while (x % p == 0) {
x /= p;
ans.push_back(p);
}
}
if (x != 1) {
pollard(x, ans);
}
sort(ans.begin(), ans.end());
return ans;
}
// return pairs of (p, k) where x = product(p^k)
vector<pair<ll, int>> factorize_pk(ll x) {
auto ps = factorize(x);
ll last = -1, cnt = 0;
vector<pair<ll, int>> res;
for (auto p : ps) {
if (p == last)
++cnt;
else {
if (last > 0) res.emplace_back(last, cnt);
last = p;
cnt = 1;
}
}
if (cnt > 0) {
res.emplace_back(last, cnt);
}
return res;
}
¶ Các thuật toán khác
Phân tích thừa số nguyên tố là một bài toán quan trọng trong khoa học máy tính và đã có rất nhiều thuật toán cải tiến cho bài toán này.
Trong từng trường hợp, các thuật toán phân tích nhân tử (PTNT) có thể kể đến như sau:
Dưới đây là bảng đã tách riêng cột ĐPT:
| Bộ dữ liệu (N) | ||
|---|---|---|
PTNT sử dụng các sàng nguyên tố. |
hoặc tùy cách cài đặt. | |
★ Thuật toán Pollard's Rho (Pollard's Rho algorithm). |
cho cả hai thuật toán, nhưng Pollard's Rho thường được sử dụng phổ biến hơn do dễ cài đặt hơn. | |
| Thuật toán PTNT đường cong elliptic Lenstra (Lenstra elliptic-curve factorization) (ECM) | , với là các ước nguyên tố của . | |
| Thuật toán sàng bậc hai (Quadratic Sieve) (QS) | , với là các ước nguyên tố của . | |
| Lớn hơn | Sàng trường số tổng quát (General number field Sieve) (GNFS) | . |
* Về độ phức tạp hay trong ký hiệu L-notation là :
- là một hằng số.
- Còn hay :
với