¶ Matroid
-
Tác giả:
- Đặng Đoàn Đức Trung - UT Austin
-
Reviewer:
- Trần Xuân Bách - University of Chicago
¶ Giới thiệu
Mục đích của bài viết này là để giới thiệu với các bạn đọc về matroid, vốn là một cấu trúc trong đại số trừu tượng nhưng lại được sử dụng ở một số bài nâng cao trong lập trình thi đấu. Bài viết này sẽ chỉ giới thiệu về định nghĩa của matroid, cùng với một số tính chất đặc biệt của matroid giúp việc xây dựng các thuật toán tham lam trên matroid trở nên dễ hơn rất nhiều so với các bài khác không có matroid.
Bài viết này là phần 1 của chuỗi bài viết về các thuật toán liên quan tới matroid.
¶ Lưu ý trước khi đọc
Bài viết này cần người đọc vững về các toán tử trên tập hợp, ví dụ như phép giao , phép hợp , phép hiệu , toán tử tập con và , v.v.
Mình sẽ dùng kí hiệu cho việc thêm một phần tử vào tập, và cho việc loại một phần tử khỏi tập.
¶ Một số ví dụ xây dựng
Với các bạn đã làm một số bài về xor basis, với một tập gồm các số tự nhiên, ta có một số định nghĩa sau đây. Với một tập con bất kì:
- được gọi là tập độc lập (independent set) nếu không có bất kì tập con không rỗng nào của mà tổng xor của tập con này bằng .
- được gọi là cơ sở (basis) của nếu với mọi phần tử thuộc , không còn là tập độc lập. Nói cách khác, cơ sở có thể được coi như là một tập độc lập cực đại, khi thêm bất kì phần tử nào vào sẽ làm tập mất tính độc lập.
Ở đây, khái niệm độc lập được định nghĩa dựa trên việc tồn tại một tập con các phần tử có tổng xor bằng . Tuy nhiên, ta không nhất thiết phải ép buộc vào một định nghĩa của độc lập như thế.
Xét ví dụ sau: cho đồ thị vô hướng liên thông gồm đỉnh và cạnh. Gọi tập tất cả các cạnh trên là tập . Ta có thể dựng một định nghĩa về tập độc lập của như sau. Với một tập con bất kì:
- được gọi là tập độc lập nếu các cạnh trong không dựng nên bất kì chu trình nào.
- được gọi là cơ sở với định nghĩa y hệt như trường hợp trên: không tồn tại cạnh nào thuộc sao cho là tập độc lập.
Ta dễ dàng nhận ra được là dưới định nghĩa tập độc lập như trên, nếu tập là cở sở của , các cạnh trong dựng nên một cây khung của đồ thị . Nói cách khác, các cây khung của dựng nên các cơ sở cho định nghĩa tập độc lập như trên. Đây là một cách định nghĩa tập độc lập trên tập các cạnh của đồ thị khá hữu ích.
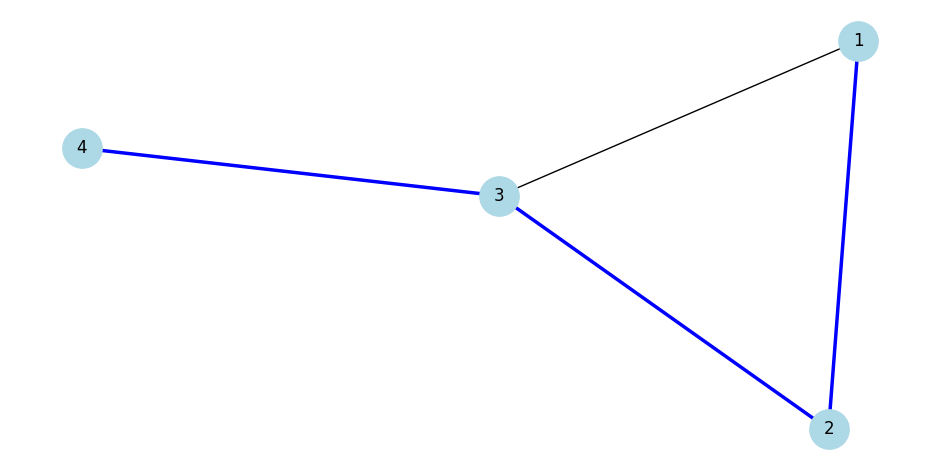 |
|---|
| Một tập cạnh độc lập. Đây còn là một cơ sở. |
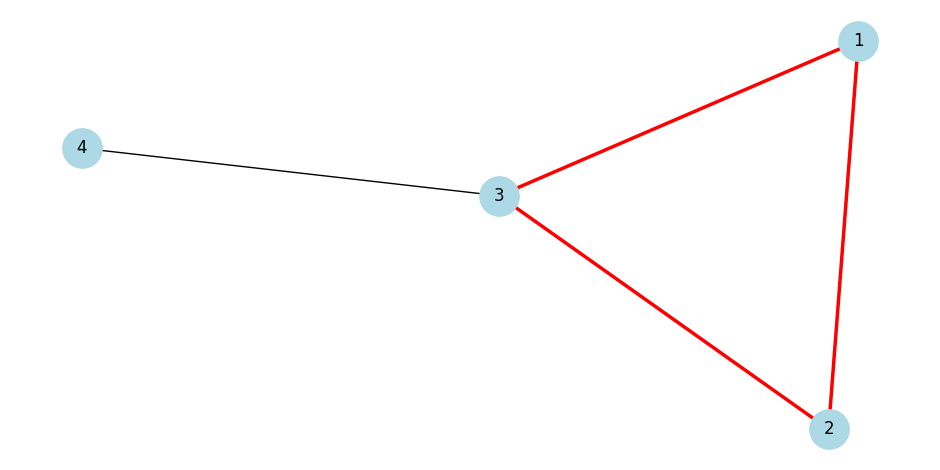 |
|---|
| Một tập cạnh không độc lập. |
Matroid là một cách tổng quát hóa định nghĩa độc lập cho bất kì tập hữu hạn nhằm giữ lại các tính chất tốt của các định nghĩa tập độc lập như xor basis hay cây khung. Mặc dù định nghĩa mình giới thiệu sau đây có thể nghe trừu tượng, định nghĩa này có thể bao quát rất nhiều cấu trúc quan trọng trong lập trình thi đấu.
¶ Định nghĩa, các ví dụ điển hình, và một số tính chất của matroid
Với một tập hữu hạn (tập này còn được gọi là ground set), giả sử ta định nghĩa một tính chất độc lập trên , và ta thu được là tập hợp của các tập độc lập của . Khi này (hay nói đúng hơn là cặp ) là một matroid khi:
- Tập rỗng là tập độc lập: .
- Nếu tập con là tập độc lập thì tập con của cũng là tập độc lập. Nói cách khác, nếu thỏa mãn thì cũng thỏa mãn .
- Nếu tập độc lập có nhiều phần tử hơn tập độc lập , ta có thể tìm phần tử thuộc mà không thuộc mà có thể thêm vào và vẫn làm cho độc lập. Nói cách khác, nếu và , tồn tại sao cho .
Để làm định nghĩa tường minh hơn, ta quay lại về ví dụ của tập độc lập trên các cạnh của đồ thị như trên.
- Định nghĩa tập là tập các cạnh trên .
- Định nghĩa tập là tập của tập con các cạnh thuộc sao cho không tồn tại chu trình trong tập con các cạnh được chọn. Nói cách khác, một tập con các cạnh là tập độc lập nếu các cạnh này không tạo ra chu trình.
Ta có thể chứng minh được rằng là một matroid như sau:
- Rõ ràng tập rỗng là tập độc lập: nếu không có cạnh nào thì không có chu trình.
- Nếu một tập là tập độc lập thì các tập con của cũng là tập độc lập, vì nếu không chứa chu trình nào thì tập con của cũng vậy.
- Nếu tập cạnh và là hai tập độc lập (không chứa chu trình), và nếu , ta có thể tìm được cạnh trong và đặt vào sao cho vẫn không có chu trình. Mình xin được dành phần này cho bạn đọc tự chứng minh.
¶ Một số matroid điển hình
Một số matroid điển hình bao gồm:
- Matroid đồ thị (graphic matroid). Cho một đồ thị vô hướng. Định nghĩa tập là tập cạnh của , và một tập con của là tập độc lập nếu cạnh trong tập con này không tạo thành chu trình. Đây là matroid ta vừa nêu ở ví dụ làm rõ trên.
- Matroid đồng nhất (uniform matroid). Cho một tập gồm phần tử hữu hạn bất kì, và một số nguyên không âm . Nếu ta định nghĩa tập con của là tập độc lập nếu tập con này chứa không quá phần tử, thì đây là matroid đồng nhất hạng .
- Matroid đa sắc (colorful matroid). Cho một tập gồm phần tử, mỗi phần tử có một màu . Nếu ta định nghĩa tập con của là tập độc lập nếu như không có màu nào được lặp lại trong tập con, thì đây là matroid đa sắc.
- Matroid tuyến tính (linear/vector matroid). Cho một tập gồm véctơ trên một trường đại số bất kì. Với định nghĩa tập độc lập là các tập con của độc lập trên trường đại số đã cho, thì ta thu được matroid tuyến tính. Xor basis là điển hình của matroid tuyến tính, với trường đại số ở đây là .
- Matroid đoạn hoành (transversal matroid). Cho đồ thị hai phía , với tập là tập các đỉnh ở phía trái đồ thị. Ta định nghĩa tập con các đỉnh của là tập độc lập nếu tồn tại một cách ghép tất cả các đỉnh của tập con này với các đỉnh ở phía phải đồ thị. Dưới định nghĩa này, ta thu được matroid đoạn hoành.
¶ Một số tính chất của matroid
Với tập con , ta định nghĩa hạng của () là kích cỡ tập con độc lập to nhất của , thì ta thu được một số tính chất sau về hạng của :
- Hạng của không quá kích cỡ của : \rank(U) \le |U|.
- Nếu là tập độc lập, thì hạng của chính bằng kích cỡ của : U \in \mathcal{I} \Leftrightarrow \rank(U) = |U|.
- Hàm \rank thỏa mãn tính chất môđun thứ (submodular): với , ta có \rank(U) + \rank(V) \ge \rank(U \cup V) + \rank(U \cap V).
Ta có thể định nghĩa thêm hạng của toàn bộ matroid là hạng của toàn bộ tập (r = \rank(E)), và cơ sở là các tập độc lập tối đa của matroid (ta không thể thêm phần tử nào khác vào mà vẫn giữ tập được độc lập), thì ta có tính chất sau:
- Cơ sở của matroid là các tập độc lập mà |U| = \rank(U) = r.
- Với hai cơ sở khác nhau và , và với mọi , ta có thể tìm được sao cho vẫn là một cơ sở. Đây được gọi là tính chất trao đổi cơ sở (basis exchange property) của một matroid.
¶ Thuật toán tham lam tìm cơ sở nhỏ nhất/lớn nhất
Xét bài toán sau:
Cho matroid định nghĩa trên tập có phần tử, sao cho mỗi phần tử trong tập có một trọng số . Hãy tìm cơ sở của matroid có tổng trọng số lớn nhất/nhỏ nhất.
Không mất tính tổng quát, ta sẽ giải bài toán tìm cơ sở lớn nhất. Ta có thuật toán tham lam sau để tìm cơ sở lớn nhất của matroid.
- Sắp xếp các phần tử của theo trọng số giảm dần.
- Bắt đầu bằng tập .
- Ta lặp qua các phần tử của sau khi đã sắp xếp. Với phần tử hiện tại, nếu vẫn còn là tập độc lập, ta thêm vào (gán .)
- Sau khi lặp, ta trả lại .
Ta có thể chứng minh được thuật toán này trả về cơ sở lớn nhất của matroid. Ngoài ra, giả sử ta được cho một hàm kiểm tra tính độc lập: với tập độc lập và phần tử bất kì, ta có thể kiểm tra nếu là tập độc lập trong độ phức tạp , thì thấy rằng độ phức tạp của thuật toán trên là .
Chứng minh thuật toán
Giả sử thuật toán trả về cơ sở . Xét bất kì cơ sở nào khác , và giả sử là ta đã sắp xếp và theo thứ tự trọng số giảm dần, tức là và .
Với mọi từ tới , xét và . Vì và là tập độc lập, ta có và cũng là tập độc lập (tiên đề 2 của matroid). Ngoài ra, vì , theo tiên đề 3 của matroid, tồn tại phần tử nào đó của có thể cho vào để vẫn là tập độc lập (với ). Tuy nhiên, theo thuật toán trên, là phần tử có trọng số lớn nhất có thể cho vào để tập vẫn độc lập. Vậy nên ta có . Vì ta chứng minh được điều này đúng với mọi , ta có .
Với bài toán tìm cơ sở nhỏ nhất, ta chỉ cần đổi thứ tự sắp xếp của .
Cuối cùng, ta nhận thấy rằng với trường hợp đặc biệt của matroid đồ thị, thuật toán trên chính là thuật toán Kruskal để tìm cây khung lớn nhất, vì cây khung là cơ sở của matroid đồ thị.
¶ Cài đặt mẫu
Dưới đây là cách cài đặt tìm cơ sở lớn nhất, cùng với cách áp dụng vào bài toán tìm cây khung lớn nhất.
#include <bits/stdc++.h>
using namespace std;
struct DSU {
vector<int> par;
DSU(int n) : par(n, -1) {}
int comp(int u) { return par[u] < 0 ? u : par[u] = comp(par[u]); }
bool connect(int u, int v) {
if ((u = comp(u)) == (v = comp(v))) {
return false;
}
if (par[u] > par[v]) {
swap(u, v);
}
par[u] += par[v]; par[v] = u;
return true;
}
};
struct GraphMat {
vector<pair<int, int>> edges;
int n;
DSU d;
GraphMat(int n, vector<pair<int, int>> edges) : n(n), d(n), edges(edges) {}
bool check(int x) {
// kiểm tra nếu ta có thể thêm phần tử a vào tập S hiện tại
auto [u, v] = edges[x];
return d.comp(u) != d.comp(v);
}
void add(int x) {
// thêm a vào tập S hiện tại
auto [u, v] = edges[x];
d.connect(u, v);
}
void clear() { d = DSU(n); }
};
template<class M>
vector<int> largestBasis(M mat, int n, vector<int> w) {
vector<int> elem(n);
iota(elem.begin(), elem.end(), 0);
sort(elem.begin(), elem.end(), [&](int u, int v) { return w[u] > w[v]; });
vector<int> S = {};
for (int u : elem) {
if (mat.check(u)) {
S.push_back(u);
mat.add(u);
}
}
return S;
}
int main() {
// tìm cây khung lớn nhất
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<pair<int, int>> edges;
vector<int> w(m);
for (int i = 0; i < m; i++) {
int u, v; cin >> u >> v >> w[i]; u--; v--; // giả sử đồ thị cho đỉnh từ 1 tới n, ta biến thành từ 0 tới n - 1
edges.push_back({u, v});
}
GraphMat mat(n, edges);
vector<int> span = largestBasis(mat, m, w);
for (auto x : span) {
auto [u, v] = edges[x];
cout << u + 1 << " " << v + 1 << "\n";
}
}