¶ Căn bậc 2 modulo
Người viết:
- Nguyễn Minh Hiển - Trường Đại học Công nghệ, ĐHQGHN
Reviewer:
- Phạm Công Minh - Trường Đại học Công nghệ, ĐHQGHN
Đôi khi, chúng ta sẽ gặp những bài tập như tính hay thậm chí như tính số Fibonacci . Mà chúng ta biết, công thức tổng quát:
Việc xuất hiện đặt ra nhiều thách thức cho việc tính toán nhanh , nhưng đồng thời cũng mở ra những phương pháp mới để chinh phục được bài toán
¶ Một số định nghĩa
- Số nguyên dương được gọi là thặng dư bình phương modulo nếu:
Khi này, được gọi là căn bậc hai của modulo .
- Ký hiệu Legendre: với là số nguyên tố lẻ
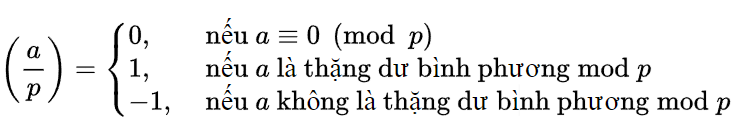
¶ Kiểm tra thặng dư bình phương
Ta sử dụng tiêu chuẩn Euler (Euler's criterion) như sau. Với nguyên tố lẻ:
Đến đây, ta sử dụng lũy thừa nhanh để tính.
int pow_mod(int a, int n, int p); // hàm tính lũy thừa nhanh modulo p
int legendre_symbol(int a, int p) {
return pow_mod(a, (p - 1) >> 1, p);
}
Độ phức tạp:
¶ Thặng dư bình phương modulo nguyên tố
¶ Bài toán
VNOJ - Số học 1
Tìm tất cả thỏa mãn phương trình:
- Với , phương trình có đúng nghiệm:
- Với lẻ, theo định lý Lagrange, phương trình có đúng nghiệm
Như vậy, ta sẽ tìm nghiệm trong trường hợp lẻ.
¶ Tìm thặng dư không chính phương bất kỳ
- Trước hết, ta cần tìm thặng dư "không chính phương" để thực hiện hai thuật toán bên dưới.
- Vì một nửa số phần tử trong tập là thặng dư không chính phương, nên ta sẽ duyệt từng số từ cho đến khi gặp được số thỏa mãn. Để kiểm tra một số thỏa mãn hay không, ta sử dụng cách Tiêu chuẩn Euler bên trên.
- Để thuật toán hiệu quả hơn, bạn nên sinh số ngẫu nhiên và kiểm tra đến khi tìm được. Xác suất lần thử tìm được là , nên xác suất sau lần thử mà bạn chưa tìm ra là .
¶ Thuật toán Tonelli-Shanks
- Thuật toán:
- Bài viết xin không đề cập phần chứng minh thuật toán. Bạn đọc tham khảo tại Wikipedia.
- Bước 1: ta phân tích với lẻ
- Bước 2: Chọn là một thặng dư không chính phương bất kỳ.
- Bước 3: Gán
- Bước 4: Lặp
- Tìm nhỏ nhất sao cho
- Nếu thì chính là đáp án cần tìm.
Nếu thì đặt gán:
- Code C++ minh họa:
int pow_mod(long long a, long long k, long long M) {
long long ans = 1;
for (; k > 0; a = a * a % M, k >>= 1) {
if (k & 1) {
ans = ans * a % M;
}
}
return ans;
}
int Tonelli_Shanks(int a, int p) {
if (p == 2) {
return (a & 1);
}
int S = 0, Q = p - 1;
while (Q % 2 == 0) {
S++;
Q /= 2;
}
int z = 2;
while (legendre_symbol(z, p) != p - 1) {
z++;
}
int x = pow_mod(a, (Q + 1) >> 1, p), b = pow_mod(a, Q, p);
int m, v, e, u;
while (b % p != 1) {
m = 0, v = 1; // v = 2^m
while (pow_mod(b, v, p) != 1) {
m++;
v <<= 1;
}
e = Q << (S - m - 1);
u = pow_mod(z, e, p);
x = (1LL * x * u) % p;
b = (((1LL * u * u) % p) * b) % p;
}
return x;
}
- Độ phức tạp:
¶ Trường hữu hạn
¶ Định nghĩa
- Như các bạn đã biết:
Trong đó và .
Bạn đọc có thể thấy nó khá giống số phức, chỉ thay bằng mà thôi.
Mục đích của chúng ta là tính theo . Như các bạn nghĩ đến, chúng ta sẽ sử dụng phép lũy thừa nhanh và có chút thay đổi cho phù hợp bài toán:
- Ký hiệu:
- Phần tử đơn vị:
- Xét phép nhân số
- Phép lũy thừa:
Các phép toán trên chỉ là một số tính chất của trường hữu hạn . Để có kiến thức đầy đủ hơn, bạn đọc tham khảo trên Wikipedia.
¶ Thuật toán Cipolla
- Thuật toán:
- Bài viết xin không đề cập phần chứng minh thuật toán. Bạn đọc tham khảo tại Wikipedia.
- Bước 1: Tìm sao cho là thặng dư không chính phương modulo
- Bước 2: Ta tính .
Khi đó, tìm được chính là nghiệm của bài toán.
Nói cách khác là trên
- Code C++ minh họa
Về cài đặt, như đã nói ở trên, khá giống số phức nên việc cài đặt cũng tương tự như vậy.
int a, p;
int k; // thặng dư không chính phương mod p
struct Complex {
int re, im;
Complex(int a = 0, int b = 0) {
re = a;
im = b;
}
Complex operator*(const Complex &o) {
Complex res;
res.re = (1LL * re * o.re + (1LL * im * k % p) * o.im) % p;
res.im = (1LL * re * o.im + 1LL * im * o.re) % p;
return res;
}
Complex pow(long long k) {
Complex res = Complex(1, 0), A = *this;
while (k) {
if (k & 1) res = res * A;
A = A * A;
k >>= 1;
}
return res;
}
};
int Cipolla(long long a, long long p) {
if (p == 2) {
return (a & 1);
}
// Tìm k = b^2 - a, sao cho k không chính phương
int b = 2;
while (true) {
b %= p;
k = (b * b - a) % p;
if (k < 0) k += p;
if (legendre_symbol(k, p) == p - 1) break;
b++;
}
// Ta cần tìm <b, 1>^((p+1)/2)
return Complex(b, 1).pow((p + 1) >> 1).re;
}
- Độ phức tạp:
¶ Fibonacci modulo p
Ngoài các phương pháp như Nhân ma trận hay Khử nhân ma trận, còn có một phương pháp khác sử dụng
Công thức tổng quát của Fibonacci:
Xét modulo nguyên tố.
- Nếu là thặng dư bình phương modulo
Ví dụ: Bài Codeforces - DZY Loves Fibonacci Numbers với .
Ta tính được:
Sử dụng nghịch đảo modulo, ta có:
So với việc tính lũy thừa của ma trận, tính lũy thừa của 2 số vẫn nhanh hơn rất nhiều.
- Nếu không là thặng dư bình phương modulo
Ví dụ: Bài VNOI - Fibonacci với
Ở bài này, ta sử dụng trường hữu hạn như ở trên.
Ta sẽ viết và
Trên thực tế, vì nguyên nên . Từ đó suy ra .
Do sử dụng công thức tổng quát, cách này có một ưu điểm mà không cách nào có được, thể hiện qua bài toán bên dưới đây.
Ví dụ: Bài F - ICPC miền Nam 2023
Tính theo modulo nguyên tố với:
Giới hạn: .
Lời giải
Xét:
với
Ta viết lại như sau:
Đặt , ta có:
Và
Bây giờ, chúng ta cần giải quyết bài toán tính nếu .
Chú ý rằng và có thể âm.
-
Cách 1: Trường hữu hạn
Ta có
Nếu thì
Thay , ta có ngay: -
Cách 2: Nhân liên hợp
Rõ ràng cách thứ hai này cho hiệu suất tốt hơn với khoảng trong khi cách thứ nhất sử dụng tới phép nhân.
Cả hai cách này đều có độ phức tạp tiệm cận , đủ để đánh bại bài toán này.
Code C++ tham khảo:
#include <bits/stdc++.h>
using namespace std;
const int MOD = 998244353;
const int inv = (MOD + 1) >> 1;
const int MAX = 1e6;
int fact[MAX + 5], ifact[MAX + 5];
long long N, K;
int pow_mod(long long A, long long k) {
long long res = 1;
while (k) {
if (k & 1) res = res * A % MOD;
A = A * A % MOD;
k >>= 1;
}
return res;
}
void add(int &x, const int &y) {
x += y;
if (x >= MOD) x -= MOD;
}
struct Complex {
int re, im;
Complex(int a = 0, int b = 0) {
re = a;
im = b;
}
bool operator==(const Complex &o) { return re == o.re && im == o.im; }
Complex operator+(const Complex &o) {
Complex res = *this;
add(res.re, o.re);
add(res.im, o.im);
return res;
}
Complex operator-(const Complex &o) {
Complex res = *this;
add(res.re, MOD - o.re);
add(res.im, MOD - o.im);
return res;
}
Complex operator*(const Complex &o) {
Complex res;
res.re = (1LL * re * o.re + 5LL * im * o.im) % MOD;
res.im = (1LL * re * o.im + 1LL * im * o.re) % MOD;
return res;
}
Complex operator*(int k) {
return Complex(1LL * re * k % MOD, 1LL * im * k % MOD);
}
Complex pow(long long k) {
if (k < 0) return this->pow(-k).inv();
Complex res = Complex(1, 0), A = *this;
while (k) {
if (k & 1) res = res * A;
A = A * A;
k >>= 1;
}
return res;
}
Complex inv() {
return Complex(re, MOD - im) *
pow_mod((1LL * re * re + 5LL * (MOD - im) * im) % MOD, MOD - 2);
}
Complex operator-() { return Complex(MOD - re, MOD - im); }
};
const Complex unit = Complex(1, 0);
void factorial() {
fact[0] = 1;
for (int i = 1; i <= MAX; ++i) fact[i] = 1LL * fact[i - 1] * i % MOD;
ifact[MAX] = pow_mod(fact[MAX], MOD - 2);
for (int i = MAX; i >= 1; --i) ifact[i - 1] = 1LL * ifact[i] * i % MOD;
}
int C(int n, int k, int p) {
return (1LL * fact[n] * ifact[k] % p) * ifact[n - k] % p;
}
int main() {
cin.tie(NULL)->sync_with_stdio(false);
factorial();
cin >> N >> K;
Complex res;
for (int i = 0; i <= K; ++i) {
Complex V1 = Complex(inv, inv).pow(2 * i - K);
if ((K - i) & 1) V1 = -V1;
Complex V2;
if (V1 == unit)
V2 = Complex((N + 1) % MOD, 0);
else {
V2 = V1.pow(N + 1);
V2 = (V2 - unit) * (V1 - unit).inv();
}
V2 = V2 * C(K, i, MOD);
if ((K - i) & 1)
res = res - V2;
else
res = res + V2;
}
if (K & 1)
cout << 1LL * res.im * pow_mod(5, MOD - 1 - K / 2) % MOD;
else
cout << 1LL * res.re * pow_mod(5, MOD - 1 - K / 2) % MOD;
}
¶ Bài tập luyện tập
❥ VNOI - Số học 1
❥ VNOI - Số học 2
❥ Codeforces - Div.1C - DZY Loves Fibonacci Numbers
❥ Codeforces - Mathematical Field of Experiments
❥ Codeforces - G - New Year and the Factorisation Collaboration
❥ Codechef - FN
❥ Codechef - LCASQRT
❥ Codechef - GUESSPRM
❥ Bài F - ICPC miền Nam 2023
¶ Tài liệu tham khảo
- Wikipedia:
- https://en.wikipedia.org/wiki/Quadratic_residue
- https://en.wikipedia.org/wiki/Euler's_criterion
- https://vi.wikipedia.org/wiki/Ký_hiệu_Legendre
- https://vi.wikipedia.org/wiki/Ký_hiệu_Jacobi
- https://en.wikipedia.org/wiki/Tonelli–Shanks_algorithm
- https://vi.wikipedia.org/wiki/Trường_hữu_hạn
- https://en.wikipedia.org/wiki/Cipolla's_algorithm
- https://en.wikipedia.org/wiki/Hensel's_lemma
- https://en.wikipedia.org/wiki/Lagrange's_theorem_(number_theory)