¶ Local Search
Tác giả: Nguyễn Thành Trung (RR)
¶ Bài toán mở đầu (TSP)
Cho N điểm trên mặt phẳng, đánh số từ 1 đến N. Tìm một chu trình xuất phát từ điểm thứ 1, đi qua tất cả các điểm, mỗi đỉnh đúng 1 lần và quay trở về đỉnh ban đầu.
Bài toán này là NP, không có thuật toán tối ưu với độ phức tạp đa thức. Tên gọi phổ biến của bài này là Traveling Salesman Problem (TSP).
Khi gặp bài NP, ta chỉ có thể tìm cách đưa ra một kết quả càng tối ưu càng tốt. Một số phương pháp thường dùng là tham lam hoặc local search - sẽ được nói trong bài viết này.
Bạn có thể nộp thử bài này ở VNOJ.
¶ Tham Lam
Một thuật toán rất hồn nhiên nhất là, xuất phát từ điểm thứ 1, tại mỗi bước, ta sẽ di chuyển đến điểm gần nó nhất (mà chưa được di chuyển đến trước đó). Lặp lại N lần, ta thu được một chu trình.
Cài đặt 1 số phần chính:
struct Point {
double x, y;
Point(double x = 0, double y = 0) : x(x), y(y) {}
Point operator - (Point a) { return Point(x-a.x, y-a.y); }
double len() { return sqrt(x*x + y*y); }
} a[MAXN];
bool used[MAXN]; // Đánh dấu điểm đã được đi qua.
int id[MAXN]; // Lưu chỉ số của các điểm trong kết quả tìm được.
void solve() {
memset(used, false, sizeof used);
used[1] = true;
id[1] = 1;
for(int i = 2; i <= n; ++i) {
double bestDist = 1e6;
int save = -1;
for(int j = 1; j <= n; ++j) {
double curDist = (a[current.id[i-1]] - a[j]).len();
if (!used[j] && curDist < bestDist) {
bestDist = curDist;
save = j;
}
}
id[i] = save;
used[save] = true;
}
}
Dưới đây là kết quả khi mình chạy với một bộ test được sinh random gồm 50 đỉnh:
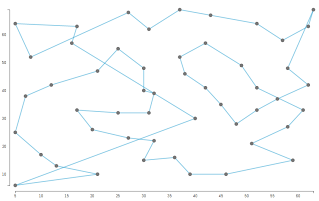
Khi quan sát kết quả của thuật toán trên, dễ thấy có rất nhiều cặp cạnh cắt nhau. Khi tồn tại 2 cạnh AB và CD cắt nhau, ta có thể đảo nó thành AC và BD hoặc AD và BC, và giữ nguyên phần còn lại của chu trình. Như vậy ta có thể thu được một kết quả tốt hơn. Nhận xét này đưa ta đến với ý tưởng thứ 2:
¶ Local Search
Xét một chu trình ban đầu bất kỳ. Xét tất cả cặp cạnh, với mỗi cặp cạnh u, v, ta có chu trình 1 --> u-1 --> u --> v-1 --> v --> 1, ta thử đổi nó thành 1 --> u-1 --> v-1 --> u --> v --> 1. Nếu việc đổi này cho ta một chu trình có trọng số nhỏ hơn, ta giữ lại chu trình mới này.
Cài đặt:
void optimize() {
while (true) {
bool stop = true;
for(int u = 2; u <= n; ++u) {
for(int v = n-1; v > u; --v) {
// t1 = (cạnh (u-1) --> u) + (cạnh (v --> (v+1))
double t1 = (a[id[u-1]] - a[id[u]]).len()
+ (a[id[v]] - a[id[v+1]]).len();
// t2 = (cạnh (u-1) --> v) + (cạnh (u --> (v+1))
double t2 = (a[id[u-1]] - a[id[v]]).len()
+ (a[id[u]] - a[id[v+1]]).len();
if (t1 > t2) { // Nếu đổi chu trình cho kết quả tốt hơn
for(int i = u, j = v; i <= j; ++i, --j) {
swap(id[i], id[j]);
}
stop = false;
}
}
}
if (stop) break;
}
}
Minh họa cho test trên (chú ý rằng mình cài đặt sai và không xét cạnh nối từ đỉnh cuối đến đỉnh 1, nên còn một cặp cạnh cắt nhau _):
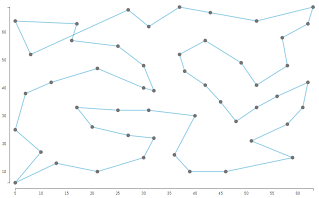
Ý tưởng này chính là nền tảng của Local Search: Xuất phát từ một cấu hình kết quả, ta tìm cách thay đổi một phần của cấu hình để đạt được một cấu hình tốt hơn. Thông thường, cài đặt local search gồm 3 bước chính:
- Khởi tạo một cấu hình kết quả bất kỳ
- Gọi C là cấu hình hiện tại. Ta xét các cấu hình "kề" với C, chọn ra cấu hình tốt nhất. Cập nhật cấu hình này cho C.
- Lặp lại đến khi ta không thể cập nhật được C.
Trong các bước trên có đề cập đến khái niệm "kề" của 2 cấu hình. Khái niệm này chỉ đơn giản là tập những cấu hình mà ta xét đến khi đang ở một cấu hình nhất định. Chẳng hạn trong bài toán mở đầu, với mỗi đường đi, các cấu hình kề nó là các đường đi nhận được khi đổi một cặp cạnh.
¶ Local Search dưới cách hiểu của đại số
Xét một bài toán tìm giá trị lớn nhất của một hàm 2 chiều J(theta0, theta1).
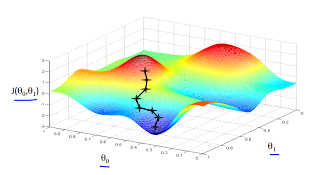
Hình vẽ trên mô tả cách làm của local search: Xuất phát từ điểm xanh đậm, ta xét các điểm ở gần nó, tìm điểm mà J lớn nhất, rồi di chuyển đến điểm đó.
¶ Bài tập áp dụng:
- ACM ICPC National Vietnam 2017 - Bài E
- Đây là một bài tập điển hình về áp dụng Local Search trong lập trình thi đấu (Competitive programming). Các bạn nên làm thử bài này trước khi làm những bài khác.
- Lời giải chi tiết
- SPOJ - PANEL
- IPSC 2013 - Invisible cats
- https://www.facebook.com/note.php?note_id=10150106829298920