¶ Thuật toán KMP
Người viết: Trịnh Quang Anh - University of Melbourne
Review bởi:
- Cao Thanh Hậu - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Lê Minh Hoàng - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Hoàng Xuân Nhật - Đại học Khoa học Tự nhiên - ĐHQG-HCM
Bài viết được dịch từ đây và đã được chỉnh sửa bổ sung thêm một số phần.
Kiến thức cần biết: Xử lý xâu cơ bản. Bạn đọc có thể xem lại các thuật ngữ và bài tập về xâu tại đây.
¶ Giới thiệu
Một trong những bài toán kinh điển nhất về xử lý xâu là bài toán so khớp chuỗi: Cho xâu độ dài và xâu độ dài , đếm số lần xuất hiện trong . Chẳng hạn, nếu và , thì xuất hiện lần tại ở các vị trí , , của . Mục tiêu của chúng ta là tìm một thuật toán tối ưu hơn để giải quyết bài toán này, thay vì duyệt từng vị trí để kiểm tra trong .
Knuth-Morris-Pratt (KMP) là một thuật toán có độ phức tạp để giải quyết bài toán so khớp chuỗi. Ý tưởng của KMP là mở rộng một hậu tố kết thúc tại sang hậu tố kết thúc tại mà vẫn đảm bảo khớp với tiền tố tương ứng, từ đó cải thiện độ phức tạp nhờ loại bỏ được thao tác so sánh xâu tốn kém. Các phần tiếp theo sẽ nói rõ các bước để đạt được điều này. Nhưng trước tiên, ta sẽ làm quen với khái niệm hàm tiền tố, một hàm giúp chúng ta phân tích kỹ hơn về các cấu trúc "tự khớp" trong xâu , và là cốt lõi của thuật toán KMP.
¶ Định nghĩa
Lưu ý: Xuyên suốt bài viết này các vị trí trong mỗi xâu sẽ được đếm từ 0.
Tiền tố chuẩn. Cho một xâu . Một tiền tố của được gọi là một tiền tố chuẩn nếu nó không là cả xâu .
Hàm tiền tố. Cho một xâu có độ dài . Hàm tiền tố của được định nghĩa là một mảng có độ dài , trong đó là độ dài của tiền tố chuẩn dài nhất của xâu con mà cũng là hậu tố của xâu con này. Từ định nghĩa này ta có .
Biểu diễn toán học của hàm tiền tố:
Ví dụ, hàm tiền tố của xâu "" là và hàm tiền tố của xâu "" là .
Tính nhanh hàm tiền tố là hết sức quan trọng vì nó là một bước thiết yếu trong thuật toán KMP. Ở phần sau, bài viết giới thiệu một thuật toán "ngây thơ" để tính hàm tiền tố với độ phức tạp . Từ đó, ta sẽ dùng các nhận xét để tối ưu thuật toán thành độ phức tạp .
¶ Thuật toán ngây thơ
Từ biểu diễn toán học của hàm tiền tố, ta có thể xây dựng một thuật vét cạn như sau: Với mỗi từ đến , duyệt qua mọi để kiểm tra điều kiện , khi đó là giá trị lớn nhất của có điều kiện được thỏa mãn.
vector<int> prefix_function(string s) {
int n = (int)s.length();
vector<int> pi(n, 0);
for (int i = 0; i < n; i++)
for (int k = 0; k <= i; k++)
if (s.substr(0, k) == s.substr(i - k + 1, k))
pi[i] = k;
return pi;
}
Do có cặp và so sánh hai xâu bằng s.substr() mất , độ phức tạp của thuật toán này là .
¶ Thuật toán tối ưu để tìm hàm tiền tố
Một chút bối cảnh lịch sử: Thuật toán này được tìm ra bởi Morris, chỉ vài tuần trước khi được Knuth tìm ra một cách độc lập. Morris & Pratt đăng báo cáo vào năm 1970, rồi cả ba đồng xuất bản thuật toán này vào năm 1977 (Nguồn: Wikipedia)
¶ Phép tối ưu đầu tiên
Nhận xét quan trọng đầu tiên là giá trị của hàm tiền tố chỉ có thể tăng thêm tối đa đơn vị khi duyệt từ lên .
Thật vậy, giả sử , ta lấy hậu tố kết thúc ở có độ dài và bỏ chữ cái cuối của nó đi. Xâu thu được là một hậu tố kết thúc ở khớp với tiền tố có cùng độ dài là , lớn hơn , mâu thuẫn với việc là hậu tố dài nhất thỏa mãn của .
Để hình dung sự mâu thuẫn này, ta xét ví dụ dưới đây. Ở vị trí , hậu tố dài nhất mà cũng là tiền tố có độ dài (), và ở vị trí thì ta có . Khi đó, xâu bằng xâu , dẫn tới hai xâu và bằng nhau. Do đó, phải bằng chứ không phải .
Do đó, khi duyệt sang vị trí tiếp theo, giá trị của hàm tiền tố chỉ có thể tăng thêm , giữ nguyên, hoặc giảm đi.
Chỉ riêng nhận xét này là đủ để chúng ta giảm độ phức tạp xuống còn : Thay vì mỗi lần duyệt xét mọi giá trị có thể của , thuật toán bắt đầu với (hàm tiền tố tăng tối đa nên đây là giá trị lớn nhất có thể của ) và giảm dần đến khi so khớp thành công. Vì hàm tiền tố suốt cả quá trình duyệt chỉ có thể tăng tối đa bước, dẫn tới chỉ có tối đa bước giảm , nên số bước thực hiện so sánh hai xâu chỉ còn là . Vì vậy, độ phức tạp tổng của thuật chỉ còn là (so sánh xâu vẫn là ).
vector<int> prefix_function(string s) {
int n = (int)s.length();
vector<int> pi(n, 0);
for (int i = 1; i < n; i++)
int k = pi[i - 1] + 1;
while (k && s.substr(0, k) != s.substr(i - k + 1, k))
k--;
pi[i] = k;
return pi;
}
Tuy nhiên, chúng ta có thể làm tốt hơn.
¶ Phép tối ưu thứ hai
Trước tiên, ta nhận thấy nhược điểm làm cho thuật toán có độ phức tạp là thao tác so sánh xâu mất .
Như đã đề cập từ đầu bài viết, ý tưởng chính để triệt tiêu thao tác này là mở rộng một hậu tố kết thúc ở đã khớp tiền tố để có được một hậu tố kết thúc ở cũng khớp với tiền tố.
Cụ thể, nếu ta có một hậu tố kết thúc tại khớp với tiền tố cùng độ dài , và ta có , thì hậu tố kết thúc tại có độ dài khớp với tiền tố có độ dài .
Vậy nếu ta nhanh chóng duyệt qua được các giá trị là độ dài cho cặp tiền tố - hậu tố ứng với đã khớp sẵn, theo thứ tự giảm dần, thì giá trị đầu tiên (và lớn nhất) cũng thỏa mãn cho ta biết . Nói cách khác, nhờ có cặp xâu khớp sẵn mà ta chỉ cần so sánh một cặp ký tự (thao tác có thể thực hiện trong ), và từ đó loại bỏ được thao tác so sánh xâu.
Ta bắt đầu duyệt bằng cách xét hậu tố kết thúc tại có độ dài . Từ định nghĩa hàm tiền tố, hậu tố này khớp với tiền tố có độ dài . Nếu , ta có thể khẳng định được rằng vì chỉ tăng tối đa khi từ sang .
Nếu , ta duyệt đến hậu tố kết thúc tại có độ dài lớn nhì, và khớp với tiền tố cùng độ dài.
Nếu đặt độ dài này là thì ta có (từ định nghĩa) và :
Tuy nhiên, do hậu tố kết thúc ở độ dài cũng khớp với tiền tố độ dài là , hậu tố độ dài kết thúc ở khớp với tiền tố độ dài .
Do lớn nhất, ta phải có . Nói cách khác, độ dài hậu tố lớn thứ nhì kết thúc ở mà khớp với tiền tố tương ứng là . So sánh và , nếu chúng bằng nhau thì ta có .
Minh họa cho hai trường hợp trên:
Nếu , lập luận tương tự, độ dài lớn thứ ba cho hậu tố kết thúc tại khớp với tiền tố là , độ dài lớn thứ tư là ,...
Từ đó, ta có thể duyệt qua mọi hậu tố kết thúc tại khớp với tiền tố độ dài như sau: Ban đầu đặt , để đến độ dài tiếp theo thỏa mãn, ta gán . Tương tự lập luận ở phần phép tối ưu đầu tiên, khi chuyển từ sang ta gán nên tăng tối đa , và khi cập nhật thì giảm ít nhất . Do đó, ta chỉ duyệt qua giá trị của và mỗi lần thao tác so sánh hai ký tự mất , đẫn đến độ phức tạp tổng là .
¶ Thuật toán cuối cùng
Tổng kết lại, thuật toán của chúng ta hoạt động như sau:
- Tính hàm tiền tố bằng cách duyệt từ đến (gán mặc định ).
- Giả sử đã tính xong . Để tính , ta khởi tạo biến mang ý nghĩa là độ dài của hậu tố dài nhất của mà chưa được kiểm tra.
- Kiểm tra liệu hậu tố của có độ dài cũng khớp với tiền tố tương ứng hay không bằng cách so sánh hai chữ cái cuối ( và ).
- Nếu chúng bằng nhau, ta tìm được . Nếu không, gán rồi lặp lại bước 3.
- Nếu mà vẫn chưa ghép cặp được với , ta đặt rồi tiếp tục tính .
¶ Cài đặt
Cài đặt các bước trên rất ngắn và trực quan:
vector<int> prefix_function(string s) {
int n = (int)s.length();
vector<int> pi(n);
for (int i = 1; i < n; i++) {
int j = pi[i - 1];
while (j > 0 && s[i] != s[j])
j = pi[j - 1];
if (s[i] == s[j])
j++;
pi[i] = j;
}
return pi;
}
Code có độ phức tạp và sử dụng bộ nhớ.
Một điểm đáng lưu ý nữa là đây là một thuật toán online: Ta có thể đọc lần lượt từng chữ cái của xâu , mỗi chữ cái mới vào có thể được xử lý ngay lập tức để tính được . Nói cách khác, nếu đề bài yêu cầu tính hàm tiền tố nhưng có thêm truy vấn "thêm một chữ cái vào cuối xâu" thì ta vẫn có thể làm như bình thường.
Về mặt bộ nhớ, ta vẫn cần phải lưu lại xâu và giá trị các hàm tiền tố trước đó nên vẫn cần đến bộ nhớ. Trường hợp đặc biệt là khi hàm tiền tố luôn nhỏ hơn một hằng số nào đó, khi đó ta chỉ cần lưu chữ cái đầu và hàm tiền tố tương ứng của xâu. Nhận xét này sẽ tỏ ra rất hữu ích ở các phần sau.
¶ Ứng dụng
¶ Thuật toán Knuth-Morris-Pratt (KMP)
Quay trở lại với bài toán ban đầu: Đếm số lần xâu độ dài xuất hiện trong xâu độ dài . Lời giải cho bài toán này - thuật toán KMP - là một áp dụng kinh điển của hàm tiền tố. Vậy làm thế nào để dùng hàm tiền tố khi có hai xâu cần khớp chứ không phải trong một xâu? Bằng cách gộp chúng vào nhau.
Nhận xét rằng nếu ta nối xâu vào sau xâu và hai xâu được ngăn cách bởi một ký tự không nằm trong cả 2 xâu (ví dụ nếu , gồm toàn chữ cái thì có thể lấy là , xâu mới là ), thì mỗi một lần xuất hiện trong tương đương với một vị trí ở xâu mới có hàm tiền tố = .
Thuật toán KMP đảm bảo tính đúng đắn, vì nếu thỏa mãn thì phải có (nghĩa là các giá trị thỏa mãn phải nằm ở nửa sau tạo bởi ) và hậu tố của có độ dài không thể "tràn" sang phần của .
Ta có thể cài đặt KMP bằng cách sử dụng code trên: prefix_function(s + # + t) trả về hàm tiền tố cho và ta chỉ cần đếm xem có bao nhiêu phần tử trong đó có giá trị là . Cách cài đặt này tốn bộ nhớ.
Tuy nhiên, việc chọn ký tự ngăn cách là một chữ cái không nằm trong cả hai xâu còn dẫn đến . Như đã nói ở trên, chặn trên này cho phép ta chỉ lưu xâu và hàm tiền tố của xâu này. Với các vị trí thuộc xâu thì ta có thể tính lần lượt (bằng cách lưu một biến chứa giá trị ở vị trí hiện tại) và thêm vào đáp án nếu tại vị trí đang xét là :
vector<int> pi = prefix_function(s);
int ans = 0; // Số lần s xuất hiện trong t
int j = 0; // Hàm tiền tố ở vị trí đang xét của xâu t
for (int i = 0; i < m; i++) {
while (j > 0 && t[i] != s[j])
j = pi[j - 1];
if (t[i] == s[j])
j++;
if (j == n)
ans++;
}
Code trên lưu cả hai xâu , nên vẫn dùng bộ nhớ, nhưng có thể giảm xuống còn bộ nhớ nếu ta đọc lần lượt từng ký tự của rồi tính luôn thay vì lưu cả xâu rồi mới tính.
Tổng kết lại, thuật toán KMP giải quyết được bài toán so khớp chuỗi trong thời gian và sử dụng bộ nhớ.
¶ Đếm số lần xuất hiện của từng tiền tố
Bài toán
Ở đây ta xét hai bài toán tương đối giống nhau:
Cho một xâu độ dài .
- Với mỗi , đếm số lần tiền tố xuất hiện trong xâu .
- Thay vì đếm trong xâu , đếm số lần xuất hiện trong một xâu khác có độ dài .
Lời giải
Trước tiên, ta giải phiên bản 1.
Xét giá trị của tại vị trí . Dựa vào định nghĩa của , một trong các hậu tố của là tiền tố . lớn nhất nên không thể có tiền tố nào dài hơn mà cũng khớp với một hậu tố của , nhưng có thể có một số tiền tố ngắn hơn thỏa mãn.
Ý tưởng là duyệt qua mỗi và kiểm soát xem số lần các tiền tố xuất hiện thay đổi như thế nào. Xét các hậu tố kết thúc ở mà khớp với tiền tố có cùng độ dài, khi đó ta đơn giản cộng một vào số lần xuất hiện của các tiền tố này.
Như đã đề cập ở phần thuật toán cuối cùng, độ dài các tiền tố mà cũng là hậu tố kết thúc ở từ lớn đến bé là , , Ta duyệt qua lần lượt từng tiền tố này rồi cộng vào đáp án cho tiền tố đó (đáp án cho tiền tố độ dài là ), thì độ phức tạp sẽ là :
vector<int> ans(n, 0);
for (int i = 0; i < n; i++) {
for (int j = i; pi[j]; j = pi[j] - 1) {
ans[j]++;
if (!pi[j]) {
break;
}
}
}
Thuật toán trên có độ phức tạp lớn do mỗi tiền tố ta phải duyệt qua nhiều lần. Để khắc phục điều này, ta sẽ dùng ý tưởng tương tự như mảng cộng dồn.
Để ý rằng nếu ta xét đồ thị cho đỉnh , trong đó đỉnh ứng với tiền tố thứ , và có các cạnh nối từ đến với mọi từ đến , thì đồ thị này là một cây có hướng.
Ví dụ: với xâu "", ta có hàm tiền tố , tương ứng với các cạnh của cây:
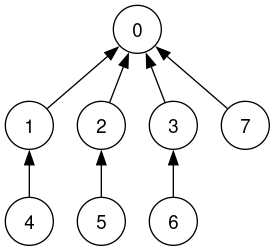
Ý tưởng này phần nào giúp chúng ta dễ hình dung hơn cách giải: việc tính đưa về bài toán cập nhật truy vấn cộng vào các nút trên đường đi từ một nút đến gốc và tìm giá trị tại tất cả các nút sau mọi truy vấn - một bài toán có cách giải dùng mảng cộng dồn.
Giả sử cần cộng vào các giá trị , ,... Thay vì duyệt qua từng giá trị một ta chỉ gán . Sau đó, duyệt giảm dần từ về , khi duyệt đến thì cộng vào khi duyệt đến thì cộng vào , khi duyệt đến thì cộng vào ,... Đến khi duyệt xong thì giá trị của , ,... đều là đã được cộng thêm 1.
Do ta duyệt qua mỗi phần tử đúng một lần và độ phức tạp tính hàm tiền tố là , tổng độ phức tạp thuật chỉ còn là .
vector<int> ans(n, 1);
for (int i = n - 1; i > 0; i--)
if (pi[i])
ans[pi[i] - 1] += ans[i];
Để giải quyết phiên bản thứ 2, ta chỉ cần áp dụng kỹ thuật được sử dụng ở thuật toán KMP: nối hai xâu để tạo xâu mới và xây dựng hàm tiền tố cho xâu này. Sau đó, tìm tương tự như phiên bản 1, đáp án là của các vị trí thuộc về xâu ().
¶ Đếm số xâu con phân biệt trong một xâu
Bài toán
Cho một xâu có độ dài . Đếm số xâu con phân biệt của .
Lời giải
Hướng làm của chúng ta là bắt đầu với xâu rỗng, rồi mở rộng xâu bằng cách thêm lần lượt vào cuối xâu, đồng thời cập nhật số xâu con phân biệt hiện tại. Sau khi đã thêm đủ ký tự , ta sẽ có được số xâu con phân biệt của xâu ban đầu.
Mỗi lần thêm ký tự ta sẽ có thêm xâu mới là , nhưng ta chỉ được thêm vào đáp án các xâu không nằm trong xâu trước khi thêm (hay nói cách khác là không nằm trong ). Làm thế nào để đếm nhanh số xâu không lặp này? Một lần nữa ta sử dụng hàm tiền tố.
Gọi xâu có được sau khi thêm vào cuối là . Nhận xét là nếu ta đảo ngược xâu thì số xâu bị lặp chính là số tiền tố của khớp với một xâu con nào đó của . Nếu ta tính hàm tiền tố trên xâu bị đảo ngược, thì số xâu bị lặp này chính là giá trị lớn nhất của vì:
- khớp với một xâu trong không phải chính nó (theo định nghĩa hàm tiền tố) nên nó bị lặp, dẫn các xâu cũng bị lặp.
- Các xâu có độ dài lớn hơn chắc chắn không lặp vì nếu có thì sẽ không phải giá trị lớn nhất của .
Vậy số xâu mới bị lặp với một xâu con có trước là , dẫn đến số xâu cần thêm vào đáp án là (Do có xâu mới). Tính với mỗi hết nên tổng độ phức tạp thuật toán là .
Ngoài ra, thay vì mỗi bước cập nhật kết quả sau khi thêm một chữ cái vào cuối xâu hiện tại, ta cũng có thể thêm một chữ vào đầu xâu hiện tại, hoặc bắt đầu với xâu hoàn chỉnh và mỗi bước bỏ đi chữ cái đầu (hoặc cuối). Độ phức tạp cũng chưa phải là độ phức tạp tốt nhất - ta có thể đếm số xâu con của một xâu trong hoặc nhờ mảng hậu tố (Suffix Array).
¶ Nén xâu
Bài toán
Cho một xâu độ dài . Tìm xâu có độ dài nhỏ nhất sao cho có thể tạo được xâu bằng cách lặp lại xâu hữu hạn lần.
Lời giải
Trước tiên, nhận xét là chúng ta chỉ cần tìm độ dài của , vì khi đó đáp án của bài toán sẽ là tiền tố của có độ dài này.
Giả sử ta cố định độ dài của là (chỉ xét là ước của ) thì khi đó bài toán đưa về kiểm tra có được thỏa mãn hay không.
Nếu ta dùng thẳng điều kiện ), với mỗi giá trị của kiểm tra sẽ cần duyệt qua cặp xâu liền kề, mỗi cặp kiểm tra xem chúng bằng nhau không mất độ phức tạp , nên độ phức tạp để kiểm tra khi cố định là . chỉ có thể nhận giá trị khác nhau do là ước của , dẫn tới tổng độ phức tạp là . Độ phức tạp này là đủ tốt để AC với , nhưng ta có thể dùng hàm tiền tố để làm tốt hơn.
Chìa khóa ở đây là thay đổi cách viết thành:
Rồi gộp các xâu ở các vế trái thành một, gộp các xâu ở các vế phải thành một, ta thu được:
Hay nói cách khác, phải thỏa mãn tiền tố độ dài khớp với hậu tố có cùng độ dài của xâu. Kiểm tra điều kiện rút gọn này là đủ vì từ nó ta có thể suy ngược lại ra điều kiện . Áp dụng hàm tiền tố: Các tiền tố mà cũng là hậu tố kết thúc tại có độ dài , duyệt qua từng độ dài này và dừng lại khi có một độ dài thỏa mãn chia hết cho , khi đó đáp án sẽ là . Nếu không có độ dài nào thỏa mãn, đáp án khi đó là . Độ phức tạp của thuật chỉ là .
Thậm chí ta chỉ cần kiểm tra cho tiền tố độ dài là đủ: nếu là ước của thì đó chính là đáp án, nếu không thì đáp án là . Chứng minh:
- Nếu chia hết cho , do là tiền tố dài nhất cũng là hậu tố của xâu, là độ dài ngắn nhất thỏa mãn.
- Nếu không chia hết cho , giả sử phản chứng tồn tại sao cho nén được xâu thành tiền tố độ dài của xâu. Khi đó ta có > , dẫn đến hậu tố độ dài của xâu sẽ chứa một phần của .
Xét xâu . Do tiền tố và hậu độ dài bằng nhau, , so sánh từng cặp chữ cái tương ứng của hai xâu này, ta rút ra .
Đặt , điều kiện trên khi đó tương đương với , nghĩa là là một xâu nén của . Do , là một xâu nén của có độ dài nhỏ hơn , mâu thuẫn với cách chọn là xâu nén nhỏ nhất. Ta có điều phải chứng minh.
Ví dụ minh họa: