¶ Z-function
Người viết: Nguyễn Nhật Minh Khôi - Đại học Khoa học Tự nhiên - ĐHQG-HCM
Reviewer:
- Trần Quang Lộc - ITMO University
- Hồ Ngọc Vĩnh Phát - Đại học Khoa học Tự nhiên - ĐHQG-HCM
- Nguyễn Phú Bình - THPT chuyên Hùng Vương, Bình Dương
- Nguyễn Hoàng Vũ - THPT chuyên Phan Bội Châu, Nghệ An
Tham khảo: cp-algorithm
¶ Định nghĩa
Trong blog này, chúng ta sẽ tìm hiểu về hàm (Z-function) của một chuỗi và những ứng dụng của nó.
Cho một chuỗi độ dài , ký hiệu là , ta có hàm tương ứng là một mảng , với là độ dài tiền tố chung lớn nhất của chuỗi và .
Ở đây, ta sẽ quy ước hai điều: một là chuỗi và mảng sẽ mặc định bắt đầu từ , hai là , ta có thể hiểu quy ước này nghĩa là chuỗi con xét ở đây phải là chuỗi con nghiêm ngặt (tức không tính chính nó).
Ví dụ hàm với :
| i | S[0..n-1] | S[i..n-1] | z[i] |
|---|---|---|---|
| 0 | (quy ước) | ||
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 |
¶ Thuật toán ngây thơ
Thuật toán ngây thơ rất đơn giản, với mọi , ta sẽ tìm bằng cách vét cạn, bắt đầu với và tăng lên cho đến khi gặp kí tự đầu tiên không trùng và lưu ý phải hợp lệ (bé hơn hoặc bằng vị trí cuối chuỗi ). Thuật toán được trình bày như sau:
vector<int> z_function(string s) {
int n = s.length();
vector<int> z(n);
for (int i = 1; i < n; ++i)
while (i + z[i] < n && s[z[i]] == s[i + z[i]])
++z[i];
return z;
}
Độ phức tạp của thuật toán này là , trong phần sau ta sẽ tối ưu thuật toán này về độ phức tạp .
¶ Thuật toán tối ưu
Để tối ưu thuật toán, ta có một nhận xét: nếu ta đã tính được (ở đây chỉ xét ), ta có thông tin rằng đoạn khớp với đoạn . Tận dụng thông tin này, ta có thể rút ngắn quá trình tính các ở sau (). Để ngắn gọn, tạm thời đặt . Cụ thể có hai trường hợp:
- : vì đoạn giống với đoạn , do đó ta không cần duyệt lại đoạn mà chỉ cần lấy lại đã tính trước đó, tuy nhiên có thể lớn hơn , tức vượt biên đã duyệt, do đó ta chỉ lấy khởi tạo của là:
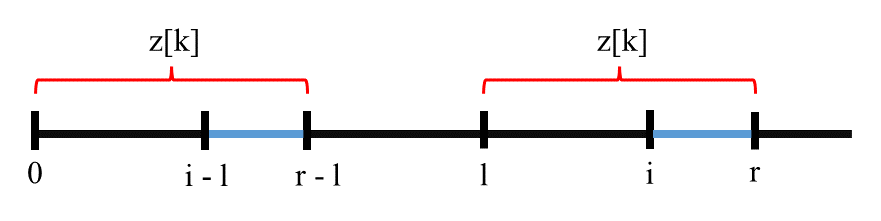
- : khi đó nằm ngoài vùng ta đã kiểm tra, khi đó ta không thể tận dụng gì nên chỉ khởi tạo và làm theo thuật toán ngây thơ.
Từ nhận xét này, ta thấy rằng nếu càng lớn, tức nào càng lớn thì ta càng có cơ hội khởi tạo được lớn hơn (tức ít phải xét lại hơn). Do đó trong quá trình tính ta sẽ duy trì hai biến và với ý nghĩa đoạn là đoạn thoả và là lớn nhất. khi đó, mỗi lần xét một mới ta sẽ khởi tạo như đã đề cập ở trên. Sau khi tính xong , ta sẽ cập nhật lại và với đoạn mới tính. Từ đó ta có thuật toán cải tiến như sau:
vector<int> z_function(string s) {
int n = s.length();
vector<int> z(n);
for (int i = 1, l = 0, r = 0; i < n; ++i) {
// khoi tao z[i] theo thuat toan toi uu
if (i <= r)
z[i] = min(r - i + 1, z[i - l]);
// tinh z[i]
while (i + z[i] < n && s[z[i]] == s[i + z[i]])
++z[i];
// cap nhat doan [l,r]
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
return z;
}
Lưu ý rằng ở đây ta khởi tạo để đảm bảo đây là một đoạn không chứa bất kỳ nào.
Để chứng minh thuật toán tối ưu ta sẽ xem xét số phép tính trong vòng lặp while. Dễ thấy rằng, mỗi vị trí sẽ chỉ có hai trường hợp sau:
- : khi này nếu thì vòng lặp while sẽ chỉ lặp một lần, sẽ được giữ nguyên. Ngược lại, nếu thì sau khi chạy, do nên chắc chắn , khi đó ta sẽ tăng lên thành .
- : ta có hai trường hợp nhỏ nữa:
- : do ta đã kiểm soát được nên rõ ràng sẽ không thể tăng lên nữa, do đó vòng lặp while sẽ dừng sau lần kiểm tra điều kiện đầu tiên, sẽ được giữ nguyên.
- : khi đó, do ta chưa biết phía sau đoạn có khớp tiếp không, nên có thể vòng while sẽ phải chạy thêm nữa. Tuy nhiên, khi chạy xong, chắc chắn chỉ có thể giữ nguyên (không có thêm ký tự khớp nên ) hoặc tăng lên (có thêm ký tự khớp nên ).
Từ hai nhận xét này, ta thấy một điều quan trọng, đó là phép toán ++z[i] luôn làm tăng . Mà chỉ có thể tăng chứ không giảm, hơn nữa giá trị tối đa chỉ có thể là nên số lần tăng của chỉ có thể là . Từ hai điều này, ta kết luận rằng vòng lặp while chỉ lặp không quá lần phép ++z[i] trong suốt quá trình tính . Do đó, độ phức tạp của thuật toán đã cho là .
Kĩ thuật hai con trỏ cũng là một cách giải thích khác cho thuật toán này. Ta có thể tưởng tượng và là hai con trỏ luôn tăng, việc thực hiện phép ++z[i] trong vòng lặp while cũng tương đương với việc tăng lên một đơn vị ( lúc này sẽ được gán lại bằng hiện tại). Khi đó, vì không bao giờ tăng quá lần nên phép ++z[i] cũng không bao giờ thực hiện quá lần, ta kết luận thuật toán có độ phức tạp .
¶ Một số ứng dụng
¶ So khớp chuỗi
Cho chuỗi độ dài và độ dài , ta cần tìm chuỗi con liên tục trong sao cho chuỗi con đó bằng với chuỗi . Bạn đọc có thể nộp bài ở VNOJ.
Thuật toán trong trường hợp này rất đơn giản, ta chỉ cần tạo chuỗi mới , khi đó ta chỉ cần tính của chuỗi mới này và chọn ra các có . Ở đây, là một ký tự đặc biệt dùng để phân tách và trong chuỗi , đảm bảo không vượt quá độ dài của , ký tự này phải thoả điều kiện là không nằm trong cả chuỗi và chuỗi .
Giả sử \diamond = \texttt{#} , thuật toán có thể cài đặt bằng ngôn ngữ C++ như sau:
vector<int> string_matching(string s, string t) {
string p = t + '#' + s;
int m = t.length();
int n = s.length();
vector<int> z = z_function(p);
vector<int> res;
for (int i = m + 1; i <= m + n; ++i) {
// tim duoc dap an va them vao vector res
if (z[i] == m)
res.push_back(i - m - 1);
}
return res;
}
¶ Số lượng chuỗi con phân biệt trong một chuỗi
Cho chuỗi có độ dài , ta cần tìm số lượng chuỗi con phân biệt của .
Chúng ta sẽ giải quyết bài này một cách tuần tự như sau: biết được số lượng chuỗi con phân biệt của chuỗi hiện tại là , ta thêm một ký tự vào, đếm xem có bao nhiêu chuỗi con phân biệt mới của và cập nhật lại .
Gọi là chuỗi thu được bằng cách viết ngược từ ký tự cuối tới ký tự đầu của , ta nhận xét rằng các chuỗi con phân biệt mới sẽ luôn kết thúc tại . Khi đó nhiệm vụ của chúng ta tương ứng với việc đếm xem có bao nhiêu tiền tố của không xuất hiện ở bất cứ đâu trong . Ta sẽ làm điều đó bằng cách tính hàm của và tìm giá trị lớn nhất . Rõ ràng là các chuỗi con có độ dài và nhỏ hơn đều xuất hiện lần thứ hai đâu đó trong , còn các chuỗi con có độ dài lớn hơn sẽ chưa xuất hiện. Do đó, số lượng chuỗi con mới xuất hiện là .
Vậy, thuật toán của chúng ta sẽ có vòng lặp tăng từ đến , tại mỗi , biết được số lượng chuỗi phân biệt hiện tại là , ta sẽ tính xem số lượng chuỗi con mới xuất hiện khi thêm vào chuỗi đã xét và cập nhật lại số lượng chuỗi phân biệt. Độ phức tạp của thuật toán này là .
int num_substr(string s) {
vector<int> z = z_function(s);
string tmp;
int k = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
tmp = s[i] + tmp;
vector<int> z = z_function(tmp);
int zmax = *max_element(z.begin(), z.end());
k += (i + 1) - zmax;
}
return k;
}
Chú ý rằng thay vì thêm dần dần ký tự vào cuối chuỗi , ta có thể làm điều ngược lại là bỏ dần các ký tự ở đầu chuỗi , độ phức tạp của hai cách làm này là tương đương nhau.
¶ Period finding
Cho chuỗi độ dài , ta cần tìm chuỗi ngắn nhất sao cho ta có thể tạo ra bằng cách ghép một hoặc nhiều bản sao của chuỗi lại.
Cách giải bài này là tính hàm cho , sau đó xét các mà chia hết cho và dừng lại ở đầu tiên thoả . Khi đó kết quả của chúng ta là .
int length_compress(string s) {
vector<int> z = z_function(s);
int n = s.length();
for (int i = 1; i < n; ++i) {
if (n % i == 0 && i + z[i] == n)
return i;
}
return n;
}
Tính đúng đắn của thuật toán đã được chứng minh ở phần Compressing a string trong link này.