¶ Tổng Minkowski của các bao lồi
Người viết:
- Đặng Đoàn Đức Trung - UT Austin
Reviewer:
- Nguyễn Hoàng Vũ - Trường Đại học Công nghệ - ĐHQGHN
- Trần Xuân Bách - Đại học Chicago (Mỹ)
¶ Giới thiệu
Một số bài toán trung bình khó yêu cầu người giải phải thực hiện thao tác ghép hai bao lồi như sau: với hai bao lồi và , dựng một đa giác chỉ bao gồm các điểm với và (ở đây một điểm thuộc bao lồi nếu nó nằm trong/trên bao lồi, và việc cộng điểm được thực hiện như việc cộng véctơ). Đây chính là việc tìm tổng Minkowski của hai bao lồi và .
Ở bài viết sau, chúng ta hãy cùng xem qua cách tìm tổng Minkowski một cách hiệu quả, cũng như một số bài toán có thể được giải thông qua thuật toán này.
Bài viết này là phần 2 của chuỗi bài viết về các kĩ thuật xử lí bao lồi/hàm lồi; các bạn có thể đọc phần 1 ở đây. Một phần của bài viết được tham khảo từ cp-algorithm. Template code hình được lấy từ kactl.
¶ Định nghĩa
Để nhắc lại từ phần giới thiệu, ta định nghĩa tổng Minkowski của hai bao lồi và như sau:
- Với mọi điểm , tồn tại hai điểm và sao cho .
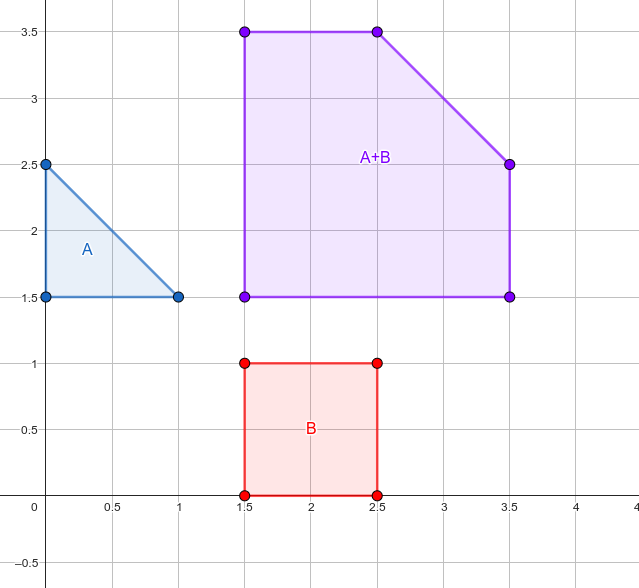 |
|---|
| Ví dụ của tổng Minkowski của hai bao lồi và |
Như ta thấy ở ví dụ trên, cũng là một bao lồi và có số lượng điểm là . Một cách tổng quát hơn, ta có thể chứng minh được là tổng cũng là đa giác lồi và có tối đa đỉnh.
¶ Thuật toán tìm tổng Minkowski của hai bao lồi
Lấy ví dụ vừa nêu trên, ta có thể nhìn dưới một góc nhìn khác như sau.
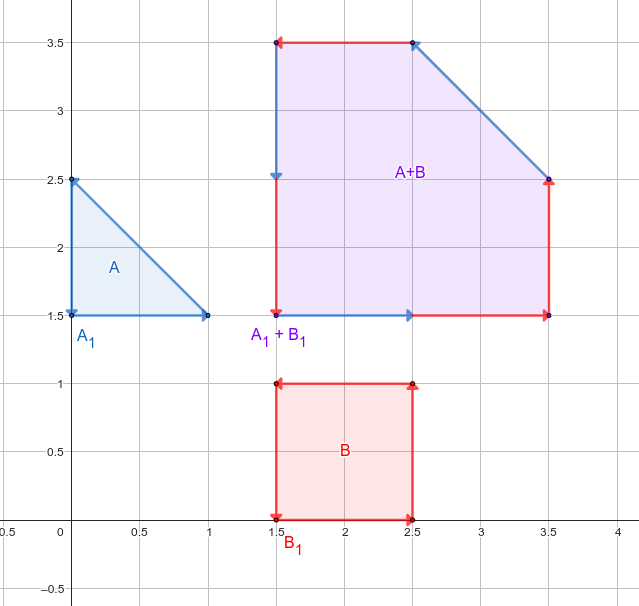
Ta có hai nhận xét sau:
- Đỉnh trái dưới của bằng đỉnh trái dưới của cộng đỉnh trái dưới của .
- Cạnh của được là hợp của các cạnh từ và các cạnh từ .
Vì thế ta có thể dựng như sau (giả sử rằng và đi ngược chiều kim đồng hồ và được xoay lại sao cho và là đỉnh trái dưới của và ):
- Xuất phát với và . Thêm đỉnh vào đáp án.
- Ở mỗi bước, so sánh góc của và . Tăng con trỏ tương ứng với cạnh có góc nhỏ hơn theo hướng ngược chiều kim đồng hồ (tăng cả hai nếu góc của hai cạnh bằng nhau) và thêm vào đáp án.
Ta có thể coi thuật toán này như việc sắp xếp cạnh của hai bao lồi và : do cạnh của và đã được sắp xếp sẵn ngược chiều kim đồng hồ, ta chỉ cần chạy thuật toán ghép hai mảng đã được sắp xếp giống như bước ghép trong merge sort.
Dưới đây là một cách cài đặt mẫu:
// rút gọn từ kactl: https://github.com/kth-competitive-programming/kactl/blob/main/content/geometry/Point.h
template<class T>
struct Point {
typedef Point P;
T x, y;
explicit Point(T x=0, T y=0) : x(x), y(y) {}
bool operator<(P p) const { return tie(x,y) < tie(p.x,p.y); }
bool operator==(P p) const { return tie(x,y)==tie(p.x,p.y); }
P operator+(P p) const { return P(x+p.x, y+p.y); }
T cross(P p) const { return x*p.y - y*p.x; }
};
template<class P>
vector<P> minkowskiSum(vector<P> a, vector<P> b) {
// xoay a và b sao cho điểm trái dưới là điểm đầu tiên
rotate(begin(a), min_element(begin(a), end(a)), end(a));
rotate(begin(b), min_element(begin(b), end(b)), end(b));
int n = a.size(), m = b.size();
vector<P> h(n + m + 1); h[0] = a[0] + b[0];
int t = 1;
// ở đây ta cho phép i đi tới n và j đi tới m để thể hiện việc đã duyệt qua hết các cạnh của A và B
for (int i = 0, j = 0; i < n || j < m; ) {
if (i == n) j++;
else if (j == m) i++;
else {
P pa = a[(i + 1) % n] - a[i], pb = b[(j + 1) % m] - b[j];
auto cr = pa.cross(pb);
if (cr >= 0) i++;
if (cr <= 0) j++;
}
h[t++] = (a[i % n] + b[j % m]);
}
return {h.begin(), h.begin() + t - (t >= 2 && h[0] == h[t - 1])};
}
Độ phức tạp của thuật toán là .
¶ Một số bài toán ví dụ
¶ CF 87E - Mogohu-Rea Idol
Link bài: CF 87E.
¶ Đề bài
Cho ba bao lồi , và và truy vấn. Với mỗi truy vấn, ta được nhận một điểm , và ta cần trả lời rằng có tồn tại ba điểm , , và sao cho điểm là trọng tâm của tam giác được tạo bởi ().
¶ Phân tích
Nhận xét rằng là trọng tâm của tam giác tạo bởi khi và chỉ khi . Nói cách khác, điểm phải thuộc tổng Minkowski . Vì thế, ta chỉ cần dựng trước , và với mỗi truy vấn ta chỉ cần kiểm tra nếu điểm thuộc bao lồi này không là được.
¶ Cài đặt
Các bạn có thể tham khảo cách cài đặt tại đây. Ở phần cài đặt này, hàm minkowskiSum nhận một tập các bao lồi (không nhất thiết chỉ là 2 bao lồi) và trả về tổng Minkowski của tập bao lồi này. Độ phức tạp là , với là số lượng điểm trong tổng Minkowski.
¶ Tìm khoảng cách giữa hai bao lồi
¶ Đề bài
Cho hai bao lồi và , tìm khoảng cách ngắn nhất giữa hai điểm bất kì thuộc hai bao lồi này. Nếu và có điểm chung thì in ra 0 ().
¶ Phân tích
Đây là một bài toán kinh điển sử dụng tổng Minkowski. Nhận xét là bài toán có thể được viết như sau (ở đây là khoảng cách của tới gốc tọa độ):
Vì thế, nếu ta gọi chứa tất cả các điểm khi thì bài toán tương đương với việc tìm . Gọi là tổng Minkowski của bao lồi và , thì bài toán trở thành: tìm điểm trong gần gốc tọa độ nhất. Bài toán này ta có thể giải một cách dễ dàng: nếu chứa gốc tọa độ thì đáp án là , ngược lại thì ta có thể lặp qua cạnh của và tìm khoảng cách ngắn nhất từ gốc tọa độ tới từng cạnh của .
¶ Cài đặt
Các bạn có thể tham khảo cách cài đặt dưới đây.
#include <bits/stdc++.h>
using namespace std;
/// KACTL
#define rep(i, a, b) for(int i = a; i < (b); ++i)
#define all(x) begin(x), end(x)
#define sz(x) (int)(x).size()
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
template <class T> int sgn(T x) { return (x > 0) - (x < 0); }
template<class T>
struct Point {
typedef Point P;
T x, y;
explicit Point(T x=0, T y=0) : x(x), y(y) {}
bool operator<(P p) const { return tie(x,y) < tie(p.x,p.y); }
bool operator==(P p) const { return tie(x,y)==tie(p.x,p.y); }
P operator+(P p) const { return P(x+p.x, y+p.y); }
P operator-(P p) const { return P(x-p.x, y-p.y); }
P operator*(T d) const { return P(x*d, y*d); }
P operator/(T d) const { return P(x/d, y/d); }
T dot(P p) const { return x*p.x + y*p.y; }
T cross(P p) const { return x*p.y - y*p.x; }
T cross(P a, P b) const { return (a-*this).cross(b-*this); }
T dist2() const { return x*x + y*y; }
double dist() const { return sqrt((double)dist2()); }
// angle to x-axis in interval [-pi, pi]
double angle() const { return atan2(y, x); }
P unit() const { return *this/dist(); } // makes dist()=1
P perp() const { return P(-y, x); } // rotates +90 degrees
P normal() const { return perp().unit(); }
// returns point rotated 'a' radians ccw around the origin
P rotate(double a) const {
return P(x*cos(a)-y*sin(a),x*sin(a)+y*cos(a)); }
friend ostream& operator<<(ostream& os, P p) {
return os << "(" << p.x << "," << p.y << ")"; }
};
template<class P> bool onSegment(P s, P e, P p) {
return p.cross(s, e) == 0 && (s - p).dot(e - p) <= 0;
}
template<class P>
int sideOf(P s, P e, P p) { return sgn(s.cross(e, p)); }
using P = Point<double>;
bool inHull(const vector<P>& l, P p, bool strict = true) {
int a = 1, b = sz(l) - 1, r = !strict;
if (sz(l) < 3) return r && onSegment(l[0], l.back(), p);
if (sideOf(l[0], l[a], l[b]) > 0) swap(a, b);
if (sideOf(l[0], l[a], p) >= r || sideOf(l[0], l[b], p)<= -r)
return false;
while (abs(a - b) > 1) {
int c = (a + b) / 2;
(sideOf(l[0], l[c], p) > 0 ? b : a) = c;
}
return sgn(l[a].cross(l[b], p)) < r;
}
double segDist(P s, P e, P p) {
if (s==e) return (p-s).dist();
auto d = (e-s).dist2(), t = min(d,max(.0,(p-s).dot(e-s)));
return ((p-s)*d-(e-s)*t).dist()/d;
}
/// END KACTL
template<class P>
vector<P> minkowskiSum(vector<P> a, vector<P> b) {
rotate(begin(a), min_element(begin(a), end(a)), end(a));
rotate(begin(b), min_element(begin(b), end(b)), end(b));
int n = a.size(), m = b.size();
vector<P> h(n + m + 1); h[0] = a[0] + b[0];
int t = 1;
for (int i = 0, j = 0; i < n || j < m; ) {
if (i == n) j++;
else if (j == m) i++;
else {
P pa = a[(i + 1) % n] - a[i], pb = b[(j + 1) % m] - b[j];
auto cr = pa.cross(pb);
if (cr >= 0) i++;
if (cr <= 0) j++;
}
h[t++] = (a[i % n] + b[j % m]);
}
return {h.begin(), h.begin() + t - (t >= 2 && h[0] == h[t - 1])};
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n, m; cin >> n >> m;
vector<P> a(n), b(m);
vector<vector<P>> poly(n, {P(0, 0)});
for (int i = 0; i < n; i++) {
cin >> a[i].x >> a[i].y;
}
for (int i = 0; i < m; i++) {
cin >> b[i].x >> b[i].y;
b[i] = P(0, 0) - b[i]; // lật B qua gốc tọa độ
}
auto sum = minkowskiSum(a, b);
if (inHull(sum, P(0, 0), false)) {
cout << "0.0\n";
} else {
double ans = numeric_limits<double>::max();
int s = sum.size();
for (int i = 0; i < s; i++) {
ans = min(ans, segDist(sum[i], sum[(i + 1) % s], P(0, 0)));
}
cout << fixed << setprecision(10) << ans << '\n';
}
}
Độ phức tạp của thuật toán là .