¶ Các kiến thức cơ bản về Tổ hợp (Combinatorics)
Nguồn: HackerEarth
Người dịch: Bùi Việt Dũng
¶ Tập hợp (Set)
¶ Tập hợp (Set) là gì?
Trong toán học, tập hợp là một nhóm các phần tử, mỗi phần tử phân biệt với nhau.
Ví dụ, 2, 4, 6 được coi là các phần tử phân biệt khi ta xét từng số một, nhưng khi chúng ta nhóm ba số ấy thì ta được một tập hợp gồm ba phần tử được kí hiệu là {2,4,6}.
Tập hợp là một trong những khái niệm cơ bản trong Toán học.
Tập hợp các hình đa giác được biểu diễn trong biểu đồ Venn.
¶ Tập con (Subset)
Nếu mọi phần tử thuộc tập cũng thuộc tập hợp , thì tập là tập con của tập , kí hiệu là .
Tương tự, ta có thể viết , đọc là là tập cha (superset) của tập .
Quan hệ cha-con giữa các tập hợp còn được gọi là quan hệ chứa nhau (containment) hay quan hệ bao hàm (inclusion).
Nếu là tập con của tập nhưng không bằng tập , thì được gọi là tập con không tầm thường (proper subset) của tập , kí hiệu là , hay (đọc là là tập cha không tầm thường (proper superset) của tập ).
Ví dụ:
-
{1,3} {1,2,3,4}
-
{1,2,3,4} {1,2,3,4}
Tập rỗng (empty set, kí hiệu ) là tập con của tất că các tập và tất cả các tập là tập con của chính nó:
-
.
-
.
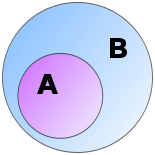
là tập con của tập .
¶ Các phép toán với tập hợp
Có nhiều phép toán có khả năng xây dựng một tập hợp mới dựa trên các tập hợp đã cho.
¶ Phép hợp (Union)
Hai tập hợp có thể được ghép vào nhau. Hợp của hai tập hợp và , kí hiệu là , là một tập hợp gồm các phần tử thuộc tập hoặc thuộc tập .
Ví dụ:
- {1,2} {1,2} = {1,2}
- {1,2} {2,3} = {1,2,3}
- {1,2,3} {3,4,5} = {1,2,3,4,5}
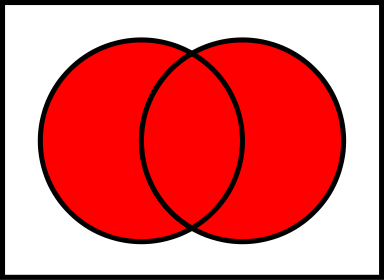
Hợp của hai tập hợp và , kí hiệu là .
Một vài tính chất cơ bản của phép hợp:
-
.
-
.
-
.
-
.
-
khi và chỉ khi .
¶ Phép giao (Intersection)
Một tập hợp mới có thể được xây dựng từ các phẩn tử mà cả hai tập đều có. Giao cuả hai tập hợp và , kí hiệu , là tập hợp các phần tử cùng thuộc tập và tập . Nếu , tập và tập là hai tập rời nhau (disjoint).
Ví dụ:
- {1,2} {1,2} = {1,2}.
- {1,2} {2,3} = {2}.
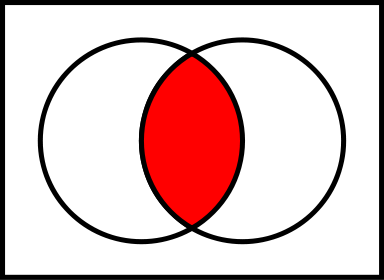
Giao của hai tập hợp và , kí hiệu là .
Một vài tính chất cơ bản của phép hợp:
-
.
-
.
-
.
-
.
-
.
-
khi và chỉ khi .
¶ Phép lấy hiệu (Relative complement)
Ta có thể thực hiên phép trừ với hai tập hợp. Hiệu của hai tập hợp và , kí hiệu là , là tập hợp bao gồm tất cả các phần tử thuộc nhưng không thuộc . Lưu ý rằng ta có thể trừ phần tử mà không thuộc tập hợp, ví dụ như bỏ phần tử 'xanh' khỏi tập hợp {1,2,3}, khi đó tập hợp {1,2,3} không bị thay đổi.
Trong một số trường hợp tập được coi là tập con của một tập lớn hơn. Trong trường hợp đó, được gọi là phần bù hoàn toàn (absolute complement) của tập , và được kí hiệu là .
Ví dụ:
-
{1,2} {1,2} = .
-
{1,2,3,4} {1,3} = {2,4}.
-
Nếu là tập hợp các số nguyên, là tập hợp các số nguyên chẵn, là tập hợp các số nguyên lẻ, khi đó .
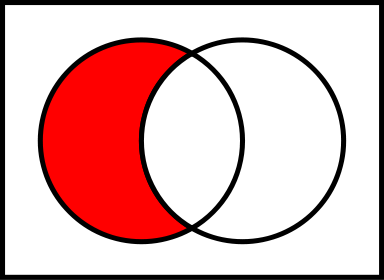
Hiệu của hai tập hợp và .
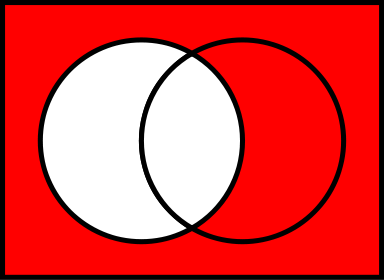
Phần bù của trong .
Một vài tính chất cơ bản của phép lấy hiệu
-
với .
-
.
-
.
-
.
-
.
-
.
-
và .
¶ Các quy tắc cơ bản
Kí hiệu là số phần tử của tập (hay còn được gọi là lực lượng của tập ).
Một vài quy tắc về tổ hợp cần nhớ:
-
Quy tắc nhân (The Rule of Product):
Giả sử có hai tập hợp và . Khi đó số cách chọn cặp gồm một phần tử thuộc tập và một phần tử thuộc tập là -
Quy tắc cộng (The Rule of Sum): Giả sử có hai tập hợp và . Khi đó số cách chọn một phần tử thuộc tập hoặc thuộc tập là nếu hai tập và rời nhau.
-
Quy tắc cộng mở rộng (sieve principle) (còn gọi là công thức bao hàm - loại trừ (Inclusion-Exclusion Formula)): .
Trong trường hợp tổng quát, ta có:
Lí do ta phải cộng trừ giao của một số tập hợp vì nếu ta không làm như vậy, ta có thể đếm nhiều lần các phần tử xuất hiện tại nhiều tập hợp khác nhau.
Các quy tắc trên cũng đúng khi ta có ba hay nhiều tập hợp.
¶ Các kiến thức cơ bản về Chỉnh hợp và Hoán vị (Permutation)
¶ Chỉnh hợp không lặp (Permutation of Distinct Objects)
Cho tập hợp gồm phần tử. Mỗi bộ gồm () phần tử được sắp thứ tự của tập hợp được gọi là một chỉnh hợp chập của phần tử thuộc .
Ví dụ: Trong trận chung kết bóng đá phải phân định thắng thua bằng đá luân lưu 11 mét. Huấn luyện viên của mỗi đội cần trình với trọng tài một danh sách sắp thứ tự 5 cầu thủ trong số 11 cầu thủ để đá luân lưu 5 quả 11 mét.
Mỗi danh sách có xếp thứ tự 5 cầu thủ được gọi là một chỉnh hợp chập 5 của 11 cầu thủ.
Kí hiệu số chỉnh hợp chập của phần tử là .
Số chỉnh hợp chập của phần tử được tính bởi công thức
.
với và .
¶ Hoán vị không lặp
Mỗi một chỉnh hợp chập của phần tử là một hoán vị của phần tử đó.
Kí hiệu số hoán vị của phần tử là .
Số hoán vị của được tính bởi công thức:
.
¶ Hoán vị lặp (Permutation with Repetition)
Hoán vị trong đó mỗi phần tử xuất hiện ít nhất một lần được gọi là hoán vị lặp.
Số hoán vị lặp của phần tử thuộc loại, mà các phần tử loại () xuất hiện lần được kí hiệu là và được tính bằng công thức
¶ Các đối tượng tổ hợp (Combinatorial Objects)
Một song ánh (bijection) là tương ứng một-một giữa hai tập hợp, ví dụ tập hợp những người chồng và tập hợp những người vợ (một chồng chỉ có một vợ, và một vợ chỉ có đúng một chồng). Do đó, nếu bạn biết được lực lượng của một tập hợp, bạn có thể biết được lực lượng của tập kia. Ta có thể sử dụng tính chất này trong nhiều bài toán Tổ hợp, đặc biệt là các bài toán đếm, nhưng trước tiên, ta phải biết tính lực lượng của một tập các đối tượng tổ hợp.
¶ Tổ hợp không lặp (Combinations without repetition)
Trong tổ hợp, ta thường phải chọn một tập các phần tử nào đó và không quan tâm đến thứ tự của chúng. Số lượng tập con phần tử của một tập phần tử (còn gọi là số tổ hợp chập của phần tử) là:
¶ Tổ hợp có lặp (Combinations with repetition)
Giả sử ta cần chọn phần tử từ một tập phần tử, không quan trọng thứ tự và một phần tử có thể được chọn nhiều lần. Khi đó, số cách chọn là số tổ hợp lặp chập của phần tử và có giá trị là:
Một tính chất thú vị về số tổ hợp có lặp: là số nghiệm nguyên không âm của phương trình: với là hằng số nguyên dương.
¶ Vector nhị phân (Binary Vectors)
Vector nhị phân là kiểu dữ liệu <bitset> trong C++ STL.
Ngoài ra, các tính chất về tổ hợp của vector nhị phân cũng rất quan trọng. Sau đây là một số tính chất hay được sử dụng của vector nhị phân.
-
Số lượng vector nhị phân độ dài là .
-
Số lượng vector nhị phân độ dài có số 1 là , vì ta chọn vị trí có số 1 trong vị trí.
-
Số lượng cặp vector nhị phân (có quan tâm đến thứ tự) thỏa mãn điều kiện khoảng cách giữa và là là .
Khoảng cách giữa hai vector nhị phân và là số lượng giá trị nguyên không âm thỏa mãn
¶ Hệ thức truy hồi (Recurrence Relations)
Hệ thức truy hồi là công cụ hỗ trợ đắc lực trong các bài toán đếm. Truy hồi còn giúp ta định nghĩa được nhiều cấu trúc như cây, danh sách, công thức quy hoạch động hay các thuật toán "chia để trị", nên truy hồi được sử dụng rất nhiều trong tin học.
Hệ thức truy hồi là một phương trình dùng để xác định dãy số hoặc hàm số bằng cách dùng các số hạng trước để định nghĩa số hạng sau. Nó rất hữu dụng vì nhiều dãy số có thể dễ dàng được định nghĩa bằng hệ thức truy hồi:
-
Hàm đa thức (Polynomials): .
-
Hàm mũ (Exponentials): .
-
Giai thừa: .
Ta thường dễ dàng tìm được hệ thức truy hồi để giải các bài toán đếm. Giải hệ thức truy hồi để có được dạng công thức cần tìm là cả một nghệ thuật, tuy vậy ta có thể sử dụng trực tiếp hệ thức truy hồi để giải một số bài toán đơn giản.
¶ Hệ số nhị thức (Binomial Coefficients)
Hệ số nhị thức được sử dụng để đếm số cách chọn vật trong số vật.
¶ Đếm số đường đi trên lưới (Paths Across a Grid)
Có bao nhiêu cách để đi từ góc trái trên của một bảng ô đến góc phải dưới của ô đó, nếu ta chỉ được phép đi về bên phải hoặc đi xuống dưới. Ta thấy mọi đường đi hợp lệ có bước, và hai đường đi khác nhau nếu và chỉ nếu chúng có một bước đi xuống dưới khác nhau, vậy ta có cách đi.
Tính hệ số nhị thức có thể gây tràn số ở các bước trung gian, vì vậy ta nên tính hệ số nhị thức bằng công thức:
/*
Sử dụng công thức truy hồi:
nCr = (n-1)Cr + (n-1)C(r-1)
ta dễ dàng khởi tạo tất cả các giá trị nCr trong O(N^2).
Code có thể chạy được với n <= 5000 và mod bất kỳ (không cần nguyên tố).
*/
//by Tanmay Chaudhari
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
long long ncr[5005][5005];
void precompute()
{
int k;
for (int i = 0; i < 5001; i++)
{
ncr[i][0] = ncr[i][i] = 1;
k = i >> 1;
for (int j = 1; j < k + 1; j++)
ncr[i][j] = ncr[i][i - j] = (ncr[i - 1][j] + ncr[i - 1][j - 1]) % MOD;
}
}
int main()
{
precompute();
cout << ncr[4892][231] << endl;
return 0;
}
Chương trình trên chỉ tính được với nhỏ. Bạn có thể tham khảo chương trình sau để tính với là một số nguyên tố và lớn.
Chú ý: Code sau sử dụng nghịch đảo modulo, đã được giới thiệu ở bài viết Số học 4.5
/*
Tính nCr trong O(N) với mod P nguyên tố.
Ta sử dụng công thức nCr = n! / r! / (n-r)!
Khởi tạo trước fac[i] = i! mod P
Khởi tạo trước ifac[i] = i!^-1 mod P (nghịch đảo modulo P của i!).
Từ đó dễ dàng tính được nCr trong O(1).
*/
//by Tanmay Chaudhari
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
#define N 2123456
#define LL long long
LL fac[N], ifac[N];
LL PowerMod(LL a, LL n){
LL ret = 1;
while (n){
if (n & 1){
ret *= a;
ret %= MOD;
}
a *= a;
a %= MOD;
n /= 2;
}
return ret;
}
inline void precompute(){
int i;
fac[0] = 1;
for (i = 1; i < N; i++){
fac[i] = (i * fac[i - 1]) % MOD;
}
ifac[N - 1] = PowerMod(fac[N - 1], MOD - 2);
for (i = N - 2; i >= 0; i--){
ifac[i] = ((i + 1) * ifac[i + 1]) % MOD;
}
}
LL com(int n, int r){
LL ret = fac[n];
ret *= ifac[r];
ret %= MOD;
ret *= ifac[n - r];
ret %= MOD;
return ret;
}
int main()
{
precompute();
cout << com(4892,231) << endl;
return 0;
}
¶ Một vài dãy số cơ bản (Counting Sequences)
¶ Dãy số Catalan
Định nghĩa:
Các ứng dụng của dãy số Catalan:
-
Cho một đa giác lồi đỉnh, ta chia đa giác thành các tam giác bằng cách vẽ các đường chéo không cắt nhau trong đa giác. là số cách chia như vậy.
-
là số các từ Dyck có độ dài . Từ Dyck là từ gồm chữ X và chữ Y sao cho với mọi tiền tố của từ đó, số lượng chữ X không ít hơn số lượng chữ Y. Ví dụ, từ sau đây là từ Dyck độ dài 6: XXXYYY, XYXXYY, XYXYXY, XXYYXY, XXYXYY.
-
Thay mỗi chữ X trong từ Dyck thành dấu mở ngoặc đơn, mỗi chữ Y thành dấu đóng ngoặc đơn, khi đó mỗi từ Dyck trở thành một dãy ngoặc hợp lệ. Vậy còn đếm số dãy ngoặc hợp lệ gồm cặp ngoặc: ((())), ()(()), ()()(), (())(), (()()).
-
còn là số cách đặt ngoặc cho một biểu thức gồm thừa số. Ví dụ với , ta có 5 cách đặt ngoặc cho 4 thừa số: .
-
còn là số cây nhị phân đầy đủ có là (một cây nhị phân được gọi là đầy đủ nếu mọi nút của nó có hai nút con hoặc không có nút con nào).

¶ Số Euler
Số Euler là số lượng hoán vị các số từ 1 đến mà có đúng phần tử lớn hơn phần tử đứng trước nó. Hệ thức truy hồi tính số Euler được lập bằng cách xét mỗi hoán vị của 1,2,...,. Có vị trí để thêm số vào hoán vị, và một cách thêm số có thể làm tăng số phần tử lớn hơn phần tử đứng trước nó của , hoặc bảo toàn số phần tử lớn hơn phần tử đứng trước nó. Vì vậy,
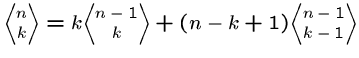
¶ Bài toán phân tích một số nguyên (Integer Partitions)
Ta xét bài toán sau:
Cho một số nguyên . Hãy cho biết có bao nhiêu cách phân tích số thành tổng của dãy các số nguyên dương, các cách phân tích là hoán vị của nhau chỉ tính là một cách.
Ví dụ: có 7 cách phân tích:
Cách dễ nhất để đếm số cách phân tích số là định nghĩa hàm là số cách phân tích số thành tổng của các số nguyên dương nhỏ hơn hoặc bằng . Các cách phân tích số thành tổng cách số nguyên dương nhỏ hơn hoặc bằng có thể chia làm hai loại: chứa số trong phép phân tích và không chứa số trong phép phân tích, vì thế ta có . Ngoài ra, ta còn dễ dàng có được và với .