¶ Bao hàm - Loại trừ (Inclusion-Exclusion)
Nguồn: HackerEarth
Người dịch: Bùi Việt Dũng
¶ Bao hàm - loại trừ (Inclusion-Exclusion)
¶ Phát biểu công thức
Công thức bao hàm - loại trừ được phát biểu như sau:
Để tính lực lượng của hợp của nhiều tập hợp, ta tính tổng lực lượng các tập hợp đó, rồi trừ đi lực lượng của giao của các cặp hai tập hợp khác nhau, rồi cộng lực lượng của giao các bộ ba tập hợp khác nhau, rồi trừ đi lực lượng của các bộ bốn tập hợp, và cứ thế cho đến khi ta xét đến giao của tất cả các tập hợp.
¶ Công thức dành cho tập hợp
Công thức bao hàm - loại trừ có dạng như sau:
Ta có thể viết công thức này một cách gọn hơn bằng cách tính tổng của các tập con. Gọi là tập hợp các tập hợp . Khi đó công thức bao hàm - loại trừ có dạng:
¶ Lập công thức bằng biểu đồ Venn (Venn diagrams)
Ta có biểu đồ sau biểu diễn ba tập hợp , và .
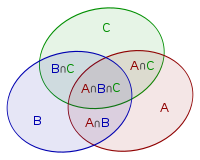
Khi đó ta thấy lực lượng của bằng lực lượng của , , trừ đi lực lượng của , , rồi cộng thêm lực lượng của .
Tương tự, ta có thể lập công thức với tập hợp.
¶ Công thức dành cho xác suất
Nếu ta có biến cố , là xác suất của biến cố , xác suất của biến cố hợp của chúng (nghĩa là biến cố "có ít nhất một trong số biến cố xảy ra") là
Nếu gọi là tập hợp các tập hợp , công thức này cũng có thể viết gọn như sau:
¶ Chứng minh công thức bao hàm - loại trừ
Để thuật tiện trong chứng minh, ta sử dụng công thức viết gọn sau:
với là tập hợp các tập hợp .
Ta cần chứng minh một phần tử bất kì thuộc ít nhất một tập , sẽ chỉ được đếm một lần trong công thức.
Xét một phần tử bất kì thuộc tập hợp . Ta thấy
-
Trong công thức, khi , được đếm thêm lần.
-
Trong công thức, khi , được đếm bớt đi lần bởi bị đếm bớt đi khi ta xét một cặp 2 tập hợp khác nhau trong số tập hợp chứa phần tử .
-
Trong công thức, khi , được đếm thêm lần.
-
...
-
Trong công thức, khi , được đếm lần. Nếu lẻ thì được đếm thêm, nếu chẵn thì được đếm bớt.
-
Trong công thức, khi , không được đếm.
Vì vậy, số lần được đếm là .
Để tính , ta khai triển bằng nhị thức Niu-tơn (Newton binomial):
.
Ta thấy với , , do đó hay điều phải chứng minh.
¶ Ứng dụng: Đếm số số nguyên tố cùng nhau với một số cho trước trong một đoạn
Đây là một bài toán dễ dựa trên công thức bao hàm - loại trừ.
Cho hai số nguyên và , đếm số số nguyên tố cùng nhau với trong đoạn .
Thuật toán: Tìm phần bù (the inverse): Đếm số số không nguyên tố cùng nhau với .
Xét các ước nguyên tố của , đánh số chúng từ 1 đến .
Ta có thể tính số số trong đoạn chia hết cho bằng công thức .
Tuy vậy, nếu ta chỉ tính tổng tất cả các số này, ta sẽ ra kết qủa sai. Đó là do một số số có thể chia hết cho nhiều . Vì vậy ta cần sử dụng đến công thức bao hàm - loại trừ.
int solve (int n, int r) {
int sum = 0;
vector<int> p;
for (int i=2; i*i<=n; ++i)
if (n % i == 0) {
p.push_back (i);
while (n % i == 0) n /= i;
}
if (n > 1) p.push_back (n);
for (int msk=1; msk<(1<<p.size()); ++msk) {
int mult = 1, bits = 0;
for (int i=0; i<(int)p.size(); ++i)
if (msk & (1<<i)) {
++bits;
mult *= p[i];
}
int cur = r / mult;
if (bits % 2 == 1) sum += cur;
else sum -= cur;
}
return r - sum;
}