¶ "Nhảy nhị phân" với bộ nhớ
Người viết: Ngô Nhật Quang - Trường THPT Chuyên Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
¶ Giới thiệu
Trước khi đọc bài viết bài, người viết giả dụ bạn đọc đã đọc và hiểu về binary lifting (Nâng nhị phân).
Bài viết này sẽ giới thiệu một thuật toán được công bố năm 1983 bởi tiến sĩ Eugene W. Myers. Như thuật toán binary lifting đã được giới thiệu trước trên VNOI Wiki, thuật toán giới thiệu trong bài này cũng có độ phức tạp truy vấn là . Tuy nhiên, với thuật toán này, ta có thể thêm hoặc bớt một lá trong cây trong , tức tổng bộ nhớ cần thiết chỉ là thay vì .
Lưu ý: Các đoạn code mẫu chỉ dùng để tham khảo chứ không thể biên dịch, ban đọc có thể tham khảo code trong phần Thử nghiệm thời gian chạy.
¶ Cấu trúc
Cơ bản nhất, cấu trúc cây được cài đặt như sau với ba biến cho mỗi đỉnh trên cây:
class Node {
int depth;
Node parent;
Node jump;
}
Chức năng của id, depth và parent ta có thể đoán được qua tên. Biến id lưu trữ số thứ tự của đỉnh này, depth sẽ lưu trữ độ sâu của đỉnh này, còn biến parent sẽ là con trỏ trỏ đến cha của đỉnh này. Biến jump lúc này ta sẽ "tạm" định nghĩa nó là một con trỏ trỏ đến một đỉnh tổ tiên bất kì. Ta sẽ đi sâu hơn việc cài đặt biến jump ở phần sau. Biến root sẽ là gốc của cây.
Với đỉnh là đỉnh gốc của cây, ta định nghĩa
root.parent = null;
root.depth = 0;
root.jump = root;
¶ Binary Lifting
Với định nghĩa trên, ta đã có thể dựng ra một đoạn code để tìm tổ tiên có độ sâu là của của đỉnh .
Node find(Node u, int d) {
// Lặp đến khi độ sâu đỉnh hiện tại là d
while (u.depth > d) {
// Nếu đỉnh jump có độ sâu
// bé hơn d thì ta chỉ nhảy lên cha
if (u.jump.depth < d) {
u = u.parent;
}
else {
// Còn không ta sẽ nhảy lên qua con trỏ jump
u = u.jump;
}
}
return u;
}
Đoạn code khá đơn giản vì ta cũng khó làm được gì nhiều với hai con trỏ lên trên. Ta sẽ đi lên trên bằng cách "nhảy" liên tục lên đỉnh jump mà kiểm tra rằng ta không nhảy quá đỉnh mà ta đang cần tìm.
¶ Định nghĩa con trỏ jump
Rõ ràng, với đoạn code như trên, ta đến được đỉnh cần tìm hoàn toàn phụ thuộc vào việc các biến jump đưa ta đến đỉnh cần tìm nhanh như nào. Hàm thêm một lá vào cây trông như sau:
Node makeLeaf(Node p) {
Node leaf = new Node();
leaf.parent = p;
leaf.depth = p.depth + 1;
if (p.depth - p.jump.depth == p.jump.depth - p.jump.jump.depth) {
leaf.jump = p.jump.jump;
}
else {
leaf.jump = p;
}
return leaf;
}
Phần gán biến id, parent và depth khá dễ hiểu, nhưng còn đoạn này thì nghĩa là gì?
p.depth - p.jump.depth == p.jump.depth - p.jump.jump.depth
Chứng minh tính đúng đắn của nó khá dài, bạn đọc muốn tìm hiểu có thể đọc bài nghiên cứu của tiến sĩ Myers có tên là "An applicative random-access stack".
Dưới đây sẽ là một số hình ảnh để bạn đọc có thể có một số ý tưởng tại sao nó lại đúng.
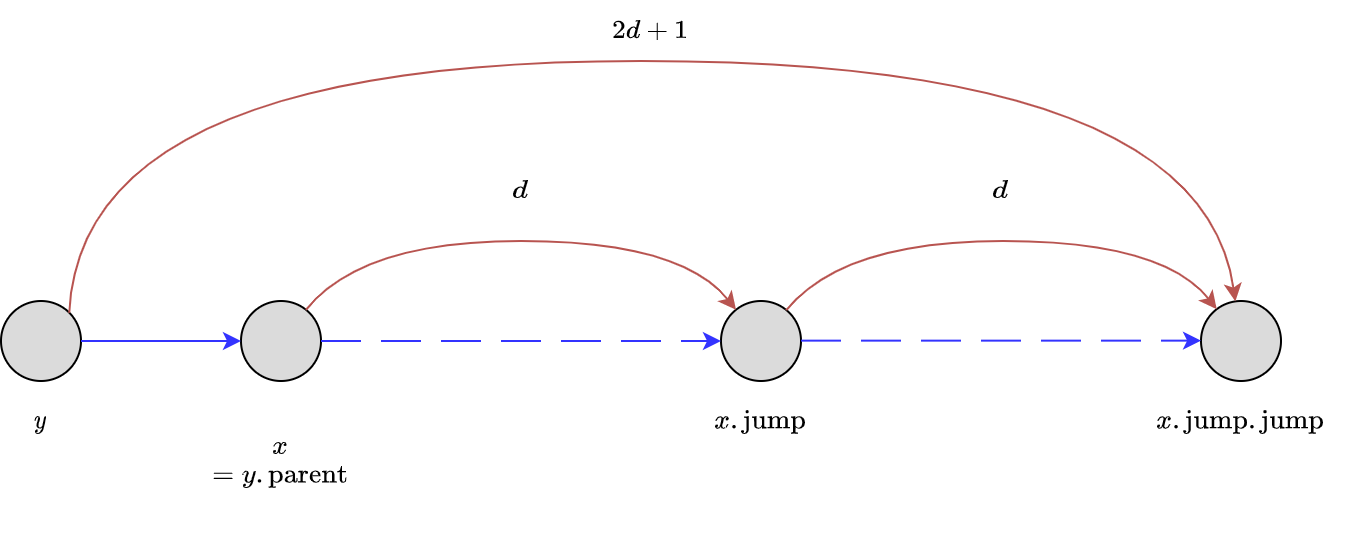
Ở đây, đỉnh y là lá ta vừa thêm vào cây. Các mũi tên màu đỏ thể hiện các cú nhảy qua con trỏ jump, còn mũi tên màu xanh là đi lên cha nó qua con trỏ parent. Dễ thấy khi xem lại hàm find của ta, nó sẽ thử nhảy bước , nếu không được thì sẽ nhảy lên đỉnh cha. Bước nhảy ở đỉnh cha sẽ luôn luôn ngắn hơn bước nhảy của đỉnh con, ngắn hơn ít nhất lần.
Nhớ lại, đây không phải giống hệt binary lifting mà ta biết hay sao? Chỉ là thay vì nhồi bước nhảy vào trong một đỉnh, ta dàn đều nó ra khắp các đỉnh tổ tiên của nó.
Điều này giúp ta giải thích việc ta luôn tìm được đỉnh có bước nhảy bé hơn nhanh. Thế nếu ta ở một đỉnh rất sâu, mà nó lại không có bước nhảy đủ to thì sao? Vậy thì việc có bước nhảy bé hơn thì có tác dụng gì? Ta nhìn vào bức ảnh lớn hơn:
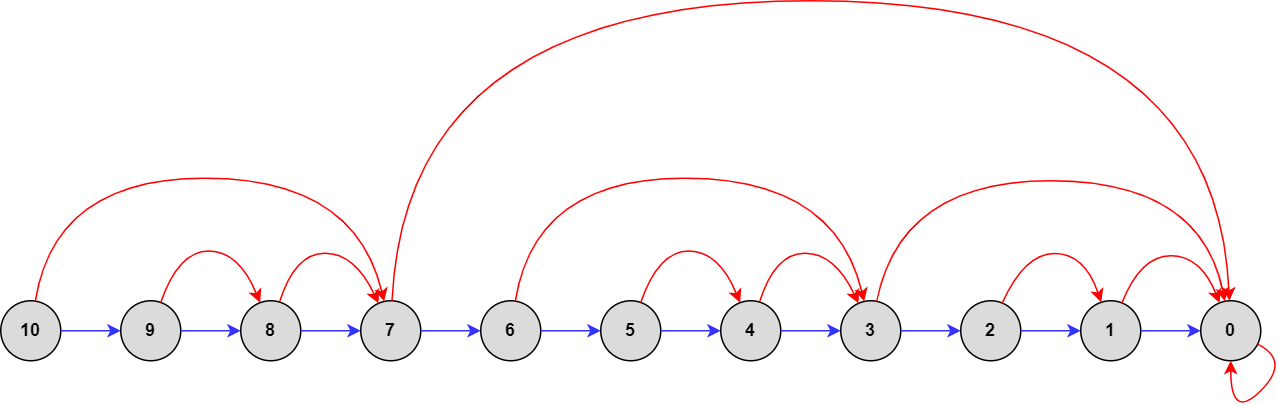
Bức ảnh không lớn lắm, nhưng mong bạn đọc có thể nhận ra bức tranh tổng thể mà thuật toán muốn thực hiện. Nhận thấy rằng sau tối đa hai bước nhảy qua con trỏ jump, ta sẽ đến được một đỉnh có bước nhảy lớn hơn ít nhất gấp đôi. Tức là, nếu ta cứ nhảy qua con trỏ jump liên tục, độ dài của bước nhảy sẽ tăng theo cấp số nhân.
Qua hai bức ảnh này, ta có thể phần nào đó nhận ra cách mà hàm find hoạt động:
- Tăng tốc (tìm bước nhảy lớn hơn) bằng cách nhảy liên tục
- Giảm tốc (tìm bước nhảy ngắn hơn) bằng cách sử dụng bước nhảy của cha nó.
Rõ ràng, lúc này ta có thể thấy ta không thể đảm bảo sử dụng tối đa bước nhảy để đến đích. Bài nghiên cứu của tiến sĩ Myers cho ta cận trên với là độ sâu của đỉnh khởi đầu.
¶ Thử nghiệm thời gian chạy
Như phần trước, ta có được cận trên của thuật toán là sử dụng . Vậy có nghĩa là thực tế code ta sẽ chạy lâu gấp lần code binary lifting bình thường đúng không?
Nếu đúng thì đã không có phần này. Ta xem các submission sau đây:
| Link bài | Bộ nhớ | Bộ nhớ |
|---|---|---|
| VNOJ - Sloth Naptime | 441ms | 1265ms |
| Codeforces - Minimum spanning tree for each edge | 265 ms | 358 ms |
| Library Checker - Lowest Common Ancestor | 436 ms | 664 ms |
Điều này cho ta thấy, ít nhất là trên các bộ test ngẫu nhiên, thì binary lifting bộ nhớ chạy nhanh hơn, thậm chí là nhanh gấp đôi, gấp ba lần. Theo suy đoán của tác giả, điều này liên quan đến cách sử dụng bộ nhớ đệm của mỗi thuật toán. Bạn đọc muốn tìm hiểu thêm có ở đọc tại đây. Đây cũng là lí do mà tại sao quy hoạch động cuốn chiếu không chỉ dùng ít bộ nhớ hơn mà còn thường chạy nhanh hơn quy hoạch động thông thường.
¶ Tìm tổ tiên chung sâu nhất của hai đỉnh
Như cách ta định nghĩa con trỏ jump như trên, ta có thể thấy rằng với hai đỉnh bất kì với cùng độ sâu, thì hai đỉnh jump của chúng cũng sẽ có độ sâu giống nhau. Do vậy, giả dụ hai đỉnh được cho là và và đỉnh sâu hơn là , thì ta tìm đỉnh là tổ tiên của đỉnh có độ sâu bằng đỉnh . Sau đó, ta nhảy lên dần dần ở cả hai đỉnh cho đến khi chúng giống nhau.
Node lca(Node u, Node v) {
if (u.depth < v.depth) swap(u, v);
u = find(u, v.depth);
while (u != v) {
if (u.jump == v.jump) {
u = u.parent;
v = v.parent;
}
else {
u = u.jump;
v = v.jump;
}
}
return u;
}
¶ Tham khảo
- "Binary Lifting, No Memory Wasted" - Urbanowicz