¶ Áp dụng bất ngờ của đạo hàm
Người viết: Nguyễn Thành Trung - Singapore
Lúc học môn Toán có lẽ chúng ta thường hay tự hỏi: Học đạo hàm, tích phân.. để làm gì? Hôm nay chúng ta sẽ cùng nghiên cứu một áp dụng vô cùng bất ngờ và ảo ma của đạo hàm trong 1 bài toán.
Bài toán như sau:
- Cho ngôi nhà trên 1 đường thẳng. Ngôi nhà thứ có tầng.
- Để khu phố nhìn đẹp hơn, người ta muốn sửa lại các ngôi nhà sao cho độ cao của tất cả các ngôi nhà đều bằng nhau, bằng cách xây thêm hoặc đập đi một số tầng của một số ngôi nhà.
- Với ngôi nhà thứ , chi phí để xây thêm 1 tầng hoặc đập đi 1 tầng là .
- Tìm chi phí nhỏ nhất.
- Giới hạn: , , .
Ví dụ: với , , . Cách tối ưu là đưa cả 3 nhà về độ cao , với chi phí:
Các bạn có thể đọc đề và nộp thử tại SPOJ (tuy nhiên giới hạn trong bài SPOJ này khá nhỏ).
¶ Lời giải
Đầu tiên chúng ta hãy nghiên cứu 1 số lời giải "thông thường" cho bài toán này.
Đặt là chi phí để sửa ngôi nhà thứ về độ cao . Ta có công thức:
Đặt , nói cách khác là chi phí để đưa tất cả các ngôi nhà về độ cao . Đề bài yêu cầu ta tìm .
¶ Nhận xét 1:
Đặt là giá trị của để hàm đạt giá trị nhỏ nhất, khi đó:
Khá hiển nhiên, giả sử , điều này chỉ xảy ra khi ta phải giảm độ cao của tất cả các ngôi nhà đi ít nhất 1 tầng. Với mỗi ngôi nhà ta giảm nó ít đi 1 tầng thì sẽ được chi phí nhỏ hơn. Do đó .
Tương tự, ta cũng chứng minh được
Với nhận xét này, ta có thuật toán , với là giá trị lớn nhất của : duyệt tất cả các giá trị của , với mỗi , ta tính hàm trong .
¶ Nhận xét 2:
Hàm là tổng của các hàm lồi (strictly convex) nên nó cũng là hàm lồi.
Ví dụ: trong ảnh mình vẽ hàm màu đỏ là tổng của 3 hàm , và . Có thể thấy là hàm lồi
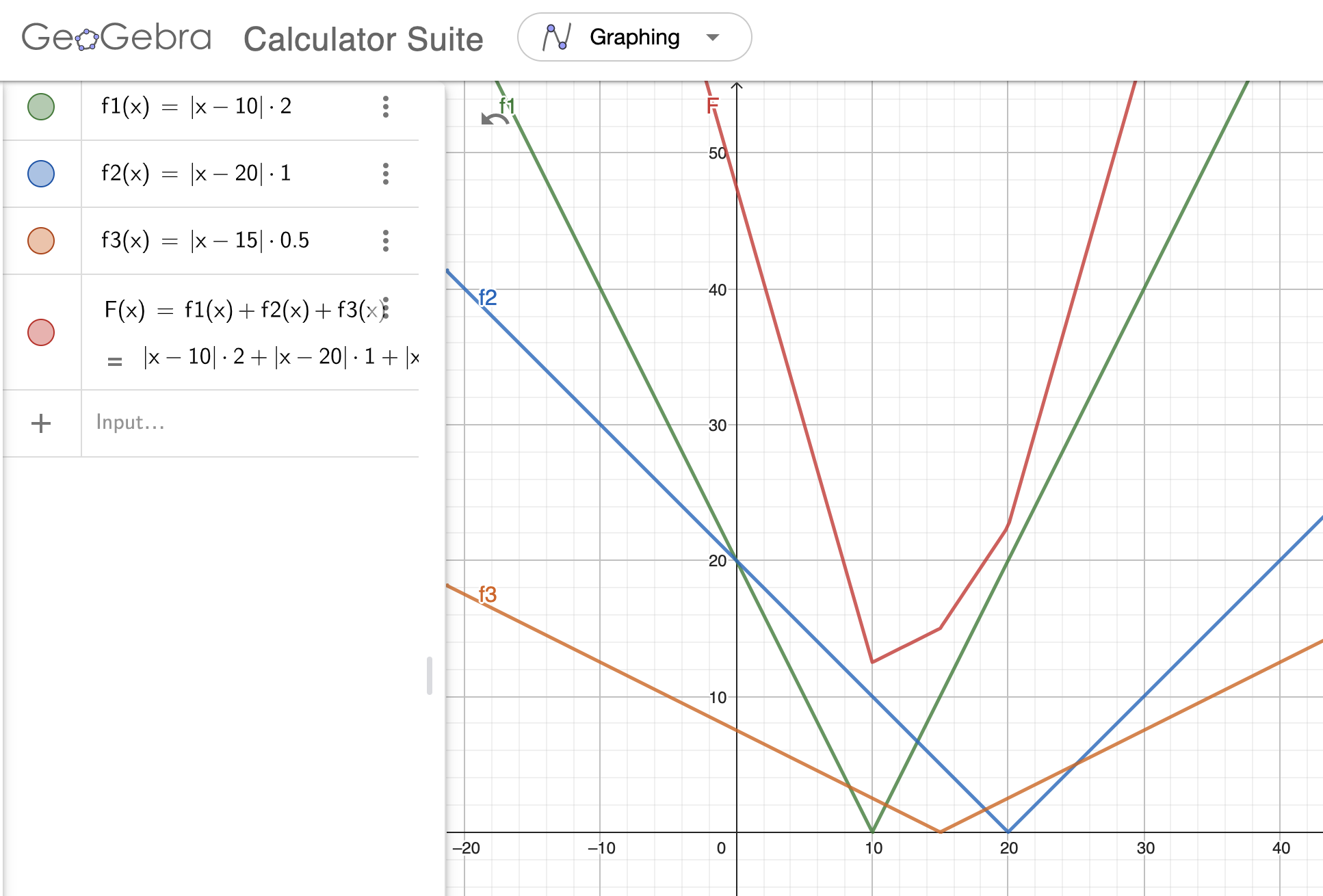
Do đó ta có thể sử dụng tìm kiếm tam phân để tìm giá trị nhỏ nhất của .
đến đây ta đã có thuật toán với độ phức tạp .
¶ Lời giải
Rất bất ngờ, bài này còn có thể giải được với độ phức tạp sử dụng đạo hàm!
Ở bài viết này chúng ta ứng dụng đạo hàm của hàm trên số nguyên ( với chỉ nhận giá trị nguyên) - discrete derivative. Định nghĩa:
Áp dụng công thức trên vào bài toán ban đầu: ta tính đạo hàm của hàm chi phí:
.
Cũng theo tính chất của đạo hàm:
Ví dụ: hàm màu tím là đạo hàm của hàm màu xanh
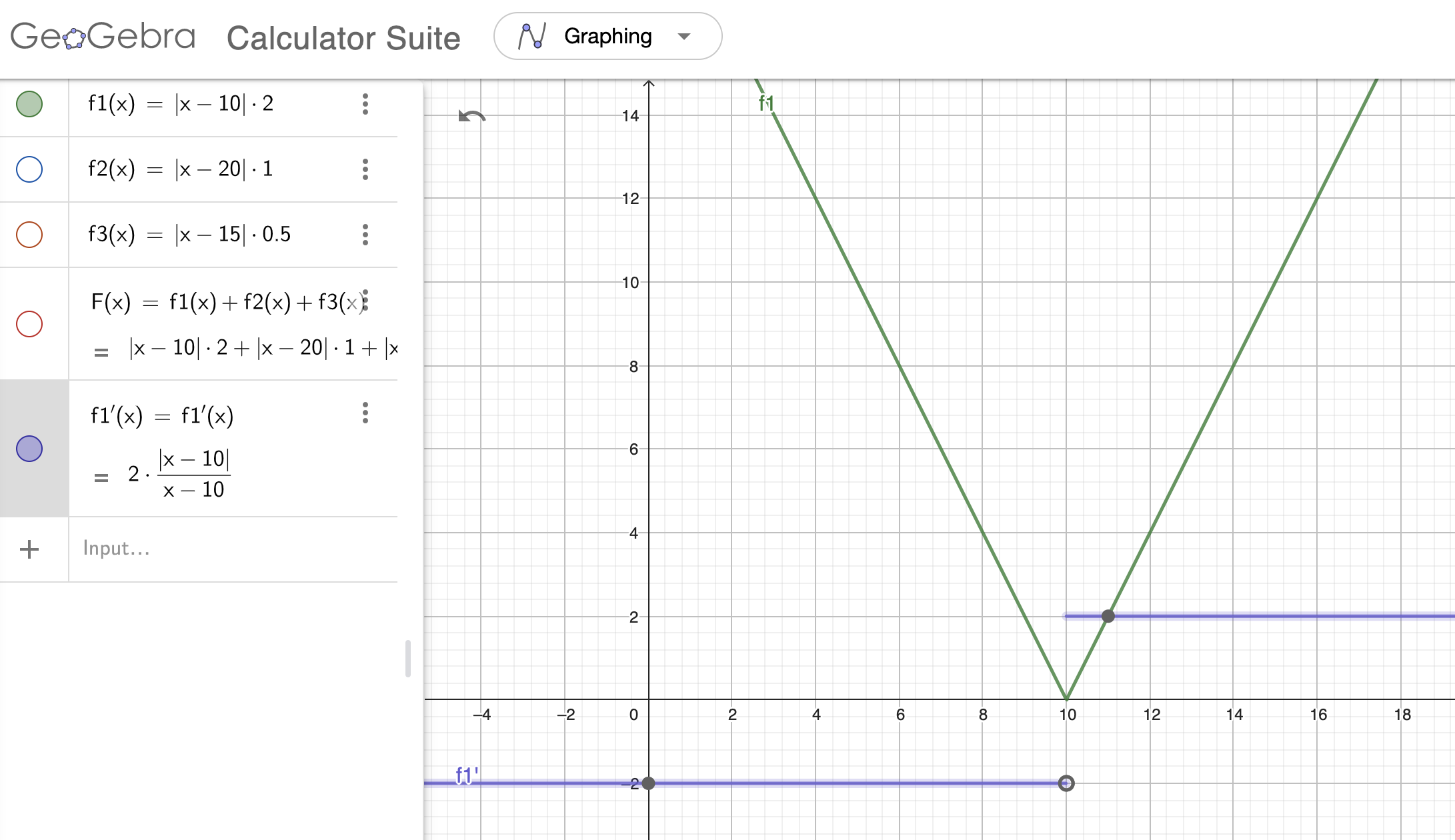
Ta tính đạo hàm thêm lần nữa:
nếu , ngược lại .
Cũng theo tính chất của đạo hàm:
Hàm chính là mấu chốt để giải bài toán này: hàm chỉ khác tại đúng 1 điểm, do đó ta dễ dàng "tính" được trong .
ta có thể tính được trong rất đơn giản như sau:
vector<int> F2(MAX_H + 1); // F2[x] = F''(x)
for (int i = 0; i < N; ++i) {
// f''i(x) = 2*C(i) at x = H(i)+1
F2[H[i] + 1] += 2 * C[i];
}
Dựa vào định nghĩa của đạo hàm (), từ ta có thể dễ dàng tính được trong :
vector<int> F1(MAX_H + 1); // F1[x] = F'(x)
// Tính F'(0)
for (int i = 0; i < N; ++i) {
F1[0] -= C[i];
}
// Tính F'(x)
for (int x = 1; x <= MAX_H; ++x) {
F1[x] = F1[x-1] + F2[x];
}
Tương tự, ta có thể tính được trong :
vector<int> F(MAX_H + 1);
// Tính F(0)
for (int i = 0; i < N; ++i) {
F[0] += H[i] * C[i];
}
// Tính F(x)
for (int x = 1; x <= MAX_H; ++x) {
F[x] = F[x-1] + F1[x];
}
Đến đây ta đã thu được thuật toán với độ phức tạp !
¶ Bonus
Sử dụng đạo hàm, ta cũng có thể chứng minh hàm là hàm lồi, và do đó cách chặt tam phân trình bày ở trên là chính xác.
Một hàm số là hàm lồi trong đoạn nếu đạo hàm bậc 2 của nó luôn lớn hơn hoặc bằng trong khoảng . (Một cách hiểu trực quan: có thể thấy nếu đạo hàm bậc 2 không âm đạo hàm bậc 1 là hàm tăng dần hàm số luôn "cong cong" về phía trên). (Xem thêm trên trang Wiki về hàm lồi)
Ở bài này, dễ thấy luôn lớn hơn hoặc bằng , do đó cũng luôn lớn hơn hoặc bằng .
Hình vẽ chụp từ Geogebra: https://www.geogebra.org/calculator/pcyur4yk