¶ Shortest Path DAG và ứng dụng
Người viết: Nguyễn Đăng Quân - Đại học Công nghệ, Đại học Quốc gia Hà Nội
Trong một số bài toán liên quan đến đường đi ngắn nhất, tính chất của đồ thị khá khó nhận ra và cũng không dễ dàng để áp dụng. Hôm nay mình xin chia sẻ các bạn một kĩ thuật sử dụng phương pháp tính toán trên DAG (Directed Acyclic Graph) để giải một số bài toán về đường đi ngắn nhất.
¶ Bài toán mở đầu
¶ Đếm số đường đi trên DAG
Cho đồ thị có hướng không chu trình gồm đỉnh và cung. Với mỗi đỉnh, hãy đếm số đường đi từ tới đỉnh đó trên đồ thị.
¶ Thuật toán
Bài toán trên khá quen thuộc với đa số mọi người, cách giải là sử dụng qui hoạch động trên Thứ tự topo:
- Đầu tiên, các bạn sắp xếp các đỉnh theo thứ tự Topo: .
- Gọi là số lượng đường đi từ tới trên đồ thị, ta có:
- .
- với mọi cung trên đồ thị.
Code mẫu:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e5 + 5;
// adj[u]: Lưu các đỉnh v mà có cung u->v, nếu có nhiều cung u->v thì lưu đỉnh v nhiều lần
int n, m;
vector < int > adj[N];
int nTopo, v[N];
bool vis[N];
int f[N];
void dfs(int u) {
vis[u] = true;
for (auto i: adj[u])
if (!vis[i])
dfs(i);
v[++nTopo] = u;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
int u, v;
cin >> u >> v;
adj[u].emplace_back(v);
}
/* Sắp xếp topo */
for (int i = 1; i <= n; ++i)
if (!vis[i])
dfs(i);
// Sau khi dfs xong, ta được thứ tự trong v là thứ tự ngược topo
reverse(v + 1, v + nTopo + 1);
f[1] = 1;
/* Qui hoạch động trên DAG */
for (int i = 1; i <= n; ++i)
for (auto j: adj[v[i]])
f[j] += f[v[i]];
// In đáp án
for (int i = 1; i <= n; ++i)
cout << f[i] << " ";
}
Khi đó, độ phức tạp của thuật toán là , bởi thao tác sắp xếp Topo và thao tác tính hàm mục tiêu đều tốn thời gian .
¶ Bài toán đếm số đường đi ngắn nhất
Cho đồ thị vô hướng không chu trình gồm đỉnh và cạnh có trọng số dương. Với mỗi đỉnh, hãy đếm số đường đi ngắn nhất từ tới đỉnh đó trên đồ thị.
Link bài tập gốc: https://vjudge.net/problem/Gym-406204J
¶ Hướng tiếp cận
Trước tiên; để đếm được số đường đi ngắn nhất, ta cần phải nắm được cách tìm giá trị đường đi đó. Mình xin phép không nhắc lại các thuật toán tìm kiếm đường đi ngắn nhất; nếu bạn chưa biết hoặc biết nhưng đã quên thì có thể đọc lại trên VNOI wiki.
Trong bài toán này, ta sẽ gọi:
- là độ dài đường đi ngắn nhất từ đỉnh tới đỉnh trên đồ thị.
- là số đường đi ngắn nhất từ đỉnh tới đỉnh .
Vậy tại sao phải tính được trước độ dài đường đi ngắn nhất?
Định hướng lại đồ thị như sau:
- Giữ nguyên các đỉnh
- Với mỗi cạnh
- Nếu , cạnh này sẽ biến thành cung .
- Nếu , cạnh này sẽ biến thành cung .
- Nếu hai điều kiện trên không thỏa mãn, cạnh này bị xóa bỏ khỏi đồ thị.
Ví dụ:
- Đồ thị ban đầu:
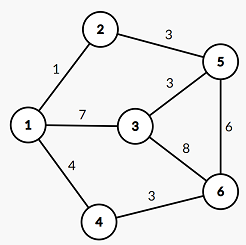
- Đồ thị đã thay đổi:
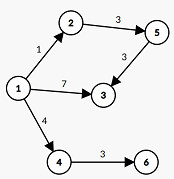
Khi đó, chính là số đường đi từ đến . Bài toán này trở thành bài Đếm số đường đi trên DAG.
Để hiểu rõ hơn, các bạn hãy theo dõi phần tiếp theo.
¶ Shortest Path DAG
Cho một đồ thị vô hướng . Gọi là độ dài đường đi ngắn nhất từ đến (Nếu không tồn tại đường đi thì ).
Ta dựng ra một đồ thị có hướng như sau:
- Mỗi đỉnh trong đồ thị sẽ ứng với một đỉnh trong .
- Mỗi cạnh sẽ biến đổi như sau:
- Nếu thì dựng ra cung trong .
- Nếu thì dựng ra cung trong .
Khi đó, ta gọi đồ thị là Shortest Path DAG ứng với đỉnh trên .
¶ Tính chất
Đồ thị có một số tính chất khá đặc biệt như sau:
- Nếu tồn tại đường đi từ đến trên (Tức là ) thì cũng tồn tại đường đi (có hướng) từ đến trên
Đây là một nhận xét hiển nhiên, bạn đọc có thể tự suy ngẫm về tính đúng.
- Mọi đường đi trên đều là đường đi ngắn nhất trên .
Chứng minh:
Gọi là độ dài đường đi dài nhất từ đến trên (Nếu không tồn tại thì ). Điều kiện trên tương đương với một trong hai điều kiện sau thỏa mãn:
- (Không tồn tại đường đi)
- (Nếu tồn tại đường đi thì đó phải là đường đi ngắn nhất)
Trước tiên, ta chứng minh đường đi xuất phát từ đỉnh đều là đường đi ngắn nhất.
Giả sử nhận xét trên là sai, tức là tồn tại một đỉnh và đường đi mà .
Theo đó:
Điều ta giả sử là sai, dẫn đến
Nếu tồn tại đường đi từ đến , ta biết ; do đó tồn tại đường đi từ đến và .
Mặt khác, theo bất đẳng thức tam giác:
hay
suy ra
Dấu bằng phải xảy ra, hay .
Ta hoàn tất chứng minh.
- là đồ thị có hướng không chu trình (DAG)
Chứng minh:
Nếu đồ thị có chu trình chứa một đỉnh nào đó, ta có do trọng số các cạnh là dương, dẫn đến mâu thuẫn.
- Nếu tồn tại đường đi từ đến trên thì mọi đường đi ngắn nhất từ đến sẽ đều xuất hiện trong .
Chứng minh:
Vì tồn tại một đường đi từ đến trên nên theo tính chất 2:
Xét một đường đi ngắn nhất từ đến không xuất hiện trong đồ thị:
Theo bất đẳng thức tam giác:
Cộng về với vế ta được:
Mặt khác ta có đường đi trên là đường đi ngắn nhất nên
Theo đó:
Dấu bằng phải xảy ra, dẫn đến dấu bằng của bất đẳng thức tam giác phải xảy ra:
Theo đó, đường đi trên phải nằm trong .
Tính chất số 4 chính là chìa khóa giúp ta giải quyết được *Bài toán đếm số đường đi ngắn nhất_.
¶ Cài đặt
Shortest Path DAG có ý nghĩa về mặt đưa ra nhận xét, các tính chất hơn thay vì được coi như một cấu trúc dữ liệu.
Vì vậy, thông thường mình sẽ không dựng lại cả một đồ thị mới mà sẽ tận dụng lại tài nguyên (Danh sách đỉnh, danh sách cạnh,...) của đồ thị cũ. Chỉ cần chú ý khi duyệt đồ thị, ta cần kiểm tra tính tồn tại của cung dựa trên điều kiện của DAG.
¶ Áp dụng
Sử dụng các tính chất trên, ta có thể giải quyết một số bài toán về đường đi ngắn nhất; sẽ khá khó để có thể giải quyết các bài toán sau đây với những công cụ cơ bản.
¶ VNUOI 2022: DELETE
Cho một đồ thị vô hướng gồm đỉnh và cạnh với trọng số duonwg; trong đó có cạnh loại 1 và cạnh loại 2. Các cạnh loại 2 chỉ nối giữa đỉnh và một đỉnh khác.
Yêu cầu: Hãy đếm số cách xóa một số cạnh loại 2 (Có thể không xóa cạnh nào) sao cho đường đi ngắn nhất từ đỉnh tới các đỉnh khác là không đổi.
Bài toán có thể xem tại https://oj.vnoi.info/problem/vnuoi22_delete
¶ Nhận xét
Trong bài toán trên, điều kiện của các cạnh loại 2 sẽ giúp ta giải bài toán dễ hơn. Tuy nhiên, nếu không có điều kiện ấy thì bài toán vẫn giải được dựa vào Shortest Path DAG.
Xét Shortest Path DAG của đồ thị, sẽ thay đổi ứng với mỗi thay đổi (thêm/xóa cạnh) trên đồ thị ban đầu; ta có một số nhận xét:
- Nếu một cạnh không tạo ra một cung trong , việc xóa nó không ảnh hưởng đến dường đi ngắn nhất từ tới các đỉnh. Lượng đóng góp của cạnh này là .
- Nếu vẫn tồn tại đường đi từ đỉnh đến đỉnh trên thì độ dài đường đi ngắn nhất từ đến trên đồ thị ban đầu là không đổi. (Tính chất số 1 và Tính chất số 2).
Ta qui việc đếm cách xóa cạnh trên đồ thị ban đầu về đếm số cách xóa cung trên .
Mặt khác, do là DAG (Tính chất số 3) Sau khi xóa cung, các đỉnh ban đầu có bậc vào khác 0 thì sau khi xóa cũng phải có bậc vào khác 0.
Ta đếm số cách xóa để các đỉnh có bậc vào khác 0 vẫn tiếp tục khác 0.
¶ Thuật toán
Trước tiên, ta sẽ dựng đồ thị của đồ thị đã cho. Xét đỉnh , gọi:
- là bậc vào của đỉnh
- là số cung "loại 1" vào đỉnh
- là số cung "loại 2" vào đỉnh
Lượng đóng góp của đỉnh , tức là số cách xóa cung vào để bậc của nó tiếp tục bằng 0 hoặc tiếp tục khác 0 là:
- nếu
- nếu vì
- nếu vì
Từ đó, đáp án là tích lượng đóng góp của các đỉnh và các cạnh loại 2 sinh ra cung trong .
Code mẫu:
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
using ll = long long;
constexpr int N = 2e5 + 5;
constexpr int M = 5e5;
constexpr ll mod = 998244353;
constexpr ll Inf = 1e17;
struct Edge {
int u, v, w;
}
s1[M], s2[N];
int n, k, m;
int deg_1[N], deg_2[N];
ll d[N];
// adj[i] = đỉnh kề thông qua các cạnh loại 1
// nadj[i] = đỉnh kề thông qua các cạnh loại 2
vector < pair < int, int >> adj[N], nadj[N];
// Nhập dữ liệu
void Read() {
cin >> n >> m >> k;
for (int i = 1; i <= m; ++i) {
cin >> s1[i].u >> s1[i].v >> s1[i].w;
adj[s1[i].u].emplace_back(s1[i].v, i);
adj[s1[i].v].emplace_back(s1[i].u, i);
}
for (int i = 1; i <= k; ++i) {
s2[i].u = 1;
cin >> s2[i].v >> s2[i].w;
nadj[s2[i].u].emplace_back(s2[i].v, i);
nadj[s2[i].v].emplace_back(s2[i].u, i);
}
}
// Tính a ^ b % mod
ll Pow(ll a, ll b) {
ll ans(1);
for (; b; b >>= 1) {
if (b & 1)
ans = ans * a % mod;
a = a * a % mod;
}
return ans;
}
// Thuật toán tìm đường đi ngắn nhất
// Kết quả trả về mảng d[], d[i] = đường đi ngắn nhất từ x đến i
void ShortestPath(int x) {
// Bạn đọc vui lòng tự cài đặt lại thuật toán
}
// Thực hiện thuật toán
void Solve() {
ll ans(1);
ShortestPath(1);
/* Dựng Shortest Path DAG */
for (int i = 1; i <= m; ++i)
if (d[s1[i].u] + s1[i].w == d[s1[i].v])
++deg_1[s1[i].v];
else if (d[s1[i].v] + s1[i].w == d[s1[i].u])
++deg_1[s1[i].u] = 1;
for (int i = 1; i <= k; ++i)
if (d[s2[i].u] + s2[i].w == d[s2[i].v])
++deg_2[s2[i].v];
else if (d[s2[i].v] + s2[i].w == d[s2[i].u])
++deg_2[s2[i].u];
else
ans = ans * 2 % mod; // Cạnh này không sinh cung
/* Kết thúc dựng Shortest Path DAG */
for (int i = 2; i <= n; ++i)
if (deg_1[i] > 0)
ans = ans * Pow(2, deg_2[i]) % mod;
else if (deg_2[i] > 0)
ans = ans * (Pow(2, deg_2[i]) - 1) % mod;
cout << (ans + mod) % mod;
}
int32_t main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
Read();
Solve();
}
Nhìn đoạn code trên, ta có thể dễ thấy độ phức tạp thời gian của thuật toán là . Thuật toán chạy nhanh hay chậm phụ thuộc phần nhiều vào cách cài đặt hàm ShortestPath.
¶ BIẾN ĐỘNG
Cho một đồ thị vô hướng liên thông gồm đỉnh và cạnh có trọng số dương. Gọi là độ dài đường đi ngắn nhất giữa và .
Yêu cầu: Với mỗi cạnh, hãy đếm số cặp đỉnh mà tăng nếu ta xóa bỏ cạnh này.
Bài toán có thể xem tại https://vjudge.net/problem/Gym-406204L
¶ Nhận xét
Bài toán yêu cầu với mỗi cạnh, đếm số cặp đỉnh mà tăng lên khi xóa cạnh đó. Vậy cạnh này có điều kiện gì mà ảnh hưởng được đến đường đi ngắn nhất từ đến một đỉnh khác? Rõ ràng cạnh này phải thuộc một đường đi ngắn nhất xuất phát từ đỉnh !
Ta dựng ra Shortest Path DAG ; gọi là số đường đỉ từ đỉnh đến đỉnh .
Nếu xóa cung làm tăng thì mọi đường đi từ đến phải thông qua cung này, tức là:
Từ nhận xét ở bài DELETE ta có thể xóa bỏ các cung sao cho mỗi đỉnh trên có bậc tối đa là 1 và đường đi ngắn nhất từ đến các đỉnh là không đổi.
Các "ứng cử viên" là các cung được giữ lại. Có thể chứng minh số cung của khi ấy không quá .
¶ Thuật toán
Ta dựng ra các Shortest Path DAG . Trên :
- Ta duyệt qua các "ứng cử viên" mà trong phần nhận xét đã nói
- Với mỗi ứng cử viên, ta lại duyệt các đỉnh nhằm đếm số lượng đường đi bị tăng nếu xóa "ứng cử viên" đó (Dựa vào điều kiện )
Chú ý:
- Theo tính chất 4, chính là số đường đi ngắn nhất từ đến trên đồ thị ban đầu Ta có thể tính trước đường đi ngắn nhất giữa mọi cặp đỉnh bằng cách thực hiện lần thuật toán Dijkstra cổ điển (Thuật toán Dijkstra với độ phức tạp )
- có thể rất lớn, nên bạn hãy lưu số này trong modulo một số nào đó (Hoặc có thể trong hai modulo); khi so sánh ta sử dụng đồng dư thay vì bằng nhau hoàn toàn.
Vì số lượng ứng cử viên của mỗi DAG là nên độ phức tạp thời gian khi ấy là là chi phí dựng DAG và chi phí duyệt.
Code mẫu:
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
using ll = long long;
constexpr int N = 5e2 + 5;
constexpr ll Inf = 1e17;
// Mình tính cnt(i,j) trong hai modulo nguyên tố là 1e9+7 và 998244353
constexpr int mod[2] = {
1000000007,
998244353
};
inline void Add(int & x,
const int & y,
const int & mod) { // Chỉ là template cộng mod mà thôi
x += y;
if (x >= mod)
x -= mod;
}
int n, m;
struct Edge {
int u, v, w;
}
e[N * N];
int ans[N * N];
vector < pair < int, int >> adj[N];
vector < int > candidate;
ll d[N][N];
int cnt[N][N][2];
int mark, check[N];
// Thuật toán Dijkstra cổ điển
void Dijkstra(int x, ll d[N]) {
++mark;
fill_n(d, N, Inf);
d[x] = 0;
cnt[x][x][0] = cnt[x][x][1] = 1;
for (int i = 1; i <= n; ++i) {
pair < ll, int > ans = {
Inf,
0
};
for (int j = 1; j <= n; ++j) // Thay vì dùng Hàng đợi ưu tiên, ta duyệt lại toàn bộ
if (check[j] != mark && d[j] < ans.first)
ans = {
d[j],
j
};
if (ans.first == Inf)
break;
check[ans.second] = mark;
for (auto i: adj[ans.second])
if (d[i.first] > ans.first + e[i.second].w) {
d[i.first] = ans.first + e[i.second].w;
cnt[x][i.first][0] = cnt[x][ans.second][0];
cnt[x][i.first][1] = cnt[x][ans.second][1];
}
else if (d[i.first] == ans.first + e[i.second].w) {
Add(cnt[x][i.first][0], cnt[x][ans.second][0], mod[0]);
Add(cnt[x][i.first][1], cnt[x][ans.second][1], mod[1]);
}
}
}
// dfs để tìm tập "ứng cử viên"
void dfs(int v, int p, ll d[N]) {
for (auto i: adj[v])
if (i.first != p && d[i.first] == d[v] + e[i.second].w) {
candidate.emplace_back(i.second);
dfs(i.first, v, d);
}
}
int32_t main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
cin >> e[i].u >> e[i].v >> e[i].w;
adj[e[i].u].emplace_back(e[i].v, i);
adj[e[i].v].emplace_back(e[i].u, i);
}
// Thực hiện n lần Dijkstra và cho chạy thuật toán đếm đường đi ngắn nhất song song với Dijkstra
for (int i = 1; i <= n; ++i)
Dijkstra(i, d[i]);
for (int i = 1; i <= n; ++i) {
candidate.clear();
dfs(i, -1, d[i]);
for (auto j: candidate) {
// Xác định chiều của cung
int v = d[i][e[j].u] > d[i][e[j].v] ? e[j].u : e[j].v;
int u = e[j].u + e[j].v - v;
for (int t = 1; t <= n; ++t)
if (d[i][u] + e[j].w + d[v][t] == d[i][t] && 1 ll * cnt[i][u][0] * cnt[v][t][0] % mod[0] == cnt[i][t][0] && 1 ll * cnt[i][u][1] * cnt[v][t][1] % mod[1] == cnt[i][t][1])
++ans[j];
}
}
for (int i = 1; i <= m; ++i)
cout << ans[i] / 2 << "\n"; // Vì mỗi cặp định được tính hai lần nên kết quả phải chia cho 2
}