¶ Li-chao Tree (Cây phân đoạn trên tập đường thẳng)
Tác giả:
- Nguyễn Tấn Minh - THPT Chuyên Lê Hồng Phong, TPHCM.
Reviewer:
- Đoàn Gia Huy - HUS High School for Gifted Students
- Nguyễn Quang Minh - HUS High School for Gifted Students
¶ Giới thiệu
Li-chao tree (cây phân đoạn trên tập đường thẳng) là một biến thể của Segment tree[1] (cây phân đoạn) cho phép quản lý một tập đường thẳng với thao tác sau:
- Thêm một hàm vào tập đường thẳng.
- Cho một số nguyên (với ), gọi là tập đường thẳng hiện tại, tính hoặc .
Cả hai thao tác trên đều có thể được xử lý trong .
Tổng quát hơn, Li-chao tree có thể xử lý những loại hàm có tính chất sau:
Gọi và là hai hàm bất kì thuộc loại này sao cho và xác định trên khoảng đang xét. Hai hàm này cần thỏa một trong hai tính chất:
- Nếu thì với và .
- Nếu thì với và .
Hoặc ta cũng có thể biến đổi điều kiện này thành cắt tại tối đa điểm.
Trong bài viết này, ta chỉ quan tâm đến phương trình đường thẳng, loại phương trình thỏa tính chất nêu trên:
Ngoài ra, ta giả sử thao tác loại sẽ thực hiện tìm , thao tác tìm được thực hiện tương tự.
¶ Ý tưởng
¶ Đường thẳng và tính chất của phương trình đường thẳng
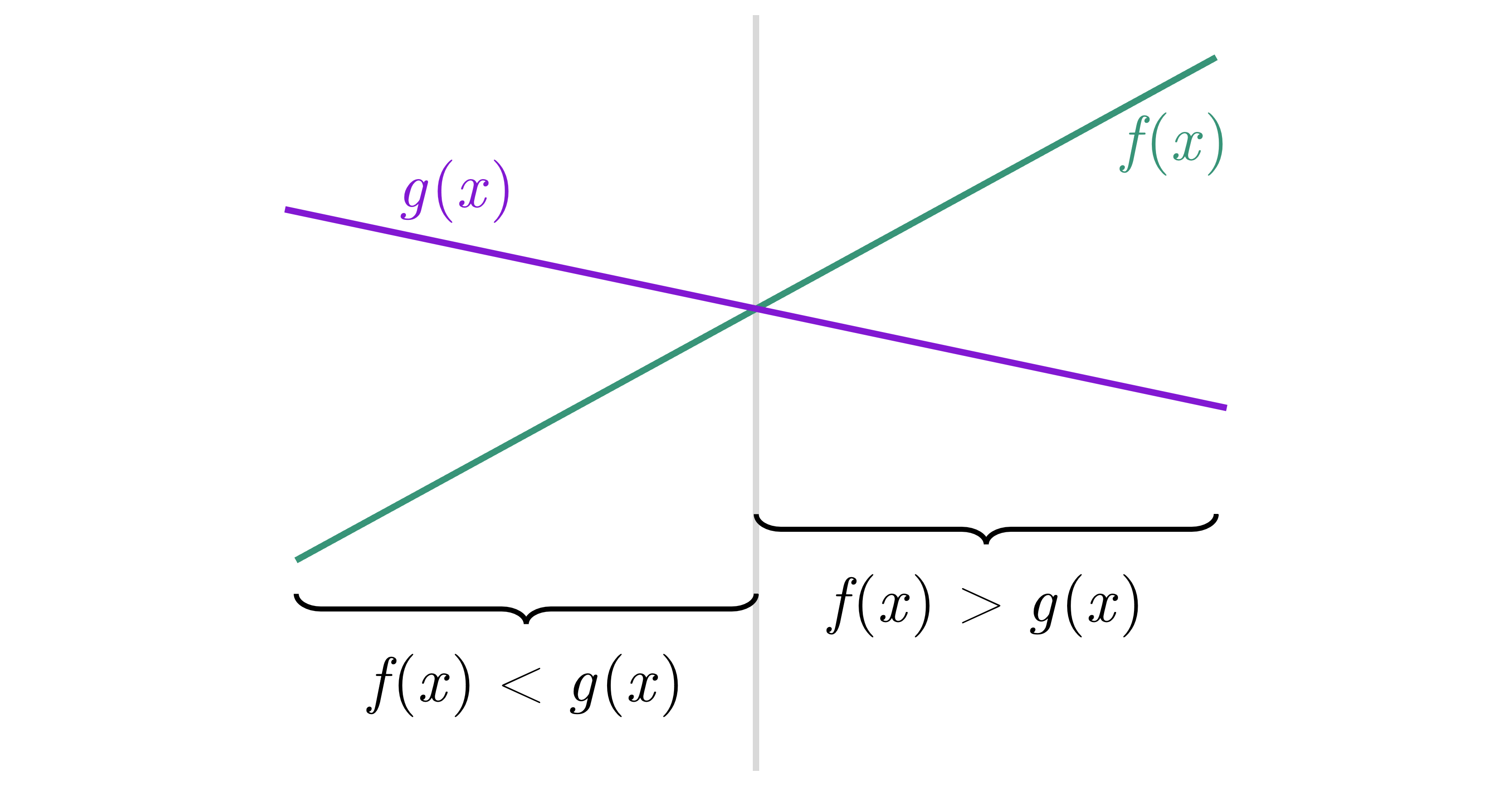
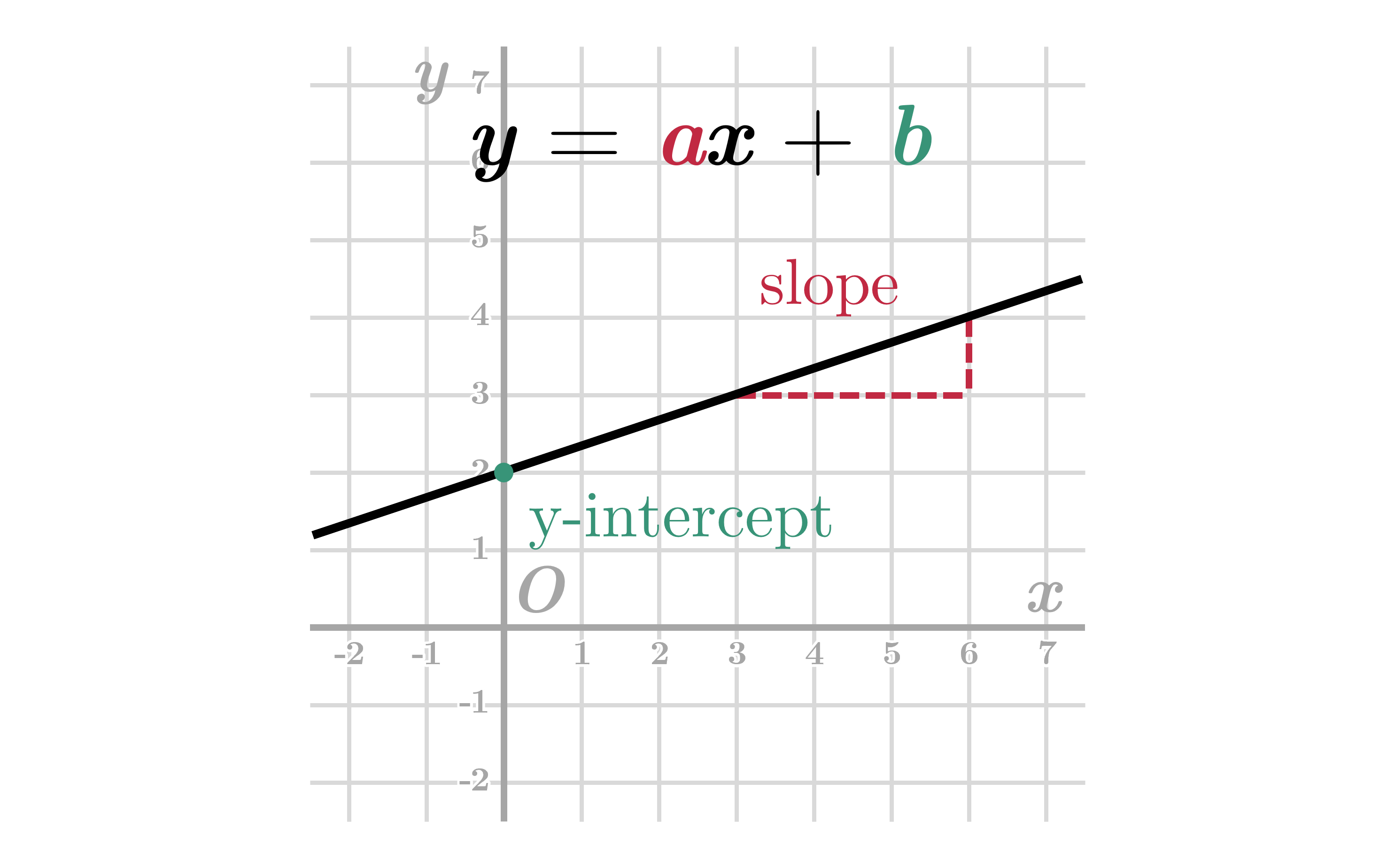
Trong toán học, ta đã biết một đường thẳng có thể biểu diễn dưới dạng một phương trình tuyến tính bậc có dạng . Trong đó:
- Hệ số góc hay độ dốc (slope) thể hiện mức độ tăng/giảm nhanh/chậm của hàm. Ví dụ, hàm tăng nhanh hơn hàm do có hệ số dốc lớn hơn. Tương tự, hàm giảm nhanh hơn hàm do có hệ số góc bé hơn.
- Hệ số tự do (y-intercept) cho biết phương trình cắt trục tại điểm .
¶ Tính chất của tập đường thẳng
Nếu vẽ một tập đường thẳng bất kì ra, ta thấy những đoạn đóng góp vào đáp án, tạm gọi là "min-line", sẽ tạo thành nửa trên của một bao lồi[2] (upper hull) như sau:
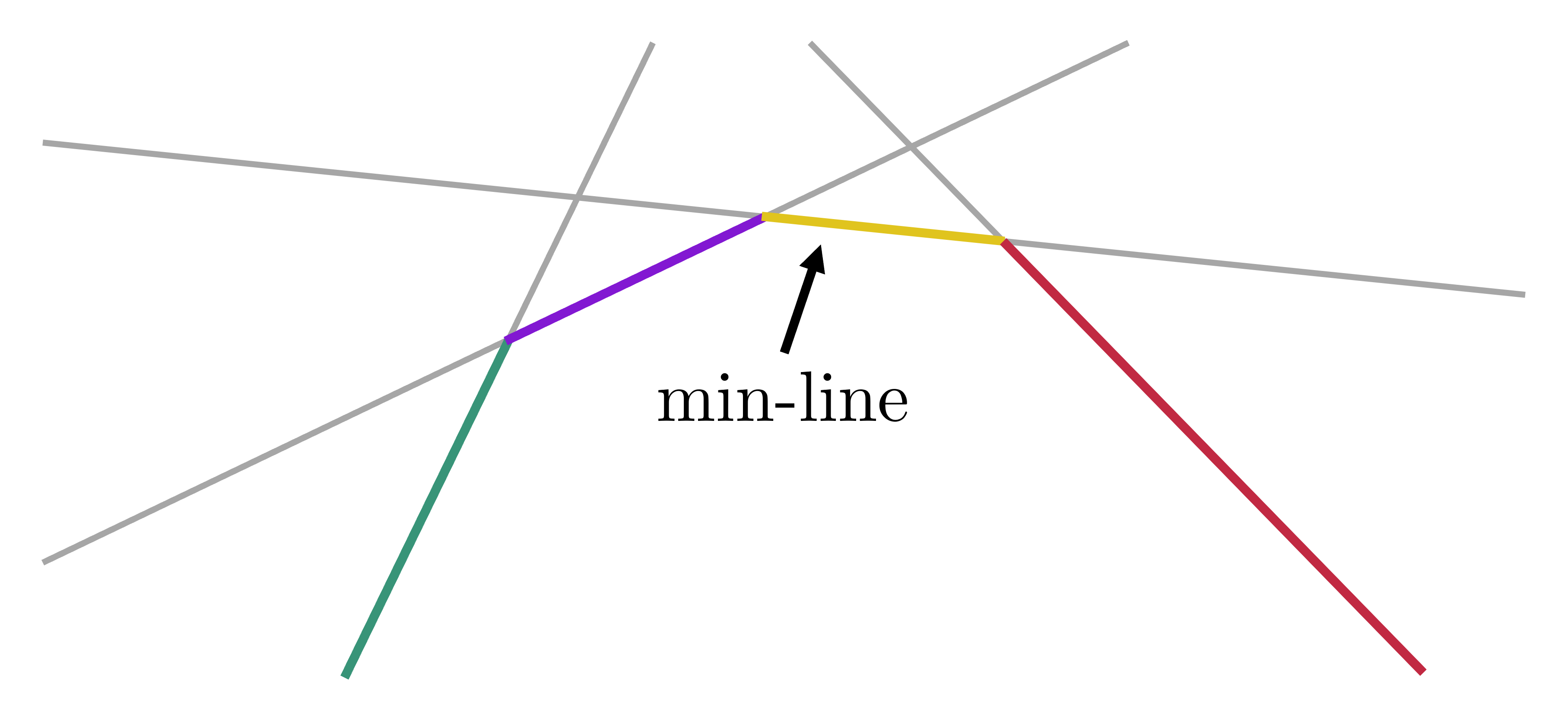
Mỗi đường thẳng đóng góp vào min-line duy nhất một đoạn liên tiếp và từ trái qua phải, thứ tự xuất hiện của các đường thẳng là thứ tự giảm dần theo hệ số góc của chúng. Một số đường thẳng có thể không đóng góp gì vào min-line.
Đối với max-line thì sao?
Max-line sẽ tạo thành nửa dưới của một bao lồi (lower hull), với các đường thẳng đóng góp vào max-line từ trái qua phải là thứ tự tăng dần theo hệ số góc.
¶ Xây dựng mảng
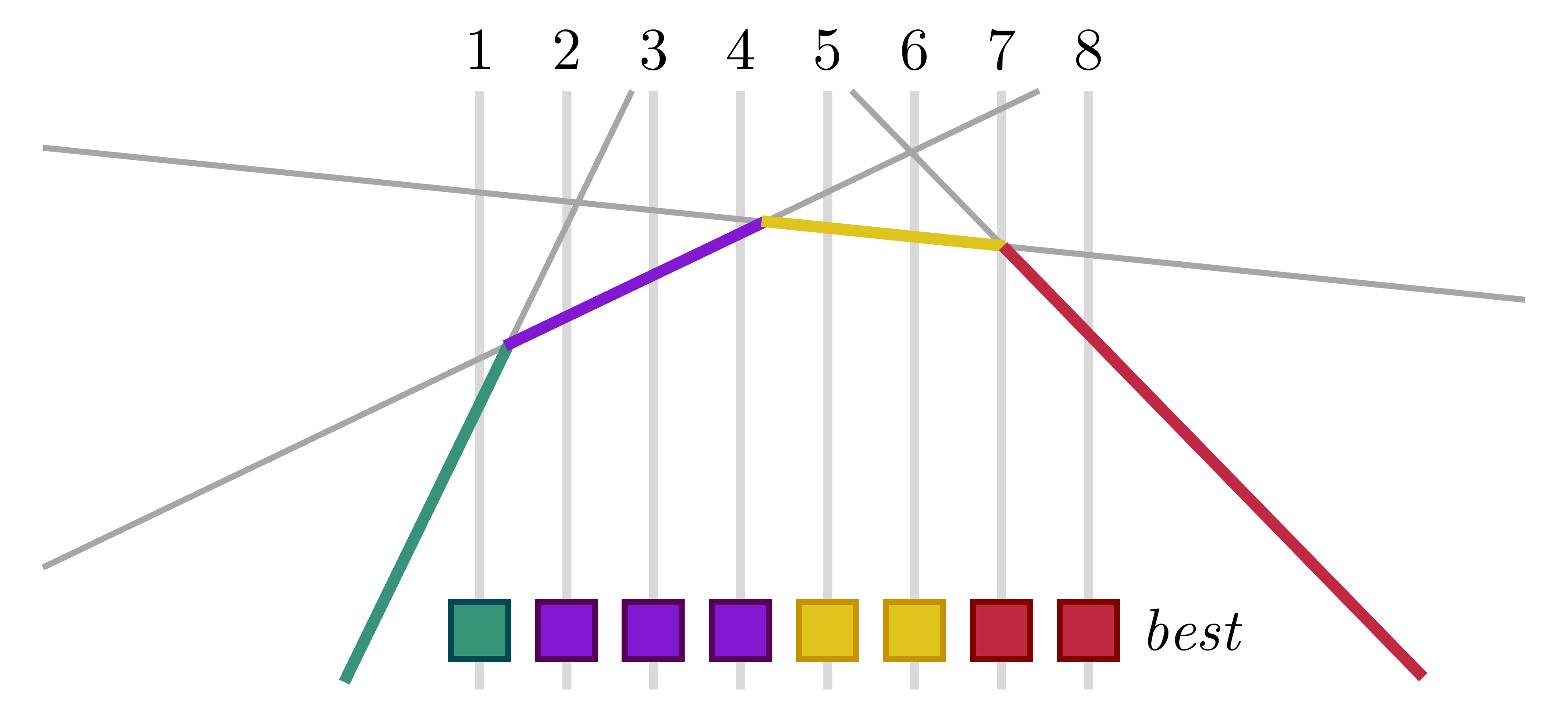
Giả sử ta có mảng gồm phần tử với là đường thẳng đóng góp vào min-line tại . Với nhận xét được nêu trên, khi thêm một đường thẳng vào tập, có thể thấy một số giá trị liên tiếp sẽ được gán cho đường thẳng mới.
Ví dụ, sau đây là ảnh minh họa cho mảng quản lý một upper hull tại các vị trí .
Lưu ý
Chúng ta phải lưu cả phương trình đường thẳng thay vì chỉ đơn giản là giá trị của hàm tại điểm đó. Nếu chỉ lưu giá trị của hàm tại điểm , thao tác cập nhật sẽ không còn đơn giản là gán một đoạn cho cùng một phương trình đường thẳng, mà là gán giá trị theo bậc thang.
Đến đây, ta có thể liên tưởng đến Segment tree để xử lý cập nhật đoạn (range update) và truy cập điểm (point access), sử dụng lazy propagation. Tuy nhiên, đối với Li-chao tree, ta sẽ phải làm khác đi một chút so với Segment tree truyền thống.
¶ Ôn lại Segment tree
Trước khi đi đến ý tưởng của Li-chao, ta sẽ tìm hiểu cách sử dụng Segment tree để xử lý bài toán sau. Cho mảng gồm phần tử và truy vấn thuộc một trong hai loại:
- Cho ba số nguyên , gán đối với mọi thỏa .
- Cho số nguyên , tính .
Đối với dạng bài toán này, chúng ta có thể xây dựng Segment tree chỉ có mảng lazy và không cần bước push-down như sau:
- Đối với truy vấn loại , tách đoạn thành đoạn (theo ý tưởng Segment tree truyền thống) và cập nhật những nút tương ứng.
- Đối với truy vấn loại , lấy của các nút quản lý vị trí , tức là đường đi từ gốc xuống nút lá tương ứng.
Code tham khảo
void update (int a, int b, int x, int k, int l, int r) {
/*
a..b: khoảng cần cập nhật
x: giá trị cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
if (b < l || r < a) return;
if (a <= l && r <= b) {
lazy[k] = min(lazy[k], x);
return;
}
int mid = (l + r) >> 1;
update(a, b, x, 2 * k, l, mid);
update(a, b, x, 2 * k + 1, mid + 1, r);
}
int query (int p, int k, int l, int r) {
/*
p: vị trí được truy vấn
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
int ans = lazy[k], mid = (l + r) >> 1;
if (l == r) return ans;
if (p <= mid)
return min(ans, query(p, 2 * k, l, mid));
else return min(ans, query(p, 2 * k + 1, mid + 1, r));
}
Bây giờ, ta sẽ tìm cách biển đổi cách xử lý trên để áp dụng cho tập đường thẳng.
¶ Thuật toán
¶ Thao tác loại : Thêm đường thẳng
Đầu tiên, đưa đường thẳng mới vào nút gốc của Li-chao tree. Tại mỗi nút , gọi:
- là hàm được đưa vào.
- là hàm mà nút đang chứa.
- là đoạn mà nút quản lý, .
- là đoạn mà hàm sẽ đóng góp vào min-line (ta chưa biết đoạn này là gì).
Ta thực hiện chia để trị[3] với trường hợp chính như sau:
¶ Trường hợp 1
Khi đó, đoạn chỉ nằm ở một trong hai khoảng hoặc . Đồng nghĩa với việc hàm không thay đổi và hàm sẽ được đưa xuống cây con. Để chọn cây con cho hàm , ta cần so sánh hệ số góc của so với , cụ thể:
- Nếu hệ số góc của lớn hơn , hàm sẽ được đưa xuống cây con bên trái và chia để trị tiếp cho đoạn tương ứng là .
- Nếu hệ số góc của bé hơn , hàm sẽ được đưa xuống cây con bên phải và chia để trị tiếp cho đoạn tương ứng là .
- Nếu hệ số góc của và bằng nhau, khi đó đường thẳng nằm song song và ở phía trên nên chắc chắn sẽ không đóng góp gì vào min-line. Ta có thể không làm gì cả hoặc gộp trường hợp này vào một trong hai trường hợp nêu trên.
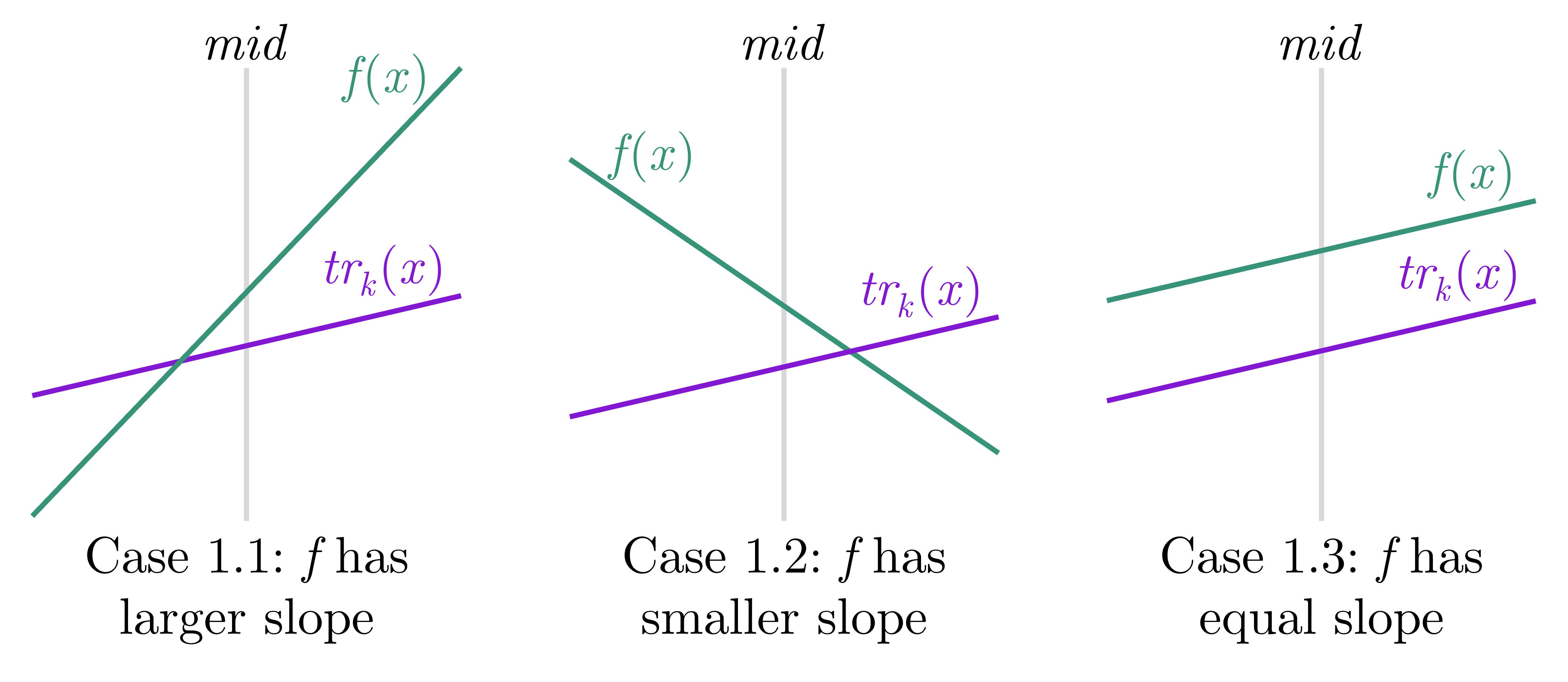
¶ Trường hợp 2
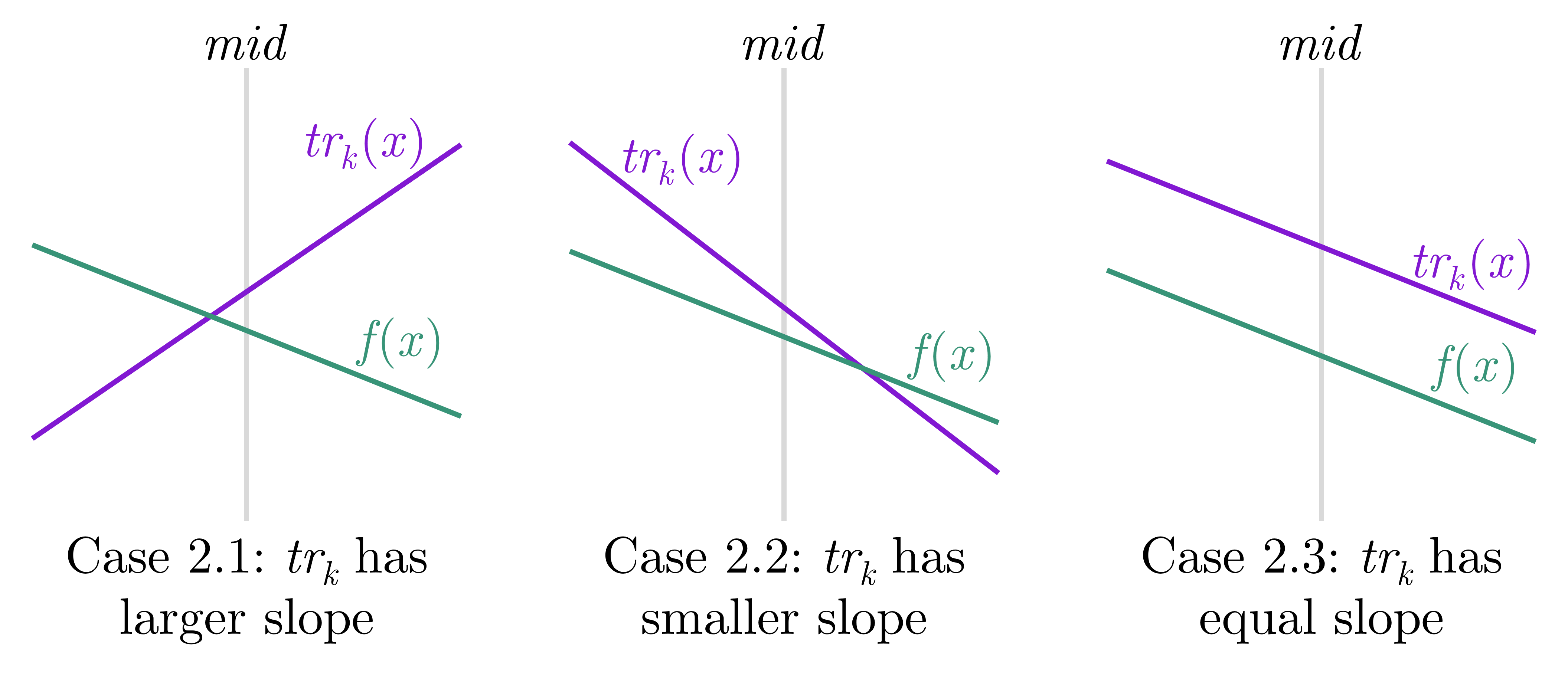
Khi đó, đoạn nằm ở cả hai khoảng và . Đồng nghĩa với việc hàm sẽ bị thay thế bởi hàm . Ta gán bằng , thao tác này tương đương với gán cho đoạn
Lưu ý
Tuy phép gán cho cả đoạn có thể sẽ thừa so với đoạn nhưng ta đang thao tác với hàm / nên điều này không làm ảnh hưởng kết quả.
Đường thẳng ban đầu vẫn còn có thể đóng góp vào min-line ở một trong hai khoảng hoặc . Do đó, ta đưa đường thẳng này xuống một trong hai cây con. Việc chọn cây con tương tự trường hợp 1 nhưng bây giờ hàm và đổi vai trò cho nhau.
¶ Xử lý tổng quát
Trên thực tế, ta có thể giảm số trường hợp cần xử lý bằng một trong hai cách:
- Quy ước .
- Quy ước hệ số góc của lớn hơn hoặc bằng .
Nếu điều kiện quy ước không được thỏa, ta chỉ việc tráo đổi hai đường thẳng cho nhau. Trong bài viết này, mình sẽ sử dụng cách làm đầu tiên.
Ngoài ra, để tránh phải xử lý nửa khoảng khi chia để trị, nếu ta chỉ quan tâm các vị trí là số nguyên, ta sẽ chia khoảng thành và thay vì và như trên, với .
Tương tự, nếu ta quan tâm cả những vị trí là số thực, ta có thể chia đoạn thành và với và là hằng số nhỏ khoảng đến lần sai số tổi thiểu (thường là hoặc ).
Như vậy, ta có thể hiểu rằng là đường thẳng tối ưu cho vị trí , nếu chưa tính các đường thẳng được lưu tại các nút tổ tiên của .
¶ Trường hợp cơ sở (base case)
Quá trình chia để trị sẽ kết thúc khi ta đi xuống đến nút lá, khi đó, ta chỉ việc so sánh hai hàm và xem hàm nào tốt hơn cho vị trí tương ứng rồi gán cho hàm tối ưu.
¶ Thao tác loại : Tìm hàm tối ưu cho điểm
Tương tự với Segment tree, để lấy dữ liệu cho vị trí , ta kết hợp dữ liệu ở các nút quản lý . Nói cách khác, ta sẽ thực hiện di chuyển từ gốc của Li-chao tree xuống nút lá tương ứng với vị trí và lấy đường thẳng tối ưu nhất trên đường đi.
¶ Cài đặt
¶ Li-chao tree cho tập đường thẳng
Để thuận tiện cho việc cài đặt, ta cần tạo ra một struct biểu diễn đường thẳng.
struct line {
ll a, b;
line() : a(0), b(0) {}
line (ll a, ll b) : a(a), b(b) {}
ll calc (ll x) { return a * x + b; }
ll slope() { return a; }
};
Ban đầu, tất cả các nút của Li-chao tree chứa đường thẳng (tức là đường thẳng song song với trục nằm rất cao). Ở đây mình chọn vô cực là LLONG_MAX.
struct liChao {
vector<line> tr;
liChao() {}
liChao (int sz) : tr(4 * sz, line(0, LLONG_MAX)) {}
void update (line f, int k, int l, int r) {
/*
f: đường thẳng cần cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
if (l == r) {
tr[k] = (f.calc(l) < tr[k].calc(l) ? f : tr[k]);
return;
}
int mid = (l + r) >> 1;
// để giảm số trường hợp cần xử lý, giả sử tr[k] tốt hơn f cho vị trí mid
if (f.calc(mid) < tr[k].calc(mid)) swap(tr[k], f);
// trường hợp 1.1, đường thẳng f được đưa xuống cây con trái
if (f.slope() > tr[k].slope())
update(f, 2 * k, l, mid);
// trường hợp 1.2, đường thẳng f được đưa xuống cây con phải
if (f.slope() < tr[k].slope())
update(f, 2 * k + 1, mid + 1, r);
}
ll query (int pos, int k, int l, int r) {
/*
pos: vị trí được truy vấn
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
ll cur = tr[k].calc(pos);
int mid = (l + r) >> 1;
// thực hiện di chuyển từ nút gốc xuống nút lá tương ứng, tương tự như Segment tree
if (l == r) return cur;
if (pos <= mid)
return min(cur, query(pos, 2 * k, l, mid));
else return min(cur, query(pos, 2 * k + 1, mid + 1, r));
}
};
Đánh giá độ phức tạp:
- Thời gian: cho mỗi thao tác.
- Bộ nhớ: cho cả Li-chao tree.
¶ Li-chao tree tổng quát
Khi cài đặt Li-chao tree cho các hàm không phải phương trình đường thẳng, ta không thể chọn cây con để đưa hàm xuống bằng cách so sánh hệ số góc nữa. Lúc này, ta sử dụng điều kiện tổng quát:
- Nếu thì hàm sẽ được đưa xuống cây con trái.
- Nếu thì hàm sẽ được đưa xuống cây con phải.
void update (line f, int k, int l, int r) {
if (l == r) {
tr[k] = (f.calc(l) < tr[k].calc(l) ? f : tr[k]);
return;
}
int mid = (l + r) >> 1;
if (f.calc(mid) < tr[k].calc(mid)) swap(tr[k], f);
if (f.calc(l) < tr[k].calc(l))
update(f, 2 * k, l, mid);
if (f.calc(r) < tr[k].calc(r))
update(f, 2 * k + 1, mid + 1, r);
}
Các hàm còn lại vẫn sẽ được cài đặt như cũ. Lưu ý rằng, khi cài đặt như thế này, chúng ta cần để ý để hằng số cho việc tính toán các hàm, vì chúng được gọi khá nhiều.
¶ Mở rộng: Các tối ưu và biến thể Li-chao tree
¶ Tối ưu bộ nhớ
Đối với Li-chao tree kinh điển, ta có thể tối ưu bộ nhớ một chút bằng cách định nghĩa lại cách chia để trị. Cụ thể, với một nút quản lý đoạn :
- Nút con bên trái quản lý đoạn .
- Nút con bên phải quản lý đoạn .
Với cách làm này, không khó để chứng minh rằng ta chỉ cần đúng nút cho Li-chao tree và việc đánh số cũng trở nên dễ dàng hơn khi ta có thể dùng là chỉ số cho các nút.
Code tham khảo
struct liChao {
vector<line> tr;
liChao() {}
liChao (int sz) : tr(sz + 1, line(0, LLONG_MAX)) {}
void update (line f, int l, int r) {
/*
f: đường thẳng cần cập nhật
mid: nút hiện tại
l..r: khoảng mà nút quản lý
*/
if (l > r) return;
int mid = (l + r) >> 1;
if (l == r) {
tr[mid] = (f.calc(l) < tr[mid].calc(l) ? f : tr[mid]);
return;
}
// việc cập nhật được thực hiện tương tự Li-chao tree cơ bản
if (f.calc(mid) < tr[mid].calc(mid)) swap(tr[mid], f);
if (f.slope() > tr[mid].slope())
update(f, l, mid - 1); // trường hợp 1.1
if (f.slope() < tr[mid].slope())
update(f, mid + 1, r); // trường hợp 1.2
}
ll query (int p, int l, int r) {
/*
p: vị trí được truy vấn
mid: nút hiện tại
l..r: khoảng mà nút quản lý
*/
int mid = (l + r) >> 1;
ll cur = tr[mid].calc(p);
if (p == mid) return cur;
if (p < mid) return min(query(p, l, mid - 1), cur);
if (p > mid) return min(query(p, mid + 1, r), cur);
}
};
Lưu ý, với cách cài đặt này, một base case mới sẽ phát sinh đó là hàm update sẽ được gọi với . Ví dụ, khi được gọi với đoạn , hàm sẽ chia thành đoạn và .
Hiệu quả của tối ưu có thể được thể hiện qua bài Building Bridges (CEOI 2017)[4] như sau:
| Solution | Thời gian chạy | Bộ nhớ |
|---|---|---|
| Chưa tối ưu | 70 mili giây | 66540 kB |
| Đã tối ưu | 56 mili giây | 19564 kB |
Các bạn có thể tham khảo code của mình tại đây.
¶ Li-chao tree cho tập đoạn thẳng
Ta có thể biến đổi Li-chao tree để xử lý tập đoạn thẳng với thao tác như sau:
- Cho bốn số nguyên , thêm đoạn thẳng với vào tập đoạn thẳng.
- Cho một số nguyên (với ), gọi là tập đường thẳng hiện tại, tính .
Bài toán này khác bài toán gốc ở chỗ, thay vì phải xử lý đường thẳng, ta phải xử lý đoạn thẳng, tức là:
Tập đoạn thẳng bấy giờ không còn là nửa trên của bao lồi nữa. Tuy nhiên, với truy vấn loại , ta có thể chia đoạn thành đoạn (theo ý tưởng của Segment tree) rồi thực hiện thao tác cập nhật của Li-chao tree bắt đầu từ các nút tương ứng. Tổng độ phức tạp thời gian là .
Lưu ý
Đối với biến thể Li-chao tree này, ta không thể sử dụng tối ưu bộ nhớ.
Truy vấn loại được xử lý bình thường trong .
Code tham khảo
struct liChao {
vector<line> tr;
liChao() {}
liChao (int sz) : tr(4 * sz, line(0, LLONG_MAX)) {}
void addLine (line f, int k, int l, int r) {
/*
f: đường thẳng cần cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
if (l == r) {
tr[k] = (f.calc(l) < tr[k].calc(l) ? f : tr[k]);
return;
}
int mid = (l + r) >> 1;
if (f.calc(mid) < tr[k].calc(mid)) swap(tr[k], f);
if (f.slope() > tr[k].slope())
addLine(f, 2 * k, l, mid); // trường hợp 1.1
if (f.slope() < tr[k].slope())
addLine(f, 2 * k + 1, mid + 1, r); // trường hợp 1.2
}
void update (int a, int b, line f, int k, int l, int r) {
/*
a..b: khoảng cần cập nhật
f: đường thẳng cần nhập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
if (b < l || r < a) return;
// thực hiện thao tác cập nhật của Li-chao tree cơ bản
// khi khoảng mà nút quản lý nằm gọn trong khoảng cần cập nhật
if (a <= l && r <= b) return addLine(f, k, l, r), void();
// chia để trị tương tự Segment tree
int mid = (l + r) >> 1;
update(a, b, f, 2 * k, l, mid);
update(a, b, f, 2 * k + 1, mid + 1, r);
}
ll query (int pos, int k, int l, int r) {
/*
pos: vị trí được truy vấn
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
ll cur = tr[k].calc(pos);
int mid = (l + r) >> 1;
if (l == r) return cur;
if (pos <= mid)
return min(cur, query(pos, 2 * k, l, mid));
else return min(cur, query(pos, 2 * k + 1, mid + 1, r));
}
};
¶ Li-chao tree trên mảng thưa (Sparse Li-chao tree)
Tương tự Sparse Segment tree[5], chúng ta cũng có thể sử dụng Li-chao tree trên mảng thưa sử dụng con trỏ. Cụ thể, khi quá lớn (ví dụ: ), việc sử dụng bộ nhớ là không thể. Khi đó, ta chỉ tạo các nút cho Li-chao mỗi khi cần cập nhật một nút chưa được tạo.
Có thể thấy, mỗi thao tác cập nhật sẽ thêm vào nút mới. Do đó, độ phức tạp bộ nhớ của Sparse Li-chao tree sau thao tác cập nhật là .
Thao tác truy vấn / thực hiện như bình thường, cần lưu ý tránh truy cập vào con trỏ nullptr.
Code tham khảo
const int M = 1e9;
struct node {
line tr;
node *lpt, *rpt;
node() : tr(0, LLONG_MAX), lpt(nullptr), rpt(nullptr) {}
int divi (int a, int b) { // phép chia làm tròn xuống
return a / b - ((a ^ b) < 0 && a % b);
}
void update (line f, int l = -M, int r = M) {
/*
f: đường thẳng cần cập nhật
l..r: khoảng mà nút quản lý
*/
if (l == r) {
tr = (f.calc(l) < tr.calc(l) ? f : tr);
return;
}
int mid = divi(l + r, 2);
if (f.calc(mid) < tr.calc(mid)) swap(tr, f);
if (f.slope() > tr.slope()) {
if (lpt == nullptr) lpt = new node(); // khởi tạo bộ nhớ cho cây con trái
lpt->update(f, l, mid); // trường hợp 1.1
}
if (f.slope() < tr.slope()) {
if (rpt == nullptr) rpt = new node(); // khởi tạo bộ nhớ cho cây con phải
rpt->update(f, mid + 1, r); // trường hợp 1.2
}
}
ll query (int pos, int l = -M, int r = M) {
/*
pos: vị trí được truy vấn
l..r: khoảng mà nút quản lý
*/
ll cur = tr.calc(pos);
int mid = divi(l + r, 2);
if (l == r) return cur;
// lưu ý: chỉ được di chuyển xuống cây con khi nó được khởi tạo bộ nhớ sẵn
if (pos <= mid)
return min(cur, lpt == nullptr ? LLONG_MAX : lpt->query(pos, l, mid));
else
return min(cur, rpt == nullptr ? LLONG_MAX : rpt->query(pos, mid + 1, r));
}
};
Lưu ý, khi tính cho số âm, ta cần viết lại hàm chia làm tròn xuống.
¶ Tìm hàm tối ưu thứ trên Li-chao tree
Ở những phần trên, chúng ta đã tìm hiểu cách tìm đường thẳng tối ưu nhất cho một vị trí bất kỳ. Với Li-chao tree, ta còn có thể tìm đường thẳng tối ưu thứ . Cụ thể hơn, ta có thể biến đổi Li-chao tree để hỗ trợ hai loại thao tác sau:
- Thêm một hàm vào tập đường thẳng.
- Cho một số nguyên (với ) và (với không quá kích thước tập đường thẳng). Gọi là tập đường thẳng hiện tại, tìm phần tử thứ trong dãy sau khi đã sắp xếp tăng dần.
¶ Ý tưởng
Thoạt đầu, ta sẽ nghĩ đến cách lưu đường thẳng tối ưu nhất ở mỗi nút. Khi số đường thẳng được lưu tại một nút vượt quá , ta sẽ lấy đường thẳng tệ nhất đưa xuống một trong hai cây con.
Tuy nhiên, sẽ có một số trường hợp đường thẳng tệ nhất này còn phải đưa xuống cả hai cây con, ví dụ, với trường hợp sau:
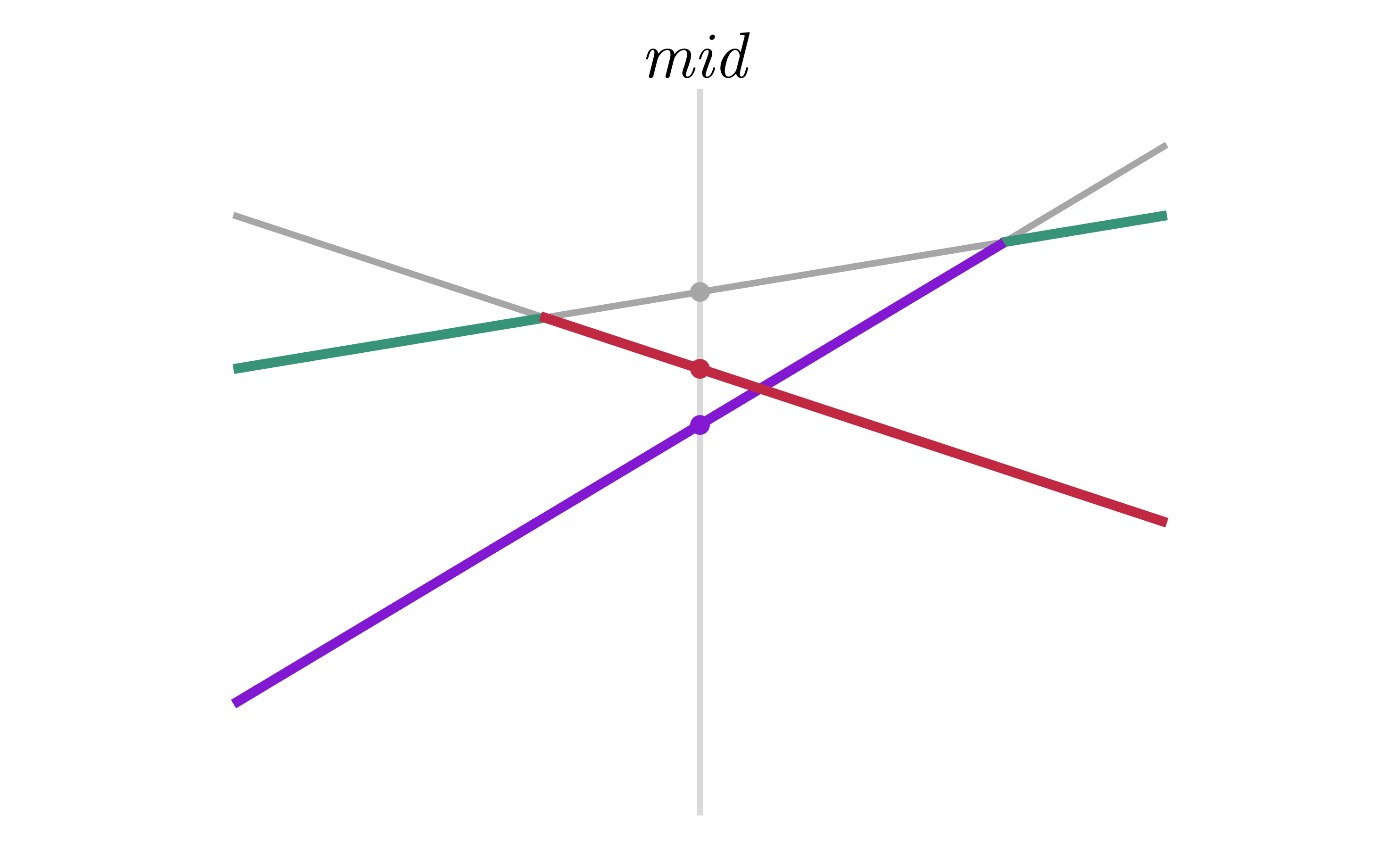
Như vậy, phải lưu bao nhiêu đường thẳng mới đủ?
Ta biết rằng, khi một đường thẳng nằm dưới tại , nó sẽ nằm dưới trong khoảng hoặc .
Xét nút đang bị thừa một đường thẳng, gọi là số đường thẳng nằm dưới đường thẳng tệ nhất trong khoảng , là số đường thẳng nằm dưới đường thẳng tệ nhất trong khoảng . Dễ thấy, để đường thẳng tệ nhất này không được đưa xuống cây con trái thì . Tương tự, để đường thẳng tệ nhất không được đưa xuống cây con phải thì .
Ta muốn đường thẳng tệ nhất này chỉ được đưa xuống tối đa một nút con giống như cơ chế hoạt động của Li-chao tree truyền thống. Do đó, một trong hai giá trị hoặc phải , tức bài toán của chúng ta bây giờ là cực tiểu hóa sao cho .
Không khó để chứng minh câu trả lời là .
¶ Thuật toán
Như vậy, với mỗi nút của Li-chao tree, ta sẽ lưu một danh sách giữ lại đường thẳng tốt nhất (có giá trị bé nhất) được đưa vào. Khi đưa một đường thẳng vào nút, nếu số lượng nút trong danh sách lên đến , ta chọn đường thẳng tệ nhất (có giá trị lớn nhất) rồi đưa xuống một trong hai cây con:
- Trong đường thẳng còn lại, nếu số đường thẳng có hệ số góc lớn hơn đường thẳng tệ nhất là nhỏ hơn , ta đưa đường thẳng tệ nhất xuống cây con trái.
- Trong đường thẳng còn lại, nếu số đường thẳng có hệ số góc bé hơn đường thẳng tệ nhất là nhỏ hơn , ta đưa đường thẳng tệ nhất xuống cây con phải.
Để lấy đường thẳng tối ưu thứ tại vị trí , ta đi từ gốc xuống nút lá tương ứng của vị trí và duy trì một danh sách chứa đường thẳng tốt nhất.
Như vậy, độ phức tạp thời gian cho mỗi thao tác cập nhật và truy vấn là . Độ phức tạp bộ nhớ là với là số đường thẳng được đưa vào.
¶ Cài đặt
Để thuận tiện cho việc cài đặt, mình sử dụng hàm nth_element giúp sắp xếp lại mảng sao cho phần tử ở vị trí thứ sẽ nằm đúng vị trí của nó nếu mảng được sắp xếp, những phần tử còn lại được xếp ngẫu nhiên. Hàm này tốn độ phức tạp gần tuyến tính.
Lưu ý, với cách cài đặt này, danh sách các đường thẳng trong một nút sẽ không được sắp xếp theo thứ tự tối ưu.
Code tham khảo
struct liChao {
vector<vector<line>> tr;
int mkth;
liChao (int sz, int k) : tr(4 * sz), mkth(k) {}
void update (line cur, int k, int l, int r) {
/*
cur: đường thẳng cần cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
tr[k].push_back(cur);
if (tr[k].size() <= 2 * mkth - 1) return;
// chèn đường thẳng mới vào và đưa đường thẳng tệ nhất ra ngoài
int mid = (l + r) >> 1;
nth_element(tr[k].begin(), tr[k].end() - 1, tr[k].end(),
[&] (line a, line b) {return a.calc(mid) < b.calc(mid);}); // đưa đường thẳng tệ nhất ra cuối vector
line worst = tr[k].back();
tr[k].pop_back();
if (l == r) return;
// đếm số đường thẳng được lưu ở nút hiện tại mà tốt hơn đường thẳng tệ nhất
// trong khoảng [l; mid], bằng cách so sánh hệ số góc của chúng
int dominateLeft = 0;
for (line it : tr[k])
dominateLeft += it.slope() > worst.slope();
// đường thẳng tệ nhất được đưa xuống cây con có
// số đường thẳng tốt hơn nó ít hơn "mkth"
if (dominateLeft < mkth) update(worst, 2 * k, l, mid);
else update(worst, 2 * k + 1, mid + 1, r);
}
void push (vector<ll> &cand, ll val, int kth) {
// thêm một giá trị vào vector và giữ lại k giá trị tốt nhất
cand.push_back(val);
if (cand.size() > kth) {
nth_element(cand.begin(), cand.end() - 1, cand.end());
cand.pop_back();
}
}
void walk (vector<ll> &cand, int pos, int kth, int k, int l, int r) {
/*
cand: vector để duy trì k giá trị tốt nhất
pos: vị trí được truy vấn
kth: thứ hạng của đường thẳng cần tìm
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
for (line cur : tr[k]) push(cand, cur.calc(pos), kth);
if (l == r) return;
int mid = (l + r) >> 1;
if (pos <= mid)
walk(cand, pos, kth, 2 * k, l, mid);
else walk(cand, pos, kth, 2 * k + 1, mid + 1, r);
}
ll query (int pos, int kth, int k, int l, int r) {
/*
pos: vị trí được truy vấn
kth: thứ hạng của đường thẳng cần tìm
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
vector<ll> cand;
walk(cand, pos, kth, k, l, r);
nth_element(cand.begin(), cand.end() - 1, cand.end());
return cand.back();
}
};
¶ Lazy propagation trên Li-chao tree (Extended Li-chao tree)
Tương tự với Segment tree, chúng ta hoàn toàn có thể áp dụng Lazy propagation với Li-chao tree, tạo ra những cấu trúc dữ liệu mạnh có thể hỗ trợ những thao tác mà chỉ có Extended Li-chao tree mới làm được.
¶ Bài toán 1
Cho một mảng kích thước và truy vấn online thuộc một trong ba dạng:
- Chèn đoạn thẳng: Cho bốn số nguyên , gán với mọi .
- Tăng đoạn theo dạng bậc thang: Cho bốn số nguyên , tăng lên đơn vị, với mọi .
- Truy vấn điểm: Cho số nguyên , trả về .
Giới hạn:
- .
- .
Với thao tác loại và , chúng ta có thể cài đặt tương tự Li-chao tree quản lý đoạn thẳng như trên. Bây giờ, chúng ta sẽ tìm cách xử lý thao tác loại với Li-chao tree.
¶ Tính chất của phép tăng đoạn theo dạng bậc thang
Ta đã biết, một thao tác tăng theo dạng bậc thang có thể biểu diễn dưới dạng một phương trình đường thẳng, tạm gọi là hàm cập nhật. Hơn nữa, tổng của hai phương trình đường thẳng, cũng là một phương trình đường thẳng. Cụ thể, với hàm và , tổng của chúng là hàm .
Như vậy, ta có thể tưởng tượng một thao tác tăng đoạn theo dạng bậc thang lên một đoạn thẳng chính là "bẻ gãy" đoạn thẳng này tại điểm rồi thay đoạn ở giữa thành tổng của nó và hàm cập nhật.
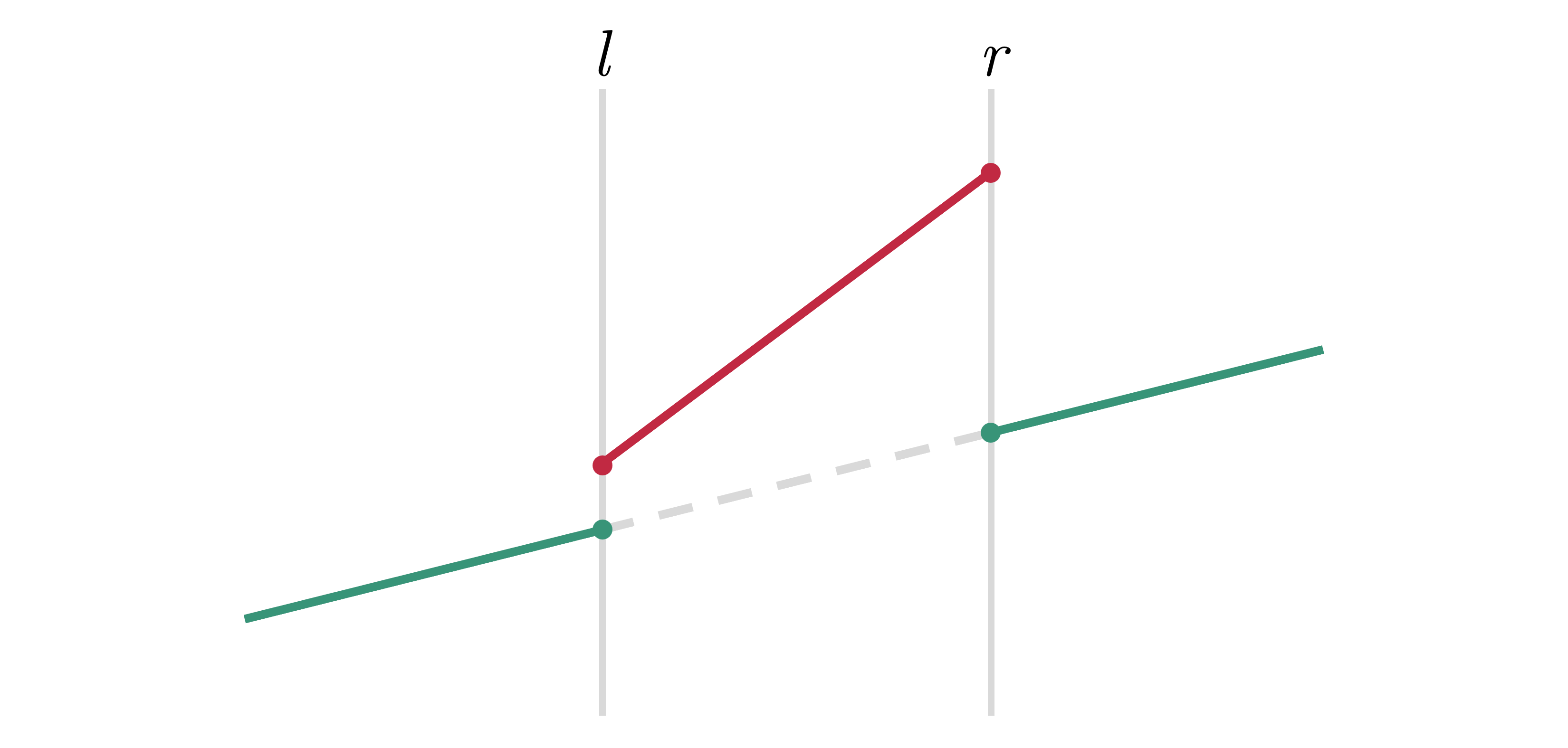
¶ Ý tưởng
Với Li-chao tree truyền thống, khi chèn một đường thẳng, ta có thể gán nó cho một đoạn rộng hơn đoạn mà đường này thật sự đóng góp và min-line. Điều này không phải là vấn đề với hàm .
Tuy nhiên, khi làm việc với phép cộng, ta chỉ được phép gây ảnh hưởng lên đúng đoạn mà nó được phép gây ảnh hưởng. Để giải quyết vấn đề này, ta sử dụng lazy propagation trên Li-chao tree.
Tương tự lazy propagation trên Segment tree, với mỗi nút, ta lưu lại hàm cập nhật , đại diện cho cả đoạn mà nút quản lý đang được cộng thêm hàm . Mỗi thao tác loại tương đương với việc cộng thêm hàm cập nhật cho nút. Các giá trị chỉ được đưa xuống cây con khi ta cần xử lý đến.
Cần lưu ý, khi đi từ gốc xuống để tìm các nút cần cập nhật đối với truy vấn loại , ta cần đẩy tất cả các đường thẳng còn đang chứa ở các nút xuống bằng một thao tác chèn đoạn thẳng (trong code tham khảo gọi là thao tác pushLine). Điều này sẽ đảm bảo tất cả các đường thẳng nằm trong đoạn cần được tăng sẽ được tăng.
Bên cạnh đó, cần đảm bảo rằng khi thực hiện thao tác loại trên nút nào thì nút đó không chịu ảnh hưởng của bất kỳ giá trị lazy nào.
Code tham khảo
struct line {
ll a, b;
line() : a(0), b(0) {}
line (ll a, ll b) : a(a), b(b) {}
ll calc (ll x) { return (b == LLONG_MAX ? LLONG_MAX : a * x + b); }
ll slope() { return a; }
ll add (ll a, ll b) { // phép cộng chống tràn số
return (max(a, b) == LLONG_MAX ? LLONG_MAX : a + b);
}
void operator += (line o) {
a = add(a, o.a), b = add(b, o.b);
}
};
struct liChao {
vector<line> tr, lazy;
liChao() {}
liChao (int sz) : tr(4 * sz, line(0, LLONG_MAX)), lazy(4 * sz) {}
void apply (int k, line f) {
tr[k] += f, lazy[k] += f;
}
void pushDown (int k) {
// đẩy "hàm cập nhật" theo cập nhật tăng đoạn xuống các cây con
// để tránh ảnh hưởng của cập nhật chèn đường thẳng
if (!lazy[k].a && !lazy[k].b) return;
apply(2 * k, lazy[k]), apply(2 * k + 1, lazy[k]);
lazy[k] = line(0, 0);
}
void insertLine (line f, int k, int l, int r) {
/*
f: đường thẳng cần cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
// thực hiện cập nhật đường thẳng như Li-chao tree cơ bản, thêm
// thao tác "pushDown" để không cập nhật đè lên các cập nhật tăng đoạn
if (l == r) {
tr[k] = (f.calc(l) < tr[k].calc(l) ? f : tr[k]);
return;
}
pushDown(k);
int mid = (l + r) >> 1;
if (f.calc(mid) < tr[k].calc(mid)) swap(tr[k], f);
if (f.slope() > tr[k].slope())
insertLine(f, 2 * k, l, mid);
else if (f.slope() < tr[k].slope())
insertLine(f, 2 * k + 1, mid + 1, r);
}
void pushLine (int k, int l, int r) {
// đẩy hàm của Li-chao tree xuống các cây con để tránh
// ảnh hưởng của cập nhật tăng đoạn
int mid = (l + r) >> 1;
if (tr[k].b != LLONG_MAX) {
insertLine(tr[k], 2 * k, l, mid);
insertLine(tr[k], 2 * k + 1, mid + 1, r);
tr[k] = line(0, LLONG_MAX);
}
}
void updateInsert (int a, int b, line f, int k, int l, int r) {
/*
a..b: khoảng cần cập nhật
f: đường thẳng cần cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
// thực hiện cập nhật đoạn thẳng như Li-chao tree cơ bản, thêm
// thao tác "pushDown" để không cập nhật đè lên các cập nhật tăng đoạn
if (b < l || r < a) return;
if (a <= l && r <= b)
return insertLine(f, k, l, r), void();
pushDown(k);
int mid = (l + r) >> 1;
updateInsert(a, b, f, 2 * k, l, mid);
updateInsert(a, b, f, 2 * k + 1, mid + 1, r);
}
void updateIncrease (int a, int b, line f, int k, int l, int r) {
/*
a..b: khoảng cần cập nhật
f: đường thẳng cần cập nhật
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
// thực hiện cập nhật đoạn tương tự Segment tree, thêm thao tác
// "pushDown" và "pushLine" để không cập nhật đè lên các cập nhật trước đó
if (b < l || r < a) return;
if (a <= l && r <= b)
return apply(k, f), void();
pushDown(k), pushLine(k, l, r);
int mid = (l + r) >> 1;
updateIncrease(a, b, f, 2 * k, l, mid);
updateIncrease(a, b, f, 2 * k + 1, mid + 1, r);
}
ll query (int pos, int k, int l, int r) {
/*
pos: vị trí được truy vấn
k: nút hiện tại
l..r: khoảng mà nút quản lý
*/
ll cur = tr[k].calc(pos);
int mid = (l + r) >> 1;
if (l == r) return cur;
pushDown(k);
if (pos <= mid)
return min(cur, query(pos, 2 * k, l, mid));
else return min(cur, query(pos, 2 * k + 1, mid + 1, r));
}
};
Như vậy, ta có thể xử lý các thao tác trong độ phức tạp lần lượt là , và .
¶ Bài toán 2
Cho một mảng kích thước và truy vấn online thuộc một trong ba dạng:
- Chèn đoạn thẳng: Cho bốn số nguyên , gán với mọi .
- Tăng đoạn: Cho ba số nguyên , tăng lên đơn vị, với mọi .
- Truy vấn đoạn: Cho hai số nguyên , tính .
¶ Ý tưởng
Kết hợp với ý tưởng lazy propagation như trên, bây giờ với mỗi nút, ta lưu thêm một giá trị với là đoạn mà nút quản lý.
Lưu ý, với cách làm này, ta không thể thực hiện thao tác tăng đoạn thao dạng bậc thang, vì việc tăng như thế sẽ làm thay đổi mối quan hệ lớn bé giữa các giá trị trong đoạn được tăng. Tuy nhiên, khi đoạn được tăng cho cùng một giá trị, ta chỉ việc tăng và hệ số tự do của các đoạn thẳng nằm trong đoạn được cập nhật cho cùng một giá trị.
¶ Ứng dụng: Quy hoạch động
Đối với mỗi bài toán trong phần ứng dụng, mình khuyên các bạn đọc giả nên tự suy nghĩ lời giải cho bài toán trước khi đọc tiếp
Bên cạnh các bài toán thuần cấu trúc dữ liệu, Li-chao tree còn có một ứng dụng rất quan trọng đó là cải tiến một số thuật toán Quy hoạch động.
Thông thường, Li-chao tree có thể cải tiến các bài toán QHĐ có công thức truy hồi có dạng:
Trong đó, là các giá trị được xác định từ và các hệ số liên quan.
Để dễ hình dung hơn, chúng ta sẽ tìm hiểu các ví dụ Quy hoạch động kết hợp Li-chao tree sau.
¶ CEOI 2017: Building Bridges
Cho cột đá có độ cao và chi phí tháo dỡ là . Chọn ra một số cột đá để xây dựng cầu với chi phí là tổng bình phương của chênh lệch độ cao hai cột đá liên tiếp được chọn, cộng cho tổng chi phí tháo dỡ các cột đá không được chọn.
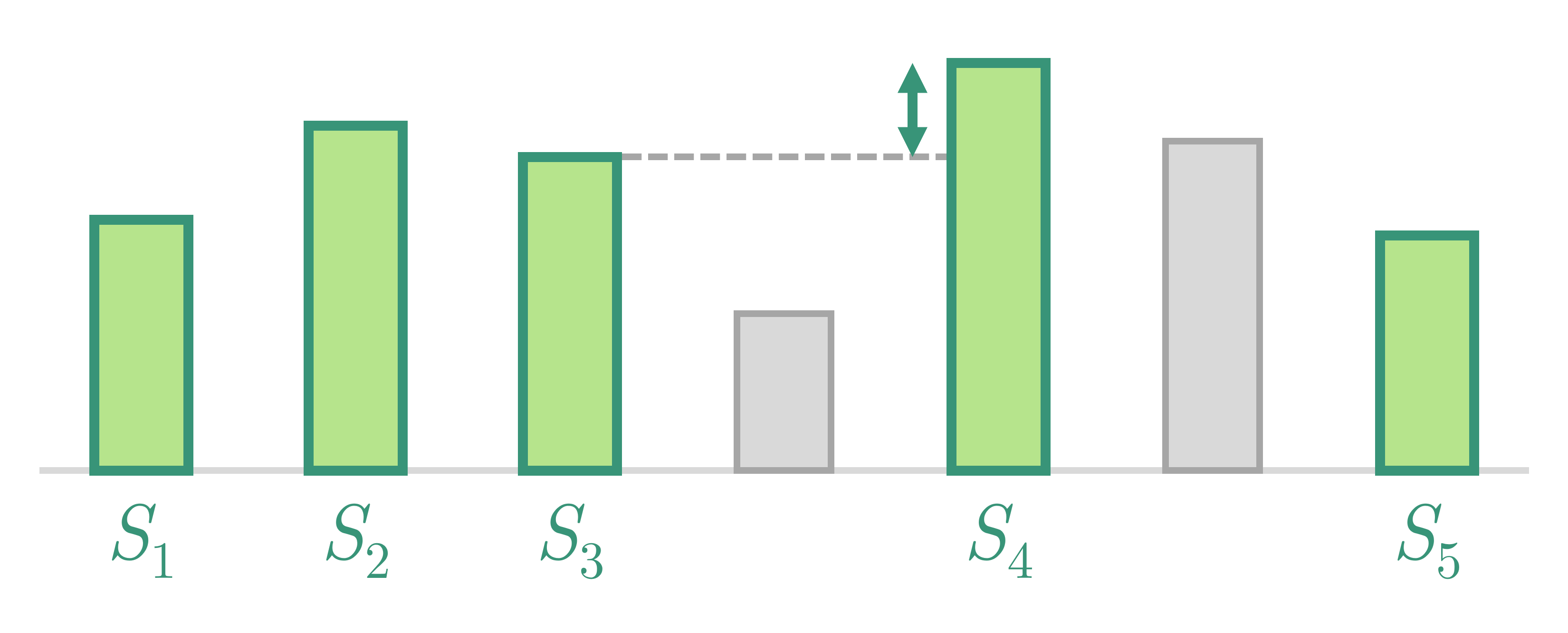
Nói cách khác, gọi là dãy các vị trí được chọn, ta có công thức tính chi phí là:
Tìm cách chọn để cực tiểu hóa chi phí xây dựng cầu, đảm bảo cột đầu tiên và cuối cùng luôn được chọn.
Giới hạn:
- .
- .
¶ Quy hoạch động
Với kiến thức Quy hoạch động cơ bản, ta có thể xây dựng thuật toán với là chi phí xây dựng cầu nhỏ nhất, trong các phương án bắt đầu từ cột đầu tiên, và kết thúc ở cột thứ . Để tính , ta thử tất cả các vị trí là cột đá được chọn nằm ngay trước , sau đó cộng thêm và chi phí để tháo dỡ các cột đá từ vị trí đến . Công thức truy hồi như sau:
Thuật toán Quy hoạch động như trên sẽ có độ phức tạp là -- chưa đủ để giải quyết bài toán.
¶ Áp dụng Li-chao tree
Với công thức truy hồi , ta có thể biến đổi thành:
với .
Ta có thể nhóm biểu thức trên thành nhóm:
Nhóm thứ ba chỉ phụ thuộc vào nên nhiệm vụ còn lại là tìm để cực tiểu hóa nhóm đầu tiên. Có thể thấy, nhóm này có dạng phương trình đường thẳng với và .
Đến đây, ta định nghĩa phương trình đường thẳng . Như vậy, công thức truy hồi được biến đổi thành:
Ta đã đưa công thức truy hồi thành dạng bài quen thuộc của Li-chao tree: Để tính , ta tìm đường thẳng có giá trị bé nhất tại điểm cộng thêm . Sau đó, thêm đường thẳng vào tập đường thẳng.
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pl;
typedef pair<int,int> pii;
typedef tuple<int,int,int> tt;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
struct line {
ll a, b;
line() : a(0), b(0) {}
line (ll a, ll b) : a(a), b(b) {}
ll calc (ll x) { return a * x + b; }
ll slope() { return a; }
};
struct liChao {
vector<line> tr;
liChao() {}
liChao (int sz) : tr(sz + 1, line(0, LLONG_MAX)) {}
void update (line f, int l, int r) {
if (l > r) return;
int mid = (l + r) >> 1;
if (l == r) {
tr[mid] = (f.calc(l) < tr[mid].calc(l) ? f : tr[mid]);
return;
}
if (f.calc(mid) < tr[mid].calc(mid)) swap(tr[mid], f);
if (f.slope() > tr[mid].slope())
update(f, l, mid - 1);
if (f.slope() < tr[mid].slope())
update(f, mid + 1, r);
}
ll query (int p, int l, int r) {
int mid = (l + r) >> 1;
ll cur = tr[mid].calc(p);
if (p == mid) return cur;
if (p < mid) return min(query(p, l, mid - 1), cur);
if (p > mid) return min(query(p, mid + 1, r), cur);
}
};
const int M = 1e6 + 1;
ll dp[M], h[M], w[M];
ll coef1 (int k) {
return -2 * h[k];
}
ll coef2 (int k) {
return dp[k] + h[k] * h[k] - w[k];
}
ll coef3 (int k) {
return h[k] * h[k] + w[k - 1];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n; cin >> n;
for (int i = 1; i <= n; i++) cin >> h[i];
for (int i = 1; i <= n; i++) {
cin >> w[i];
w[i] += w[i - 1];
}
liChao tree(M);
tree.update(line(coef1(1), coef2(1)), 0, M);
for (int i = 2; i <= n; i++) {
dp[i] = tree.query(h[i], 0, M) + coef3(i);
tree.update(line(coef1(i), coef2(i)), 0, M);
}
cout << dp[n];
return 0;
}
Như vậy, ta đã giải bài toán trong và bộ nhớ .
¶ Codeforces Round 344: Product Sum
Cho mảng gồm phần tử được đánh số từ . Thực hiện đúng một thao tác lấy một phần tử rồi đặt vào một vị trí bất kỳ (có thể là vị trí ban đầu). Đánh số lại các phần tử. Tìm cách thực hiện thao tác để cực đại hóa giá trị:
Giới hạn:
- .
- .
¶ Ý tưởng
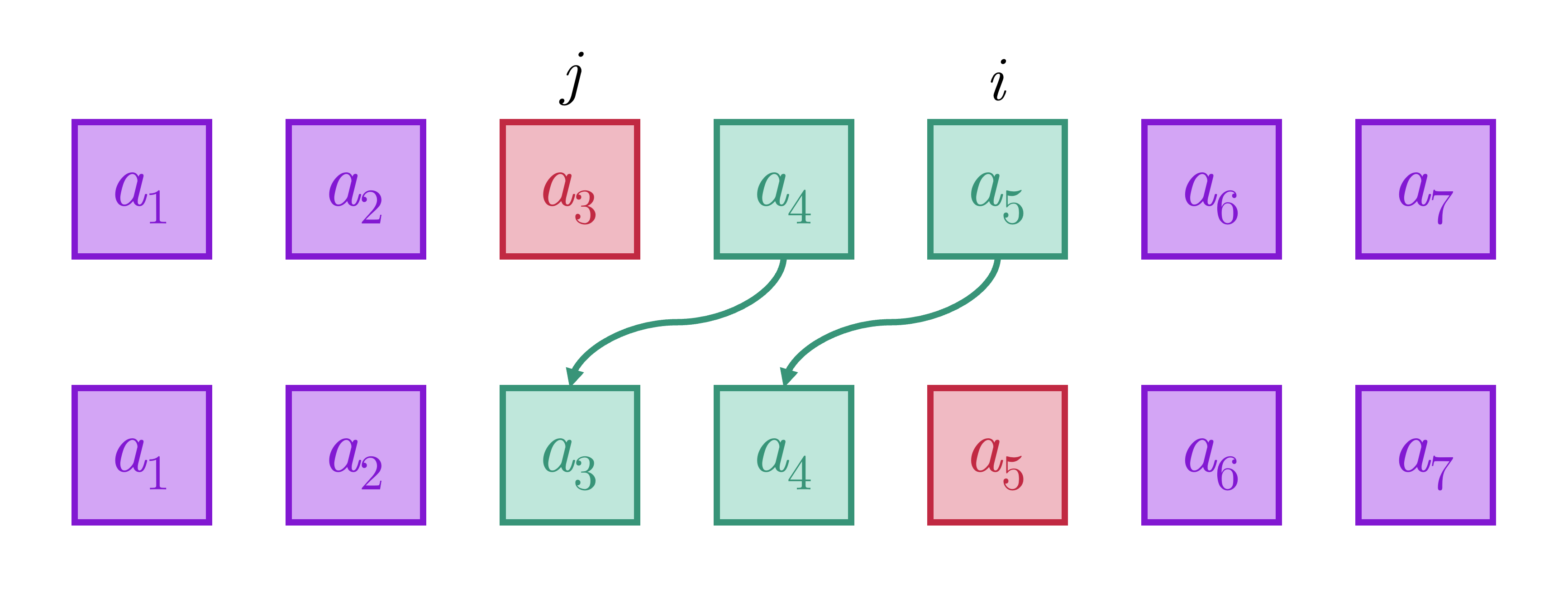
Gọi vị trí của phần tử được chọn là và vị trí mới mà nó được đặt vào là . Có hai trường hợp mà ta cần quan tâm như sau:
- Trường hợp 1: . Tức là phần tử được chọn sẽ được di chuyển sang phải. Khi đó, chỉ số của các phần tử trong đoạn sẽ được giảm đơn vị và chỉ số của biến thành .
- Trường hợp 2: . Tức là phần tử được chọn sẽ được di chuyển sang trái. Khi đó, chỉ số của các phần tử trong đoạn sẽ được tăng đơn vị và chỉ số của biến thành .
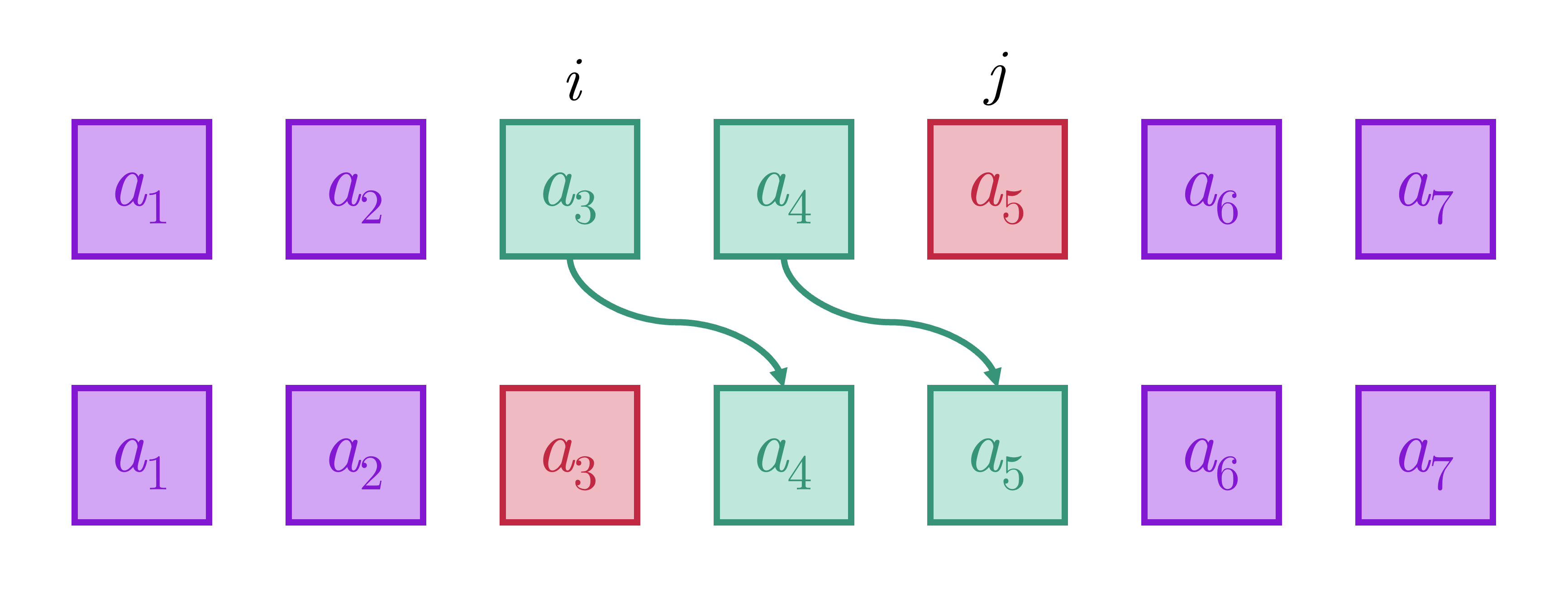
- Trường hợp 3: . Tức mảng được giữ nguyên.
Để thuật tiện cho việc tính toán, gọi:
- .
- .
- .
Như vậy, ở trường hợp 1, công thức tính giá trị mới của mảng là:
Ta nhóm biểu thức này lại thành nhóm:
Tương tự, với trường hợp 2, ta có công thức tính giá trị mới của mảng:
Ta lại nhóm biểu thức này thành nhóm:
Khi cố định , ta có thể tìm một vị trí có thể cực đại hóa phần và của cả hai biểu thức trên bằng Li-chao tree cơ bản, sau đó cộng riêng phần thứ vào.
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pl;
typedef pair<int,int> pii;
typedef tuple<int,int,int> tt;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
struct line {
ll a, b;
line() : a(0), b(LLONG_MIN) {}
line (ll a, ll b) : a(a), b(b) {}
ll calc (ll x) { return b == LLONG_MIN ? LLONG_MIN : a * x + b; }
ll slope() { return a; }
};
struct liChao {
vector<line> tr;
liChao (int sz) : tr(sz + 1) {}
void update (line cur, int l, int r) {
if (l > r) return;
if (l == r)
return tr[l] = (cur.calc(l) > tr[l].calc(l) ? cur : tr[l]), void();
int mid = (l + r) >> 1;
if (cur.calc(mid) > tr[mid].calc(mid)) swap(cur, tr[mid]);
if (cur.slope() < tr[mid].slope()) update(cur, l, mid - 1);
if (cur.slope() > tr[mid].slope()) update(cur, mid + 1, r);
}
ll query (int pos, int l, int r) {
if (l > r) return LLONG_MIN;
int mid = (l + r) >> 1;
ll cur = tr[mid].calc(pos);
if (l == r) return cur;
if (l <= pos && pos < mid)
return max(query(pos, l, mid - 1), cur);
return max(query(pos, mid + 1, r), cur);
}
// reset các giá trị của Li-chao tree
void refresh() { fill(all(tr), line(0, LLONG_MIN)); }
};
const int mn = 2e5 + 5;
ll a[mn], pre[mn], shiftRight[mn], shiftLeft[mn];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n; cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
pre[i] = pre[i - 1] + a[i] * i;
shiftRight[i] = shiftRight[i - 1] + a[i] * (i + 1);
shiftLeft[i] = shiftLeft[i - 1] + a[i] * (i - 1);
}
liChao tree(n); ll ans = pre[n];
for (int i = 1; i <= n; i++) { // xử lý các trường hợp j < i
ll best = tree.query(i, 1, n);
if (best != LLONG_MIN)
ans = max(ans, best + pre[n] - pre[i] + shiftLeft[i]);
tree.update(line(a[i], pre[i - 1] - shiftLeft[i]), 1, n);
}
tree.refresh();
for (int i = n; i >= 1; i--) { // xử lý các trường hợp j > i
ll best = tree.query(i, 1, n);
if (best != LLONG_MIN)
ans = max(ans, best + pre[n] + pre[i - 1] - shiftRight[i - 1]);
tree.update(line(a[i], shiftRight[i - 1] - pre[i]), 1, n);
}
cout << ans;
return 0;
}
¶ Educational Codeforces Round 82: Sum of Prefix Sums
Định nghĩa tổng của tổng tiền tố của một dãy , gọi là , được xác định qua công thức
Cho cây đỉnh, có trọng số đỉnh . Định nghĩa là tổng của tổng tiền tố của dãy thu được khi viết trọng số của các đỉnh trên đường đi đơn từ đến theo thứ tự. Hãy tìm .
Giới hạn:
- .
- .
¶ Biến đổi công thức tổng của tổng tiền tố
Theo định nghĩa tổng của tổng tiền tố, ta đang có một công thức . Dễ thấy, công thức đó có thể được biến đổi thành công thức sau:
Ngoài ra, nếu đã tính được và , ta có thể tính :
Để dễ hiểu hơn, ta có thể xem hình ảnh sau:
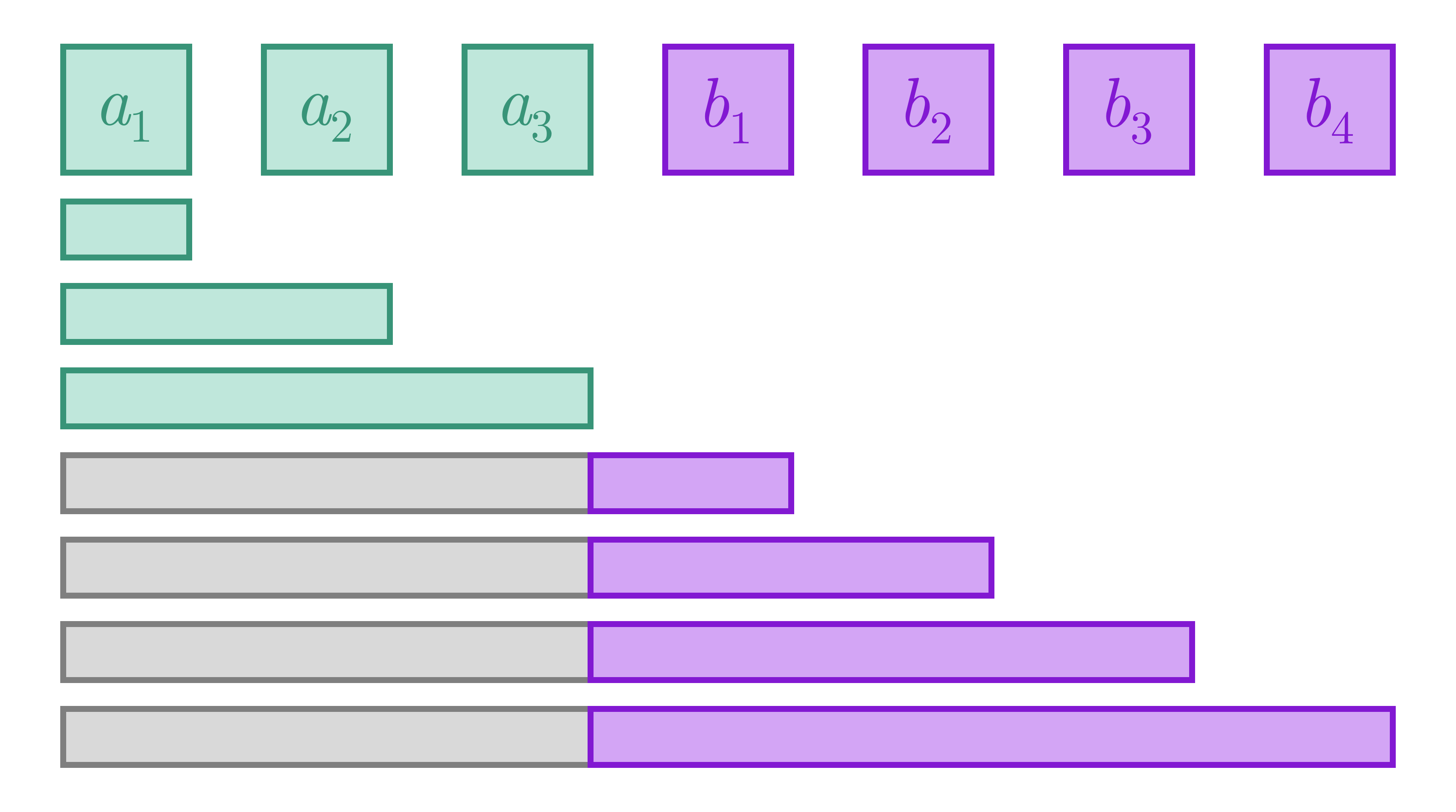
Với ý tưởng này, để tính , ta có thể tách đường đi này thành hai phần và với là nút con của nếu đi theo hướng xuống nút . Việc tính riêng rồi gộp lại thành dựa trên công thức trên sẽ thuận tiện hơn nhiều so với việc tính trực tiếp .
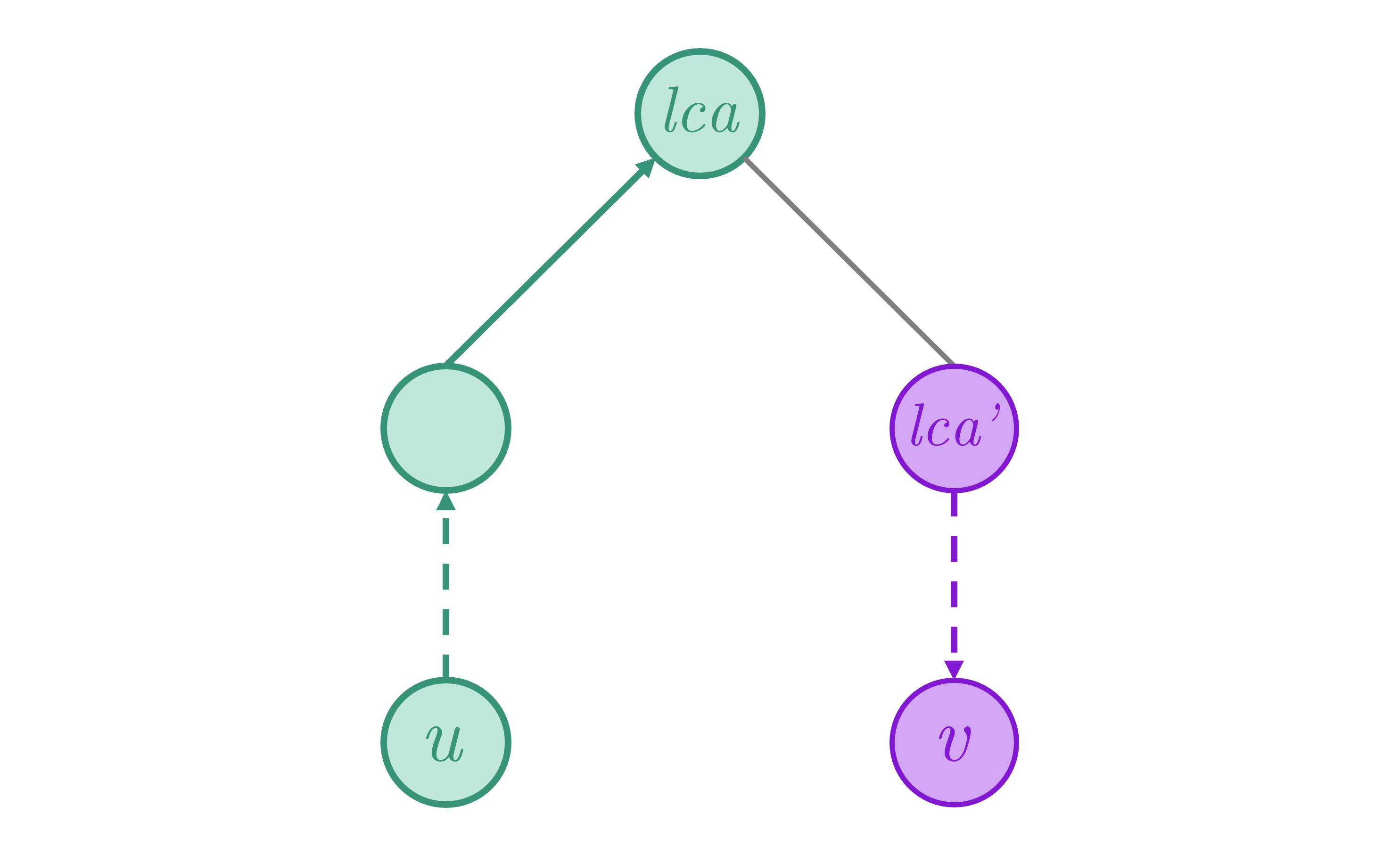
¶ Tìm đường đi tối ưu qua nút gốc
Trước khi đi đến bài toán gốc, ta cần giải một bài toán con đó là tìm đối với các đường đi đơn đi qua nút gốc . Dễ thấy, do trọng số đỉnh là các số dương nên và phải là nút lá hoặc gốc của cây. Để thuận tiện hơn cho việc tính toán, gọi:
- là tổng trọng số các đỉnh trên đường đi từ gốc xuống nút .
- là độ sâu của nút (hay số cạnh nằm trên đường đi đơn từ gốc xuống ).
- là tổng của tổng tiền tố của các nút trên đường đi đơn từ lên nút gốc.
- là tổng của tổng tiền tố của các nút trên đường đi đơn từ gốc xuống nút .
Cả bốn mảng này có thể được tính bằng một lần chạy DFS đơn giản.
Xét một nút lá nằm trong cây con của là nút con của , và một nút nằm ngoài cây con của . Ta có thể tính theo công thức:
Đến đây, ta có thể thấy, nếu cố định một nút , ta cần tìm một phương trình đường thẳng cực đại hóa giá trị tại , rồi cộng thêm . Để đảm bảo ta chỉ xét đến các nút con nằm ngoài cây con , ta cần duyệt các cây con của theo thứ tự, cập nhật các đoạn thẳng xen kẽ với truy vấn. Sau đó, ta lại duyệt các cây con của theo thứ tự ngược lại rồi thực hiện tương tự.
Ngoài ra, ta còn phải xét đường đi từ một nút lá lên nút gốc và từ nút gốc xuống một nút lá. Dễ thấy kết quả sẽ là .
¶ Tìm đường tối ưu cho mọi cặp đỉnh
Đến đây, ta có thể kết hợp thuật toán phân tách trọng tâm (centroid decomposition)[6] để tìm đường tối ưu cho mọi cặp đỉnh.
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pl;
typedef pair<int,int> pii;
typedef tuple<int,int,int> tt;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
struct line {
ll a, b;
line() : a(0), b(LLONG_MIN) {}
line (ll a, ll b) : a(a), b(b) {}
ll calc (ll x) { return (b == LLONG_MIN ? b : a * x + b); }
ll slope() { return a; }
};
const int M = 2e5;
struct liChao {
unordered_map<int,line> tr; // sử dụng tối ưu bộ nhớ kết hợp Li-chao tree trên mảng thưa
liChao() {}
void update (line cur, int l = 1, int r = M) {
if (l > r) return;
if (l == r)
return tr[l] = (cur.calc(l) > tr[l].calc(l) ? cur : tr[l]), void();
int mid = (l + r) >> 1;
if (cur.calc(mid) > tr[mid].calc(mid)) swap(cur, tr[mid]);
if (cur.slope() < tr[mid].slope()) update(cur, l, mid - 1);
if (cur.slope() > tr[mid].slope()) update(cur, mid + 1, r);
}
ll query (int pos, int l = 1, int r = M) {
if (l > r) return LLONG_MIN;
int mid = (l + r) >> 1;
ll cur = tr[mid].calc(pos);
if (l == r) return cur;
if (l <= pos && pos < mid)
return max(query(pos, l, mid - 1), cur);
else return max(query(pos, mid + 1, r), cur);
}
};
const int mn = 2e5 + 5;
ll a[mn], pre[mn], gUp[mn], gDown[mn], ans;
int sz[mn], depth[mn];
vector<int> adj[mn];
bool del[mn];
int szDfs (int u, int p) { // hàm tính kích thước từng cây con
sz[u] = 1;
for (int v : adj[u])
if (v != p && !del[v]) sz[u] += szDfs(v, u);
return sz[u];
}
int centroid (int u, int p, int sztr) { // hàm tìm kiếm trọng tâm
for (int v : adj[u])
if (v != p && !del[v] && sz[v] > sztr / 2)
return centroid(v, u, sztr);
return u;
}
void dfs (int u, int p, int d, bool start, vector<int> &leaves) { // hàm tính lại các giá trị "depth", "pre",
// "gUp", "gDown" trong cây con sau khi đặt gốc mới
depth[u] = d, pre[u] = pre[p] + a[u];
gUp[u] = a[u] * (depth[u] + 1) + gUp[p];
gDown[u] = gDown[p] + pre[u];
int child = 0;
for (int v : adj[u])
if (v != p && !del[v]) child++, dfs(v, u, d + 1, 0, leaves);
if (!child) leaves.push_back(u);
}
void solve (int root) { // hàm chia để trị trên cây
/// phần template của thuật toán phân rã trọng tâm
root = centroid(root, root, szDfs(root, root));
pre[root] = gUp[root] = gDown[root] = a[root];
vector<vector<int>> leaves(adj[root].size());
for (int i = 0; i < adj[root].size(); i++) {
int v = adj[root][i];
if (del[v]) continue;
dfs(v, root, 1, 1, leaves[i]);
}
// tìm f(u, v) lớn nhất với lca(u, v) = root
function<void(void)> calc = [&] () {
liChao tree;
for (int i = 0; i < adj[root].size(); i++) {
if (del[adj[root][i]]) continue;
for (int leaf : leaves[i]) {
ans = max({ans, gUp[leaf], gDown[leaf]}); // trường hợp lá đến gốc và từ gốc đến lá
ll best = tree.query(depth[leaf]);
if (best != LLONG_MIN)
ans = max(ans, best + gDown[leaf] - a[root] * (depth[leaf] + 1)); // trường hợp lá đến lá khác
}
for (int leaf : leaves[i])
tree.update(line(pre[leaf], gUp[leaf]));
}
return;
};
calc();
reverse(all(adj[root]));
reverse(all(leaves));
calc();
// phần template của thuật toán phân rã trọng tâm
del[root] = 1;
for (int v : adj[root])
if (!del[v]) solve(v);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n; cin >> n;
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
for (int i = 1; i <= n; i++) cin >> a[i];
solve(1);
cout << ans;
return 0;
}
Thuật toán có độ phức tạp thời gian là và bộ nhớ . Tuy nhiên, hằng số của thuật toán phân rã trọng tâm là khá lớn nên cần cài đặt khéo léo một chút để tối ưu hằng số.
¶ COMPFEST 15: Keen Tree Calculation
Cho cây đỉnh, có trọng số cạnh và truy vấn. Ở mỗi truy vấn, cho hai số nguyên , cho biết nếu trọng số của các cạnh kề với đỉnh được nhân lên lần thì đường kính của cây có độ dài là bao nhiêu. Sau mỗi truy vấn, trọng số của cây không bị thay đổi.
Giới hạn:
- .
- .
¶ Ý tưởng
Dễ thấy, do hệ số nên đường kính của cây chỉ có thể tăng. Từ đây, ta có ý tưởng là tính đường kính của cây ban đầu, sau đó, với mỗi truy vấn, tìm đường đi dài nhất đi qua nút .
Để đơn giản hóa vấn đề, ta giả sử tất cả các truy vấn có bằng nhau. Ta đặt nút này (gọi là ) làm gốc. Bây giờ, ta chỉ quan tâm bài toán nhân hệ số cho nút gốc.
¶ Giải bài toán cho nút gốc
Với mỗi nút con của , gọi là độ dài đường đi dài nhất từ xuống một nút lá bất kỳ của cây con gốc . Để tìm độ dài đường đi dài nhất đi qua , ta chọn ra tối đa nút con có lớn nhất, đáp án là tổng của hai giá trị này.
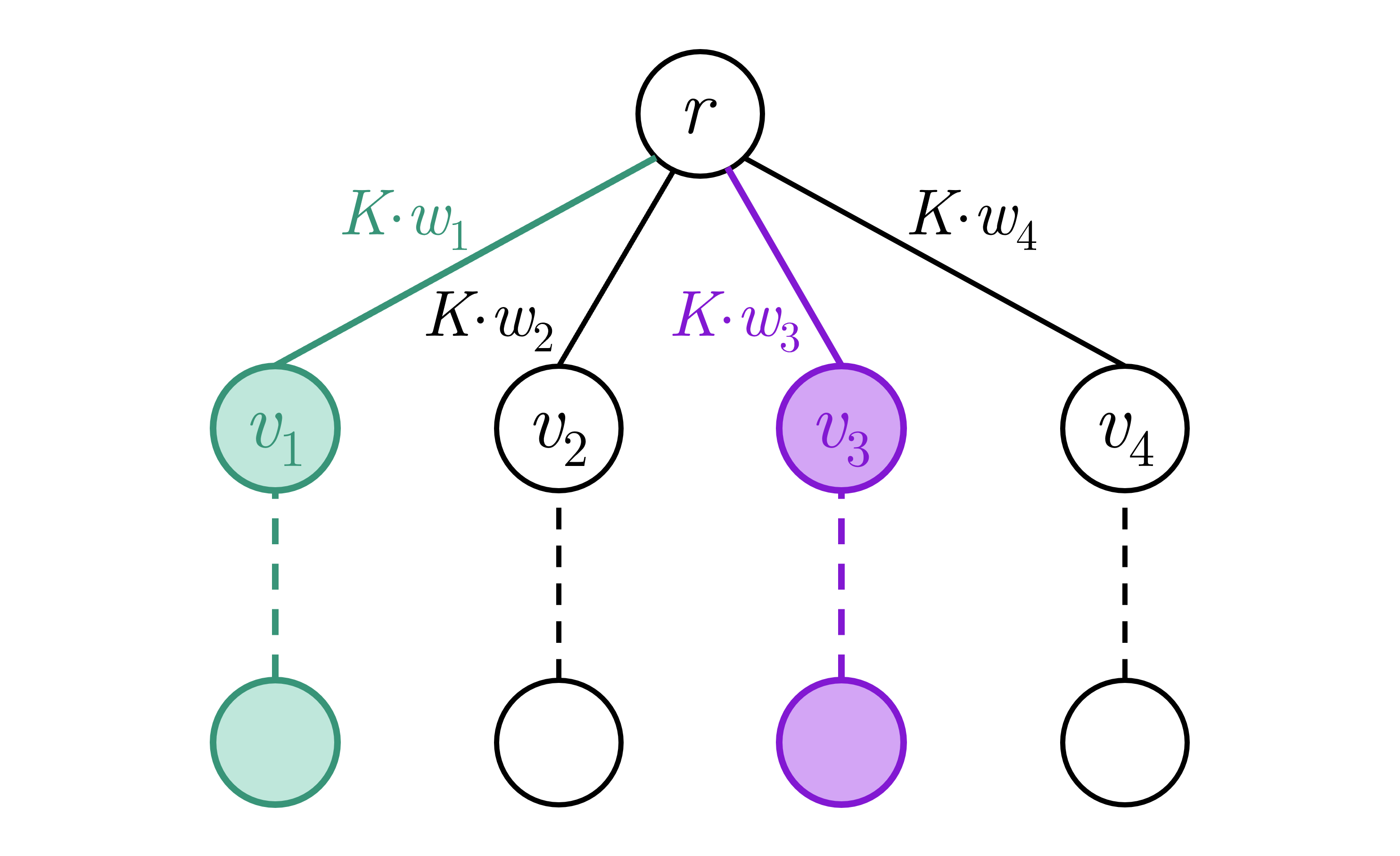
Để thực hiện nhiều truy vấn như vậy, ta để ý biểu thức trên có dạng phương trình đường thẳng. Do đó, ta có thể xây dựng Li-chao tree quản lý tập đường thẳng . Với mỗi truy vấn, ta tìm hai phương trình có giá trị lớn nhất tại . Thao tác này có thể thực hiện với biến thể Li-chao tree tìm hàm tối ưu thứ được giới thiệu ở phần trước.
¶ Giải bài toán cho cả cây
Để giải cho các nút không phải là gốc, ta có thể sử dụng kỹ thuật chuyển gốc cho Quy hoạch động trên cây[7]. Một cách làm khác là với mọi nút, ta tính:
- là độ dài đường đi dài nhất từ xuống một lá bất kỳ trong cây con của .
- là độ dài đường đi dài nhất từ ra khỏi cây con của đến một lá bất kỳ ngoài cây con của .
Sau đó, ta xử lý offline các truy vấn với ý tưởng tương tự.
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pl;
typedef pair<int,int> pii;
typedef tuple<int,int,int> tt;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
struct line {
ll a, b;
line() : a(0), b(0) {}
line (ll a, ll b) : a(a), b(b) {}
ll calc (ll x) { return a * x + b; }
ll slope() { return a; }
};
struct node {
vector<line> tr;
int mkth;
node *lpt, *rpt;
node (int mkth) : mkth(mkth), lpt(nullptr), rpt(nullptr) {}
void update (line cur, int l, int r) {
tr.push_back(cur);
if (tr.size() <= mkth * 2 - 1) return;
int mid = (l + r) >> 1;
nth_element(tr.begin(), tr.end() - 1, tr.end(),
[&] (line a, line b) { return a.calc(mid) > b.calc(mid); });
line worst = tr.back();
tr.pop_back();
if (l == r) return;
int dominantLeft = 0;
for (line it : tr)
dominantLeft += (it.slope() < worst.slope());
if (dominantLeft < mkth) {
if (lpt == nullptr) lpt = new node(mkth);
lpt->update(worst, l, mid);
}
else {
if (rpt == nullptr) rpt = new node(mkth);
rpt->update(worst, mid + 1, r);
}
}
void push (vector<ll> &cand, ll cur, int kth) {
cand.push_back(cur);
if (cand.size() > kth) {
nth_element(cand.begin(), cand.end() - 1, cand.end(), greater<ll>());
cand.pop_back();
}
}
void walk (vector<ll> &cand, int pos, int kth, int l, int r) {
for (line cur : tr) push(cand, cur.calc(pos), kth);
if (l == r) return;
int mid = (l + r) >> 1;
if (l <= pos && pos <= mid) {
if (lpt != nullptr) lpt->walk(cand, pos, kth, l, mid);
}
else {
if (rpt != nullptr) rpt->walk(cand, pos, kth, mid + 1, r);
}
}
ll query (int pos, int kth, int l, int r) {
vector<ll> cand;
walk(cand, pos, kth, l, r);
nth_element(cand.begin(), cand.end() - 1, cand.end(), greater<ll>());
return cand.back();
}
};
struct presfx {
vector<ll> pre, sfx;
int n;
presfx (vector<ll> a) : pre(a.size()), sfx(a.size()), n(a.size()) {
if (!n) return;
pre[0] = a[0], sfx[n - 1] = a[n - 1];
for (int i = 1; i < n; i++)
pre[i] = max(pre[i - 1], a[i]);
for (int i = n - 2; i >= 0; i--)
sfx[i] = max(sfx[i + 1], a[i]);
}
ll getPre (int p) { return (0 <= p && p < n ? pre[p] : 0); }
ll getSfx (int p) { return (0 <= p && p < n ? sfx[p] : 0); }
// lấy giá trị lớn nhất ngoại trừ vị trí "exc", bằng cách duy trì
// giá trị tốt nhất cho các tiền tố và hậu tố
ll query (int exc) { return max(getPre(exc - 1), getSfx(exc + 1)); }
};
const int mn = 2e5 + 5;
const int M = 1e9;
ll dpDown[mn], dpUp[mn], bestPath[mn];
vector<pii> adj[mn], qry[mn];
void dfsDown (int u, int p) {
vector<ll> a(adj[u].size());
for (int i = 0; i < adj[u].size(); i++) {
int v; ll w; tie(v, w) = adj[u][i];
if (v == p) continue;
dfsDown(v, u);
dpDown[u] = max(dpDown[u], w + dpDown[v]);
a[i] = w + dpDown[v];
}
presfx helper(a);
// ghép cạnh (u, v) với một đường đi từ u xuống nút lá khác hướng u -> v
for (int i = 0; i < adj[u].size(); i++) {
int v; ll w; tie(v, w) = adj[u][i];
if (v != p) dpUp[v] = max(dpUp[v], w + helper.query(i));
}
}
void dfsUp (int u, int p, ll toParent) {
node tree(2);
for (auto [v, w] : adj[u])
if (v != p) tree.update(line(w, dpDown[v]), 1, M);
if (u != p) { // u không phải nút gốc
dpUp[u] = max(dpUp[u], toParent + dpUp[p]);
tree.update(line(toParent, dpUp[u] - toParent), 1, M);
}
// trả lời các truy vấn gắn với nút u
for (auto [multiplier, id] : qry[u]) {
if (adj[u].size() == 1) bestPath[id] = tree.query(multiplier, 1, 1, M);
else bestPath[id] = tree.query(multiplier, 1, 1, M) + tree.query(multiplier, 2, 1, M);
}
for (auto [v, w] : adj[u])
if (v != p) dfsUp(v, u, w);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n; cin >> n;
for (int i = 1; i < n; i++) {
int u, v, w; cin >> u >> v >> w;
adj[u].emplace_back(v, w);
adj[v].emplace_back(u, w);
}
int q; cin >> q;
for (int i = 0; i < q; i++) {
int u, k; cin >> u >> k;
qry[u].emplace_back(k, i);
}
dfsDown(1, 1);
dfsUp(1, 1, 0);
ll diameter = 0;
for (int i = 1; i <= n; i++)
diameter = max(diameter, dpDown[i] + dpUp[i]);
for (int i = 0; i < q; i++)
cout << max(diameter, bestPath[i]) << "\n";
return 0;
}
Thuật toán có độ phức tạp thời gian và bộ nhớ là .
¶ Ứng dụng: Các bài tập thuần cấu trúc dữ liệu
¶ Codeforces Round 545: Train Car Selection
Cho một mảng gồm phần tử được đánh số từ . Ban đầu, các phần tử của có giá trị là . Thực hiện thao tác trên mảng thuộc trong loại như sau:
- Cho số nguyên , thêm phần tử có giá trị vào đầu mảng . Sau thao tác này, các phần tử sẽ được đánh số lại.
- Cho số nguyên , thêm phần tử có giá trị vào cuối mảng .
- Cho hai số nguyên , thực hiện tăng lên đơn vị với mọi phần tử trong mảng .
Sau mỗi thao tác, trong các phần tử có giá trị nhỏ nhất, tìm phần tử có chỉ số nhỏ nhất.
Giới hạn:
- .
- .
- .
- Đảm bảo các giá trị của mảng không vượt quá .
¶ Xử lý chỉ số
Để tránh phải xử lý chỉ số, lưu hai biến và ban đầu có giá trị là và . Với thao tác loại 1, các phần tử được thêm vào sẽ có chỉ số từ đến và biến sẽ được giảm đơn vị. Tương tự với thao tác loại 2, các phần tử được thêm vào có chỉ số từ đến và biến sẽ được tăng đơn vị.
Như vậy, thao tác loại 3 sẽ được biến đổi thành tăng lên đơn vị với .
¶ Ý tưởng
Thoạt đầu, bài toán có vẻ yêu cầu sử dụng một cấu trúc dữ liệu hỗ trợ tăng đoạn theo dạng bậc thang. Tuy nhiên, ta có thể biến đổi một chút để biến thành một bài toán đơn giản hơn nhiều.
Một nhận xét quan trọng đó là, với mỗi nhóm các phần tử được thêm vào trong cùng một thao tác, chỉ có phần tử đầu tiên có thể đóng góp vào đáp án. Lý do là vì ở thao tác loại 3, hệ số luôn dương nên các phần tử có chỉ số càng lớn sẽ càng tăng mạnh. Như vậy, ta chỉ cần quan tâm vị trí khác nhau.
Xét các phần tử có sẵn trong mảng từ ban đầu, giả sử ta đã thực hiện được thao tác loại 3. Gọi là giá trị tại thời điểm thực hiện thao tác loại 3 thứ . Giá trị của là:
Biến đổi công thức lại thành:
Để áp dụng công thức này cho các phần tử được thêm vào mảng sau, ta cần tìm cách "triệt tiêu" ảnh hưởng của các thao tác loại 3 được thực hiện trước đó. Cụ thể, với phần tử được thêm vào tại thời điểm đã thực hiện được thao tác loại 3, ta có công thức xác định như sau:
Biến đổi công thức lại và nhóm thành phần:
Lưu ý
Biến phụ thuộc vào nên ta chỉ xét tính phụ thuộc của biến và .
Đến đây, ta thấy hai phần đầu tiên tạo thành một phương trình đường thẳng. Như vậy, sau thao tác loại 3 thứ , giá trị nhỏ nhất sẽ là giá trị của phương trình đường thẳng được cực tiểu hóa tại điểm . Từ đây, có thể sử dụng Sparse Li-chao tree để thực hiện các truy vấn.
¶ Thuật toán
Đặt và , tính các thao tác đến thời điểm hiện tại, và là tập đoạn thẳng được quản lý bởi Sparse Li-chao tree. Ta xử lý các thao tác như sau:
- Thao tác loại 1: Giảm xuống đơn vị và thêm phương trình vào tập đường thẳng.
- Thao tác loại 2: Thêm phương trình vào tập đường thẳng rồi tăng lên đơn vị.
- Thao tác loại 3: Tăng lên đơn vị và tăng lên đơn vị.
Sau mỗi thao tác, tìm . Để tìm chỉ số tương ứng, ta lưu mỗi hàm dưới dạng cặp giá trị , ưu tiên cực tiểu hóa giá trị của hàm, sau đó mới cực tiểu hóa giá trị của .
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pl;
typedef pair<int,int> pii;
typedef tuple<int,int,int> tt;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
const int M = 5e14;
struct line {
ll a, b;
line() : a(0), b(0) {}
line (ll a, ll b) : a(a), b(b) {}
pl calc (ll x) { return make_pair(a * x + b, a); }
ll slope() { return a; }
};
struct node {
line tr;
node *lpt, *rpt;
node() : tr(0, LLONG_MAX), lpt(nullptr), rpt(nullptr) {}
ll divi (ll a, ll b) {
return a / b - ((a ^ b) < 0 && a % b);
}
void update (line cur, ll l = -M, ll r = M) {
if (l == r) {
if (cur.calc(l) < tr.calc(l)) tr = cur;
return;
}
ll mid = divi(l + r, 2);
if (cur.calc(mid) < tr.calc(mid)) swap(cur, tr);
if (cur.slope() > tr.slope()) {
if (lpt == nullptr) lpt = new node();
lpt->update(cur, l, mid);
}
else if (cur.slope() < tr.slope()) {
if (rpt == nullptr) rpt = new node();
rpt->update(cur, mid + 1, r);
}
}
pl query (ll x, ll l = -M, ll r = M) {
pl cur = tr.calc(x);
ll mid = divi(l + r, 2);
if (l == r) return cur;
if (x <= mid) {
if (lpt == nullptr) return cur;
return min(cur, lpt->query(x, l, mid));
}
else {
if (rpt == nullptr) return cur;
return min(cur, rpt->query(x, mid + 1, r));
}
}
};
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, q; cin >> n >> q;
ll head = 1, tail = n, P = 0, T = 0;
node tree; tree.update(line(head, 0));
while (q--) {
int type; cin >> type;
if (type == 1) {
int k; cin >> k;
head -= k;
tree.update(line(head, - head * P - T));
}
else if (type == 2) {
int k; cin >> k;
tree.update(line(tail + 1, - (tail + 1) * P - T));
tail += k;
}
else {
int b, s; cin >> b >> s;
P += s, T += b - head * s;
}
ll best; int pos; tie(best, pos) = tree.query(P);
cout << pos - head + 1 << " " << best + T << "\n";
}
return 0;
}
Thuật toán có độ phức tạp thời gian và bộ nhớ là .
¶ IOI 2005: Mountain
Cho mảng gồm phần tử, ban đầu toàn bộ phần tử có giá trị bằng . Thực hiện thao tác:
- Cho ba số nguyên , gán với mọi .
- Cho số nguyên . Gọi mảng là mảng tổng tiền tố của , tìm vị trí lớn nhất sao cho .
Giới hạn:
- .
- .
- .
- .
- .
¶ Ý tưởng
Thay vì thao tác trên mảng , ta sẽ thao tác trên mảng , tức mảng tổng tiền tố của . Lúc này, thao tác loại 1 sẽ được biến đổi thành một thao tác gán phương trình đường thẳng và tăng/giảm một đoạn cho cùng một giá trị:
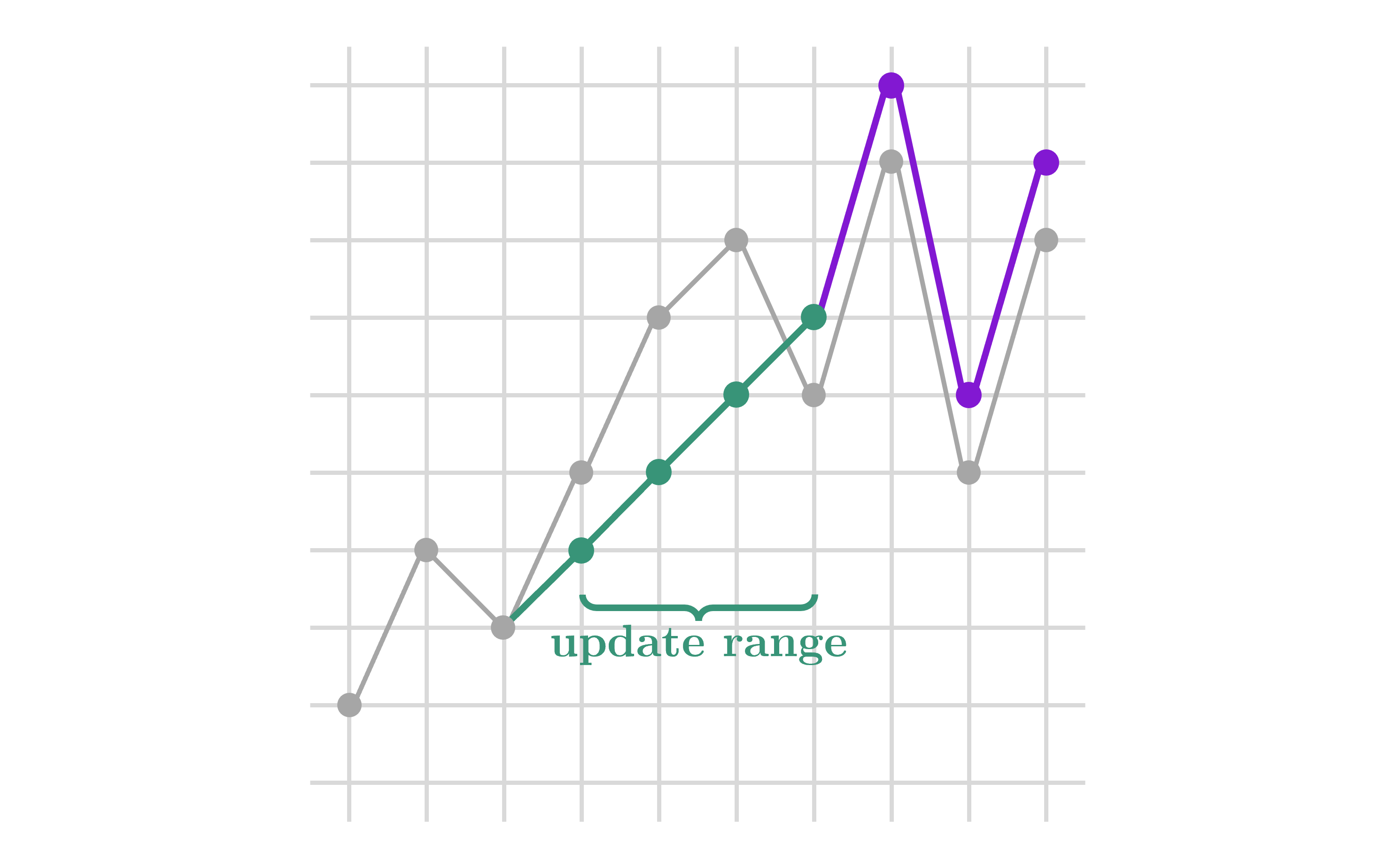
Như vậy, ta cần một cấu trúc dữ liệu hỗ trợ các thao tác sau:
- Gán phương trình đường thẳng: Cho bốn số nguyên , gán với mọi .
- Tăng đoạn: Cho ba số nguyên , tăng lên đơn vị với mọi .
- Truy vấn : Cho hai số nguyên , tính .
Cả ba thao tác đều có thể được xử lý bằng Sparse Li-chao tree với Lazy propagation (Extended Li-chao tree cài đặt bằng con trỏ).
Với thao tác loại 3, ta có thể chặt nhị phân trên thao tác tìm truy vấn . Tuy nhiên, nếu giới hạn đủ chặt chẽ thì độ phức tạp sẽ là không đủ. Do đó, ta cần áp dụng một thuật toán tương tự Walk on Segment tree[8] cho thao tác này.
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll,ll> pl;
typedef pair<int,int> pii;
typedef tuple<int,int,int> tt;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
struct line {
int a, b;
line() : a(0), b(0) {}
line (int a, int b) : a(a), b(b) {}
int calc (int x) { return a * x + b; }
bool operator != (const line &o) const {
return a != o.a || b != o.b;
}
bool operator == (const line &o) const {
return a == o.a && b == o.b;
}
};
const line init(INT_MIN, INT_MIN);
struct node {
int tr, lazy;
line asgn;
node *lpt, *rpt;
node() : tr(0), lazy(0), asgn(init), lpt(nullptr), rpt(nullptr) {}
int get (int l, int r) {
if (asgn == init) return lazy + tr;
return lazy + max(asgn.calc(l), asgn.calc(r));
}
void pushDown (int l, int r, int mid) {
if (lpt == nullptr) lpt = new node();
if (rpt == nullptr) rpt = new node();
bool change = 0;
if (asgn != init)
lpt->asgn = rpt->asgn = asgn, lpt->lazy = rpt->lazy = 0, asgn = init, change = 1;
if (lazy)
lpt->lazy += lazy, rpt->lazy += lazy, lazy = 0, change = 1;
if (change)
tr = max(lpt->get(l, mid), rpt->get(mid + 1, r));
}
void assignLine (int a, int b, line cur, int l, int r) {
/*
a..b: khoảng cần cập nhật
cur: đường thẳng cần cập nhật
l..r: khoảng mà nút quản lý
*/
if (b < l || r < a) return;
if (a <= l && r <= b) {
asgn = cur, lazy = 0;
return;
}
int mid = (l + r) >> 1; pushDown(l, r, mid);
lpt->assignLine(a, b, cur, l, mid);
rpt->assignLine(a, b, cur, mid + 1, r);
tr = max(lpt->get(l, mid), rpt->get(mid + 1, r));
}
void addConstant (int a, int b, int delta, int l, int r) {
/*
a..b: khoảng cần cập nhật
delta: giá trị cần nhập nhật
l..r: khoảng mà nút quản lý
*/
if (b < l || r < a) return;
if (a <= l && r <= b) {
lazy += delta;
return;
}
int mid = (l + r) >> 1; pushDown(l, r, mid);
lpt->addConstant(a, b, delta, l, mid);
rpt->addConstant(a, b, delta, mid + 1, r);
tr = max(lpt->get(l, mid), rpt->get(mid + 1, r));
}
int walk (int targ, int l, int r) {
/*
targ: tìm vị trí nhỏ nhất > targ
l..r: khoảng mà nút quản lý
*/
if (l == r) return l;
int mid = (l + r) >> 1; pushDown(l, r, mid);
if (lpt->get(l, mid) > targ) return lpt->walk(targ, l, mid);
return rpt->walk(targ, mid + 1, r);
}
int query (int pos, int l, int r) {
/*
pos: vị trí được truy vấn
l..r: khoảng mà nút quản lý
*/
if (l == r) return get(l, r);
if (asgn != init) return asgn.calc(pos) + lazy;
int mid = (l + r) >> 1;
if (l <= pos && pos <= mid)
return lazy + (lpt == nullptr ? 0 : lpt->query(pos, l, mid));
if (mid < pos && pos <= r)
return lazy + (rpt == nullptr ? 0 : rpt->query(pos, mid + 1, r));
}
};
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n; cin >> n;
node tree;
char type;
while (cin >> type) {
if (type == 'E') return 0;
if (type == 'I') {
int a, b, D; cin >> a >> b >> D;
int curL = (a > 1 ? tree.query(a - 1, 1, n) : 0), curR = tree.query(b, 1, n);
tree.assignLine(a, b, line(D, curL - D * (a - 1)), 1, n);
if (b < n)
tree.addConstant(b + 1, n, tree.query(b, 1, n) - curR, 1, n);
}
else {
int h; cin >> h;
cout << (tree.get(1, n) <= h ? n : tree.walk(h, 1, n) - 1) << "\n";
}
}
return 0;
}
Thuật toán có độ phức tạp thời gian và bộ nhớ là .
¶ Phụ lục
¶ Bài tập ứng dụng
¶ Li-chao tree và các biến thể cơ bản
- Library Checker: Segment Add Get Min
- CEOI 2017: Building Bridges
- Codeforces Round 526: The Fair Nut and Rectangles
- Codeforces Round 189: Kalila and Dimna in the Logging Industry
- CSES: Houses and Schools
- Codeforces Round 334: Product Sum
- CEOI 2009: Harbingers
- Codeforces Round 545: Train Car Selection
- Codeforces Round 463: Escape Through Leaf
- Codeforces Beta Round 75: Igloo Skyscraper
- Educational Codeforces Round 11: Bear and Bowling 4
- AtCoder: Contest with Drinks Hard
- Educational Codeforces Round 82: Sum of Prefix Sums
- APIO 2010: Commando
- Codeforces Beta Round 64: Professor's task
¶ Li-chao tree tìm hàm tối ưu thứ
¶ Extended Li-chao tree
- IOI 2005: Mountain
- Atcoder Beginner Contest 177: I hate Shortest Path Problem
- NOI 2020: Progression
- IOI 2018: Meetings
- Library Checker: Range Linear Add Range Min