¶ Cặp ghép cực đại trên đồ thị hai phía
Author:
- Trần Quang Trường - Trường đại học Công nghệ Thông tin - ĐHQGHCM.
Reviewers:
- Nguyễn Quang Minh - Michigan State University, USA
- Lê Minh Hoàng - Đại học Khoa học Tự nhiên, ĐHQG-HCM
- Nguyễn Tấn Minh - THPT Chuyên Lê Hồng Phong, TPHCM
Cặp ghép cực đại trên đồ thị hai phía là một trong những bài toán thuộc lớp bài toán về đồ thị. Bài viết sau đây sẽ giới thiệu nội dung cơ bản của bài toán và các thuật toán liên quan.
¶ Một số kiến thức cần biết
Trước khi đọc bài viết này, bạn cần trang bị kiến thức về các chủ đề sau:
¶ Củng cố kiến thức
Để hiểu rõ các định nghĩa và lý thuyết được sử dụng trong bài viết, chúng ta sẽ cùng tìm hiểu một số vấn đề sau:
¶ Cặp ghép
Cho một độ thị vô hướng gồm đỉnh và cạnh. Một tập cạnh được gọi là cặp ghép nếu không có đỉnh nào xuất hiện trong nhiều hơn một cạnh của
Ngoài ra, ta gọi một cạnh là một cạnh tự do nếu nó không xuất hiện trong tập cạnh ; một đỉnh là một đỉnh tự do nếu không thuộc bất kỳ cạnh nào trong tập cạnh .
Ví dụ, đồ thị sau mô tả một cặp ghép với các đỉnh và cạnh được tô màu xanh dương là cạnh và đỉnh tự do:
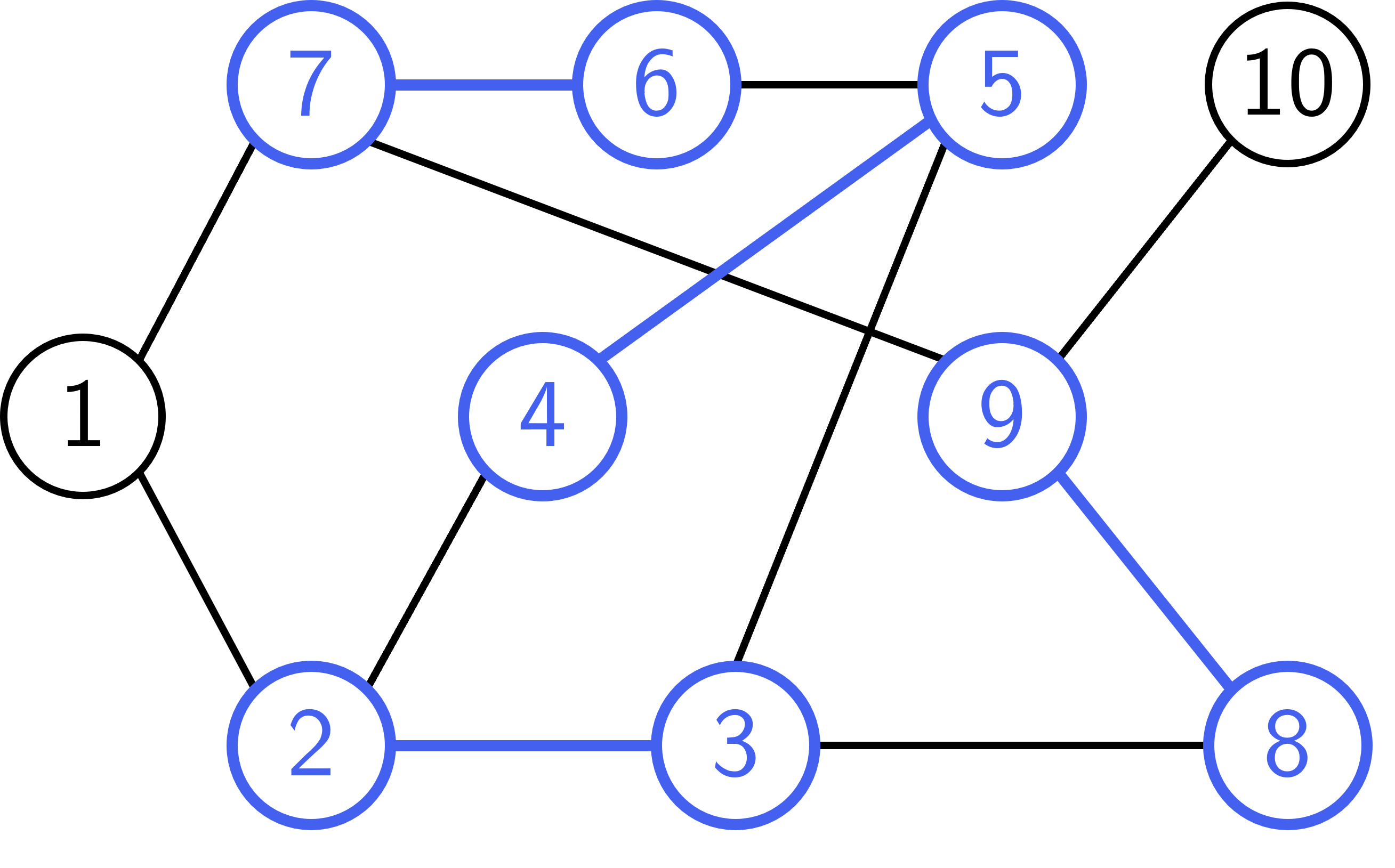
Hình 1: Cặp ghép trên một đồ thị vô hướng
¶ Đường tăng luồng
Một đường tăng luồng là một đường đi bắt đầu và kết thúc bằng cạnh tự do, đồng thời hai đỉnh đầu mút của đường đi cũng là các đỉnh tự do.
Đường đi là một đường tăng luồng tương ứng với cặp ghép , ta có một số tính chất cơ bản sau:
- Mỗi cạnh thuộc đường đi thuộc tập cạnh . .
- là các đỉnh tự do và là các đỉnh được ghép.
- Các cạnh luân phiên giữa trong và ngoài . và .
Có cạnh được ghép và cạnh tự do. - .
Ví dụ, với đồ thị và cặp ghép như trên, ta có đường đi là một đường tăng luồng:
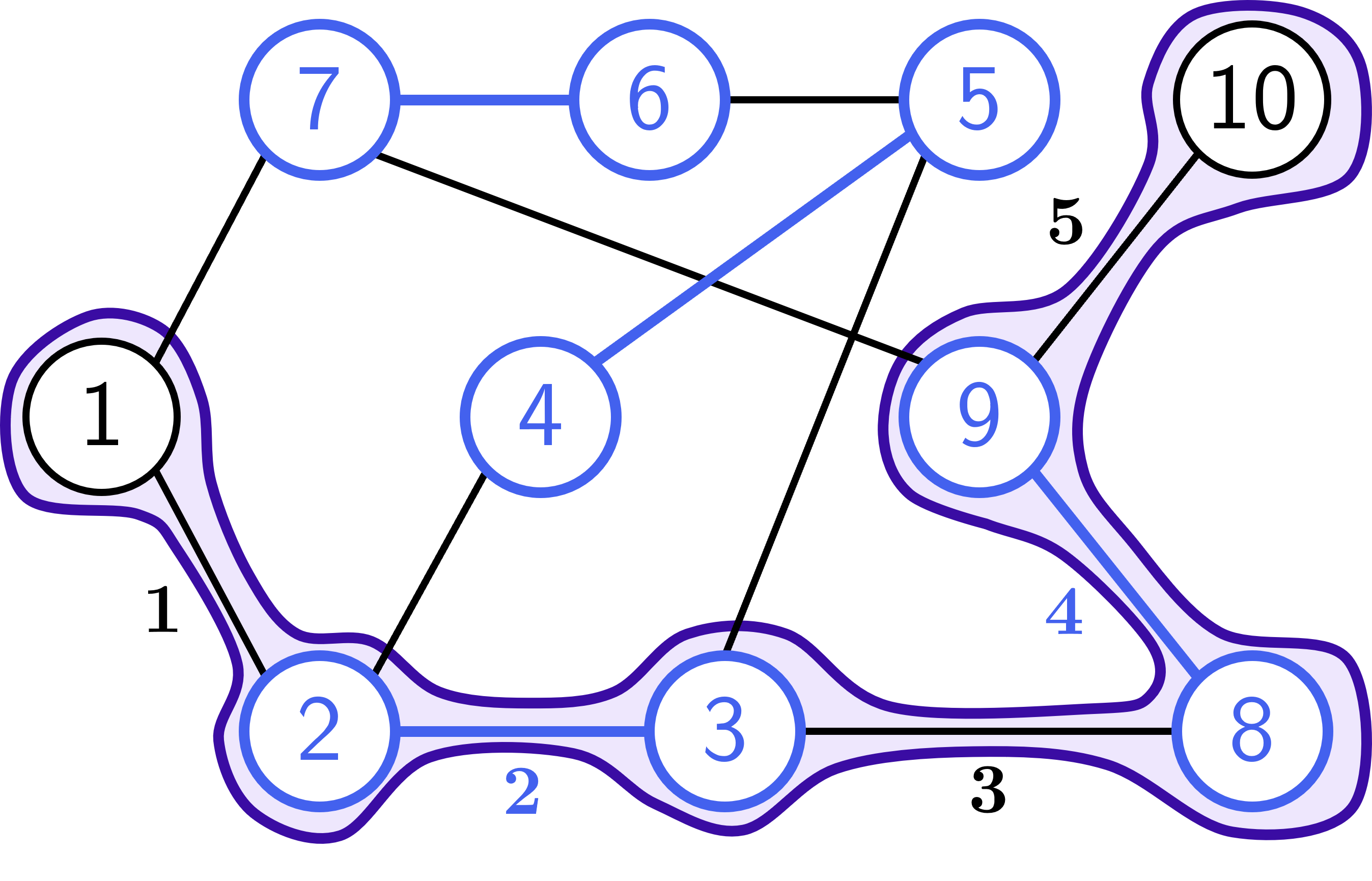
Hình 2: Đường tăng luồng
Bổ đề 1: Nếu là một cặp ghép và là một đường tăng luồng tương ứng với , thì:
là một cặp ghép và .
Chứng minh
Chứng minh 1: là một cặp ghép.
- Vì là một đường tăng luồng, nó bắt đầu và kết thúc tại các đỉnh tự do, đồng thời luân phiên giữa các cạnh trong và ngoài . Khi thực hiện tại mỗi đỉnh trong vẫn thuộc tối đa một cạnh trong , do đó đảm bảo rằng là một cặp ghép hợp lệ.
Chứng minh 2: .
- Do có số cạnh lẻ và bắt đầu, kết thúc tại các đỉnh chưa ghép, số cạnh mới thêm vào () luôn nhiều hơn số cạnh bị loại bỏ () đúng một đơn vị. Do đó, .
Hình ảnh minh họa của cặp ghép được tạo từ cặp ghép và đường tăng luồng như hình trên:
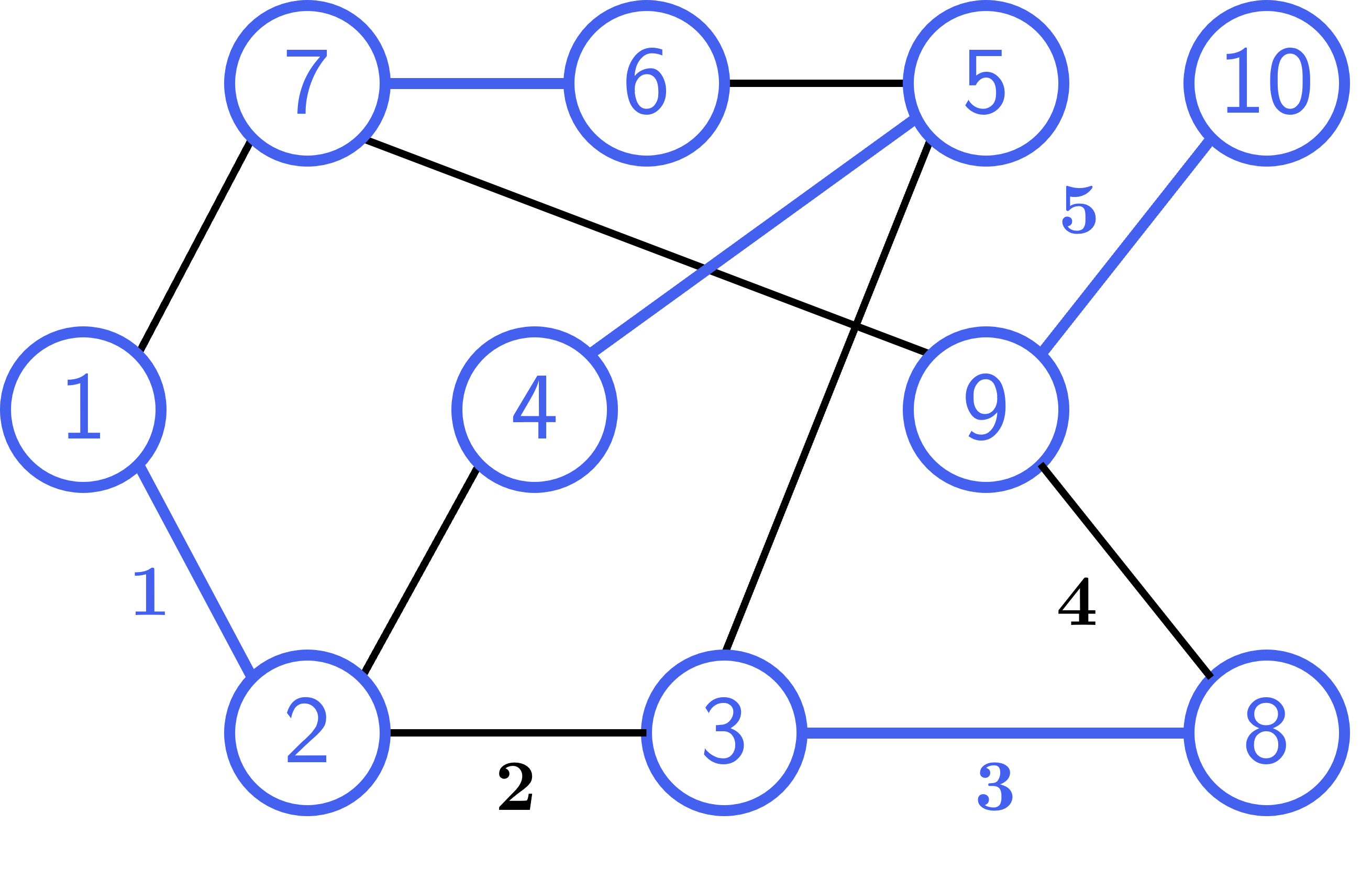
Hình 3: Cặp ghép sau khi thực hiện phép hiệu đối xứng với đường tăng luồng
¶ Bài toán
Cho một đồ thị hai phía vô hướng:
Tập đỉnh là tập bên trái của đồ thị.
Tập đỉnh là tập bên phải của đồ thị.
Tập cạnh .
Hãy tìm cặp ghép cực đại của đồ thị .
Ràng buộc: .
¶ Thuật toán luồng cực đại
Tất cả những bài toán có thể giải được bằng cặp ghép cực đại trên đồ thị hai phía thì đều có thể giải bằng luồng cực đại.
¶ Xây dựng đồ thị luồng
Đầu tiên, ta nối đỉnh nguồn tới các đỉnh thuộc tập với dung lượng là .
Sau đó, với mỗi cạnh , ta nối đỉnh tới đỉnh với dung lượng là .
Cuối cùng, ta nối các đỉnh thuộc tập tới đỉnh thu với dung lượng là .
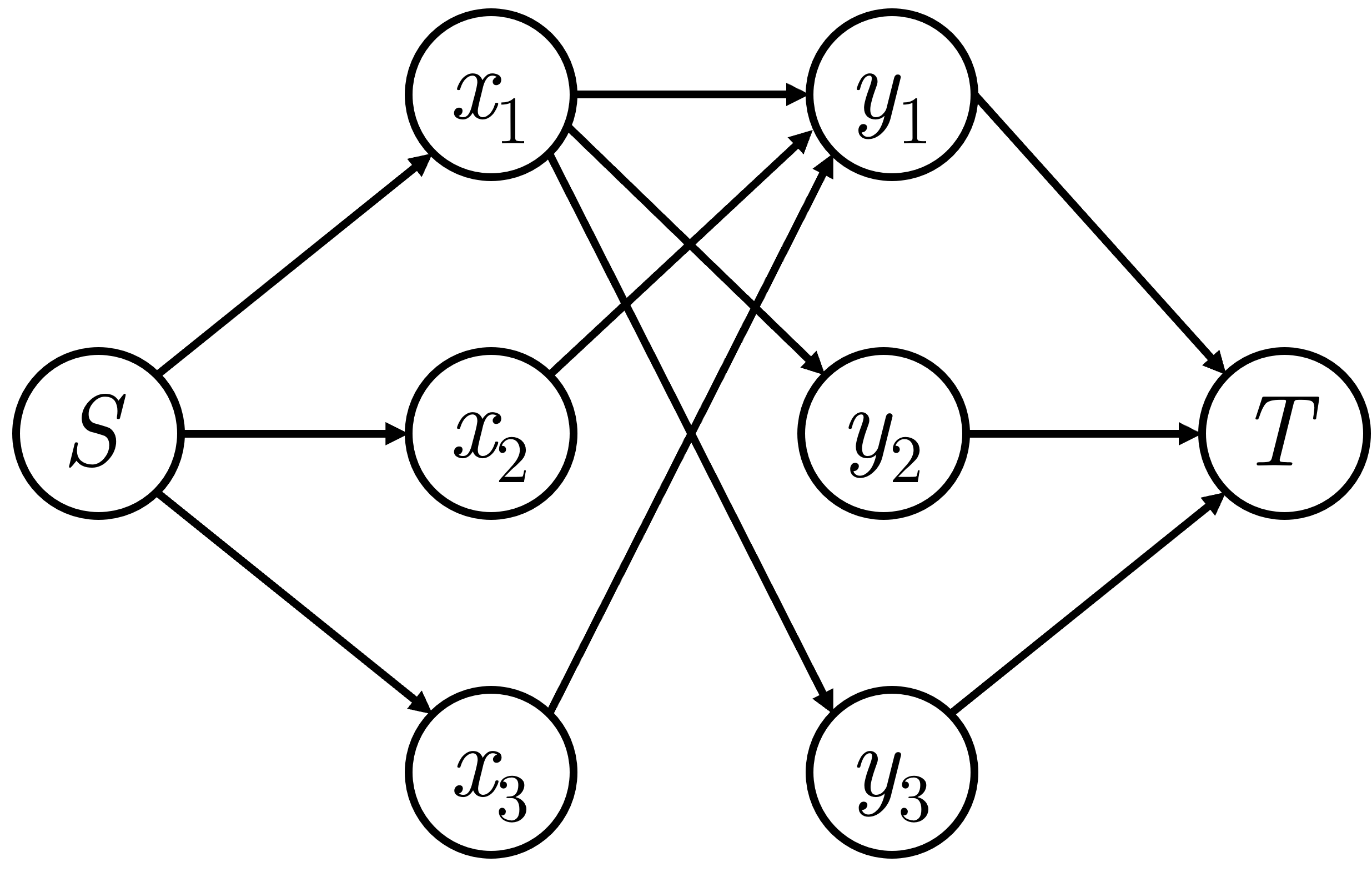
Hình 4: Đồ thị luồng cho bài toán cặp ghép cực đại
Hình minh hoạ đồ thị luồng của đồ thị có tập
Cặp ghép cực đại sẽ bằng luồng cực đại đi từ đỉnh nguồn tới đỉnh thu .
¶ Cài đặt
Có rất nhiều thuật toán luồng cực đại nhưng chung quy đều phải có hai hàm addEdge(u, v, cap) (Thêm cạnh với dung lượng ) và calc(s, t) (Trả về luồng cực đại đi từ tới ).
Ta dễ dàng xây dựng đồ thị luồng với đoạn mã giả dưới đây:
// Quy ước S = 0 là đỉnh source, T = M + N + 1 là đỉnh sink.
// Các đỉnh 1..M là các đỉnh thuộc tập X.
// Các đỉnh M+1..M+N là các đỉnh thuộc tập Y.
S = 0, T = M + N + 1
for i=1..M:
addEdge(S, i, 1)
foreach (u, v) in E:
addEdge(u, M + v, 1)
for i=1..N:
addEdge(M + i, T, 1)
return calc(S, T)
¶ Độ phức tạp
Độ phức tạp của bài toán tuỳ thuộc vào thuật toán luồng cực đại đã sử dụng. Ví dụ:
- Trong đồ thị có dạng mạng đơn vị, thuật toán Dinic sẽ giải quyết bài toán với độ phức tạp .
Để hiểu rõ tại sao có độ phức tạp này, độc giả có thể tìm hiểu thêm về thuật toán Dinic trong mạng đơn vị. - Do giá trị của luồng cực đại không quá nên với thuật toán Edmonds-Karp ta đạt độ phức tạp thuật toán là hay
¶ Thuật toán Kuhn
Dù các thuật toán luồng cực đại có thể đạt độ phức tạp tốt như thuật toán Dinic nhưng các thuật toán về luồng cực đại chung quy đều rất khó trong việc cài đặt. Với một hàm gọi đệ quy ngắn gọn cùng vài vòng lặp for đơn giản, thuật toán Kuhn giúp ta cải thiện thời gian cài đặt thuật toán.
¶ Thuật toán
Mô hình thuật toán Kuhn hoạt động như sau:
Bước 1: Tìm kiếm đường tăng luồng.
Bước 2: Cập nhật cặp ghép dựa vào đường tăng luồng tìm được.
Bước 3: Kết thúc thuật toán nếu không còn đường tăng luồng nào nữa. Ngược lại, quay lại bước .
¶ Chứng minh tính đúng đắn của thuật toán
Vậy tại sao đồ thị đạt cực đại khi không tìm được thêm đường tăng luồng nào nữa? Câu trả lời nằm ở định lý Berge.
Định lý phát biểu: Cặp ghép đạt cực đại khi và chỉ khi đồ thị không còn chứa đường tăng luồng nào tương ứng với .
Chứng minh
Chứng minh 1: Nếu đồ thị tồn tại một đường tăng luồng tương ứng với cặp ghép , thì cặp ghép không đạt cực đại.
-
Xét một đồ thị tồn tại một đường tăng luồng tương ứng với cặp ghép .
Theo Bổ đề 1, ta có , với .
-
Do đó, cặp ghép không phải là cặp ghép cực đại. Giả thiết được chứng minh.
Chứng minh 2: Nếu cặp ghép của đồ thị chưa đặt cực đại, thì đồ thị vẫn còn đường tăng luồng.
-
Xét đồ thị có cặp ghép hiện tại chưa đạt cực đại và cặp ghép cực đại .
Xét đồ thị gồm tập cạnh . Mỗi đỉnh của đồ thị có thể có tối đa cạnh chứa nó, gồm một cạnh trong và một cạnh trong . Do đó, mỗi thành phần liên thông của đồ thị sẽ có dạng một chu trình chẵn đi xen kẽ các cạnh trong và trong hoặc sẽ có dạng một đường đi đơn xen kẽ các cạnh trong và trong .
Vì nên tồn tại ít nhất một thành phần liên thông có dạng đường đi của phải bắt đầu và kết thúc là các cạnh trong . Vì cạnh bắt đầu và cạnh kết thúc của nằm trong nên hai cạnh này sẽ không nằm trong . Nói cách khác, nó là những cạnh tự do.
-
Do đó, đường đi trong đồ thị là một đường tăng luồng tương ứng với cặp ghép hiện tại . Giả thiết được chứng minh.
¶ Thuật toán
Ý tưởng chính của thuật toán là duyệt qua tất cả các đỉnh thuộc một phía của đồ thị và thực hiện tìm kiếm đường tăng luồng bắt đầu từ những đỉnh đấy. Trong bài viết này, ta quy định việc tìm kiếm đường tăng luồng sẽ bắt đầu từ các đỉnh thuộc tập bên trái.
Vì chúng ta luôn cố gắng tìm đường tăng luồng tại từng đỉnh thuộc tập bên trái, nên sau khi tìm kiếm tại tất cả các đỉnh này thì đồ thị không còn bất cứ đường tăng luồng nào. Nói cách khác, số cặp ghép tìm được lúc này là cực đại.

Vậy làm sao để tìm kiếm đường tăng luồng? Ta sẽ dễ dàng tìm kiếm chúng bằng các thuật toán tìm kiếm theo chiều sâu (DFS) / tìm kiếm theo chiều rộng (BFS) (Trong bài viết này sẽ chỉ nói về cách tìm kiếm theo chiều sâu).
Bắt đầu tìm kiếm đường tăng luồng từ đỉnh , ta sẽ duyệt qua các cạnh kề đỉnh . Gọi cạnh này là , ta có hai trường hợp của :
- Trường hợp 1: là một đỉnh tự do. Ta tìm được đường tăng luồng chứa cạnh và kết thúc quá trình tìm kiếm đường tăng luồng.
- Trường hợp 2: là đỉnh được ghép. Gọi là đỉnh đã ghép với đỉnh . Mục tiêu là cố gắng tìm đường tăng luồng đi qua các cạnh . Để làm điều đó, ta sẽ tiếp tục tìm kiếm đường tăng luồng bắt đầu từ đỉnh . Lúc này, ta sẽ có hai trường hợp xảy ra: hoặc là tìm kiếm được đường tăng luồng đi từ và kết thúc quá trình tìm kiếm đường tăng luồng, hoặc là thông báo không tìm được đường tăng luồng nếu không tồn tại đường tăng luồng nào đi từ mọi thoả mãn.
Gọi là cặp ghép hiện tại và là đường tăng luồng tương ứng với tìm được. Ta cập nhật cặp ghép bằng cách:
- Loại bỏ các cạnh trong thuộc đường tăng luồng khỏi cặp ghép.
- Thêm các cạnh ngoài thuộc đường tăng luồng vào cặp ghép.
¶ Cài đặt
Ở đây, ta có một số mảng như G, matchL, matchR, seen:
G[u]lưu tập các đỉnh kề cạnh với đỉnh .matchL[u]lưu đỉnh kề cạnh ghép với đỉnh , nếu không tồn tại, giá trị này bằng .matchR[v]lưu đỉnh kề cạnh ghép với đỉnh , nếu không tồn tại, giá trị này bằng .seen[u]lưu lại "thời gian" cuối cùng thực hiện việc tìm kiếm tại đỉnh .
Hàm kuhn(u) là hàm tìm kiếm theo chiều sâu. Hàm trả về nếu tìm được đường tăng luồng từ , và ngược lại.
Trong hàm kuhn, ta duyệt qua các đỉnh kề cạnh đỉnh . Trong hai trường hợp: hoặc là là đỉnh tự do, hoặc là là đỉnh được ghép nhưng có thể tìm được đường tăng luồng đi từ đỉnh đang ghép với . Lúc này, ta tìm được đường tăng luồng đi từ , và trước khi trả về ta sẽ thêm cặp cạnh vào cặp ghép.
Biến iteration lưu "thời gian" hiện tại. Cụ thể, vì trước khi tìm kiếm đường tăng luồng tại đỉnh , ta phải khởi tạo lại mảng đánh dấu lưu các đỉnh đã thăm trong lúc thực hiện hàm kuhn ở lần tìm kiếm đường tăng luồng tại đỉnh . Và để giảm độ phức tạp khởi tạo lại mảng đánh dấu này từ xuống , ta sử dụng mảng seen và biến iteration với định nghĩa như đã nói ở trên.
const int N = 100100;
vector<int> G[N];
int seen[N], iteration = 0;
int matchL[N], matchR[N];
// Tìm kiếm đường tăng luồng bắt đầu từ u
bool kuhn(int u) {
// Nếu "thời gian" lần cuối thăm đỉnh u bằng với "thời gian" hiện tại.
// Ta nói u đã được thăm trước đó và không tìm kiếm lần nữa.
// Ngược lại, lưu lại "thời gian" cuối cùng thăm đỉnh u bằng "thời gian" hiện tại.
// và thực hiện tìm kiếm tại u.
if(seen[u] == iteration) return 0;
seen[u] = iteration;
for(int v : G[u]) {
// Kiểm tra đỉnh v có phải là đỉnh tự do
// hoặc có cách nối khác từ đỉnh đang ghép với v
if(matchR[v] == -1 || kuhn(matchR[v])) {
// Ghi nhận cặp ghép (u, v) và thông báo có cách ghép từ đỉnh u
matchL[u] = v; matchR[v] = u;
return 1;
}
}
// Thông báo không tìm được cách ghép từ đỉnh u
return 0;
}
int matching(int M, int N, vector<pair<int, int>> E) {
// Trạng thái ban đầu chưa có cặp ghép
fill(matchL + 1, matchL + M + 1, -1);
fill(matchR + 1, matchR + N + 1, -1);
// Xây dựng danh sách kề
for(int i = 0; i < (int) E.size(); ++i) {
int u = E[i].first, v = E[i].second;
G[u].push_back(v);
}
for(int u = 1; u <= M; ++u) {
// Khởi tạo nhanh mảng đánh dấu
++iteration;
// Với mỗi đỉnh ta sẽ tìm cặp ghép từ đỉnh u
kuhn(u);
}
// Tính số cặp ghép lớn nhất
int ans = 0;
for(int u = 1; u <= M; ++u) {
if(matchL[u] != -1) { ++ans; }
}
return ans;
}
¶ Cải tiến thuật toán
Thứ tự tập cạnh quyết định rất lớn tới việc ta có nhanh chóng tìm được đường tăng luồng hay không. Do đó có một trick tối ưu thuật toán Kuhn bằng heuristic thường được sử dụng, đó là dùng random_shuffle để thay đổi thứ tự của tập cạnh ban đầu:
// Xây dựng danh sách kề
random_shuffle(E.begin(), E.end());
for(int i = 0; i < (int) E.size(); ++i) {
int u = E[i].first, v = E[i].second;
G[u].push_back(v);
}
Với cách tối ưu này, giúp thuật toán chạy đủ nhanh trong đa phần các trường hợp.
¶ Độ phức tạp
Thuật toán Kuhn sẽ thực hiện lần tìm kiếm theo chiều sâu, do đó độ phức tạp của thuật toán là .
¶ Thuật toán Hopcroft–Karp
Được cải tiến từ thuật toán Kuhn, thuật toán Hopcroft-Karp tối ưu độ phức tạp thuật toán lên đáng kể bằng việc giảm bớt số lần thực hiện tìm kiếm chiều sâu.
¶ Thuật toán
Mô hình thuật toán Hopcroft-Karp sẽ hoạt động như sau:
Bước 1: Tìm kiếm nhiều nhất số đường tăng luồng có đường đi ngắn nhất.
Bước 2: Cập nhật cặp ghép dựa vào các đường tăng luồng tìm được.
Bước 3: Kết thúc thuật toán nếu không còn đường tăng luồng nào nữa. Ngược lại, quay lại bước .
¶ Thuật toán
Giả sử ta có đồ thị , một cặp ghép và một tham số , trong đó là một số lẻ. Giả sử đường tăng luồng ngắn nhất của trong có độ dài . Ý tưởng chính của thuật toán là tìm kiếm nhiều nhất các đường tăng luồng có độ dài với . Để làm điều đó, ta sử dụng thuật toán BFS đa nguồn.
Vậy BFS đa nguồn là gì? BFS đa nguồn là một nhánh mở rộng từ thuật toán BFS. Ta sẽ bắt đầu từ nhiều đỉnh nguồn thay vì chỉ một đỉnh như BFS truyền thống. Cây thu được từ thuật toán là một đồ thị có hướng không chu trình (DAG) trong đó nếu biến đổi các cạnh của đồ thị thành vô hướng ta sẽ được một cây.
Cụ thể trong bài toán này, ta sử dụng thuật toán BFS đa nguồn để tìm kiếm khoảng cách ngắn nhất từ các đỉnh tự do thuộc tập bên trái của đồ thị tới mọi đỉnh của đồ thị.
Ta sẽ thực hiện thuật toán BFS đa nguồn trên đồ thị . Trong đó, là tập cạnh có hướng gồm hai loại:
- Các cạnh có hướng , mà cạnh .
- Các cạnh có hướng , mà cạnh .
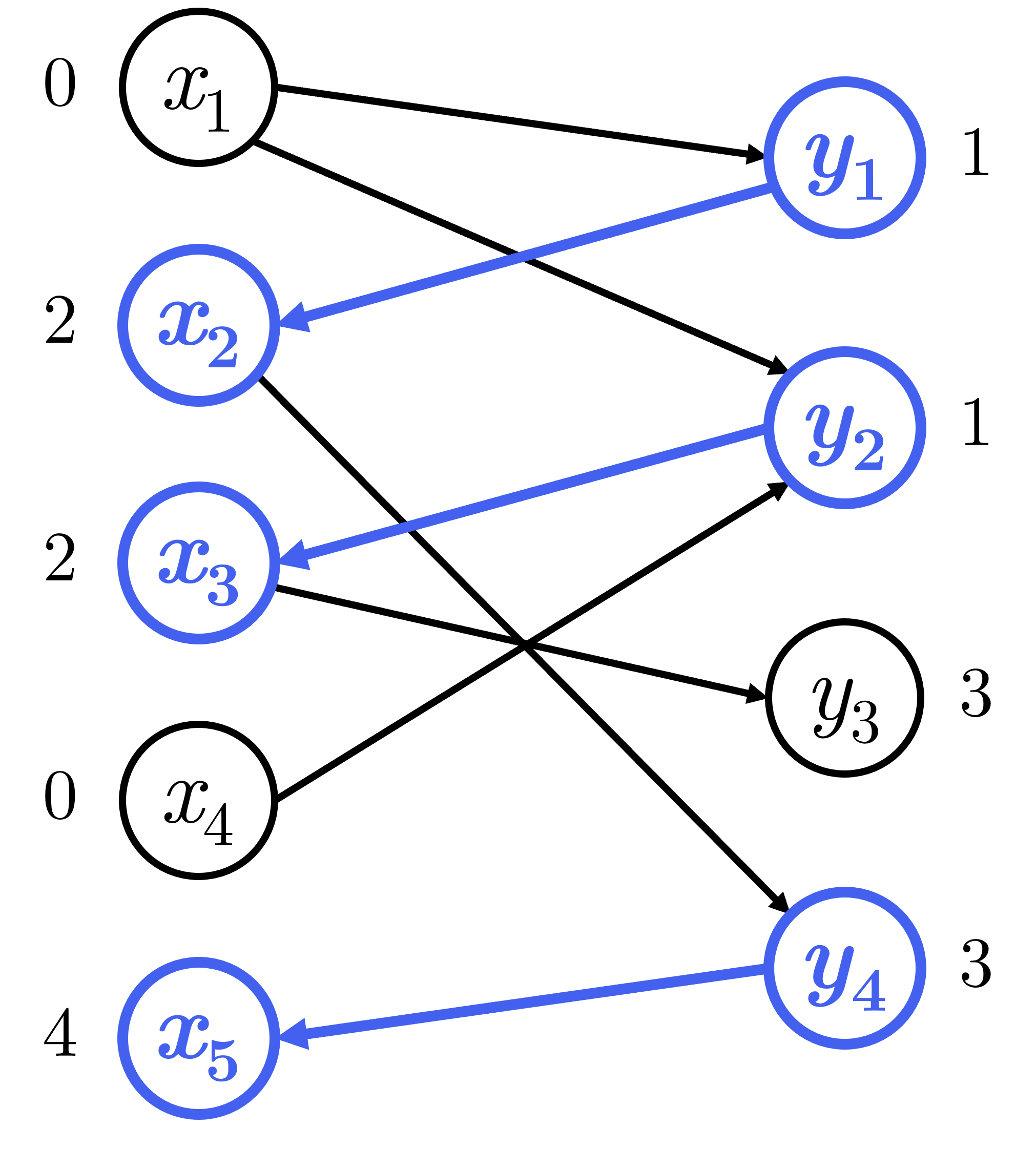
Hình 5: Thực hiện BFS đa nguồn trên đồ thị hai phía
Nếu sắp xếp lại các đỉnh của đồ thị, ta có thể thấy rõ hơn hình ảnh của một DAG như sau:
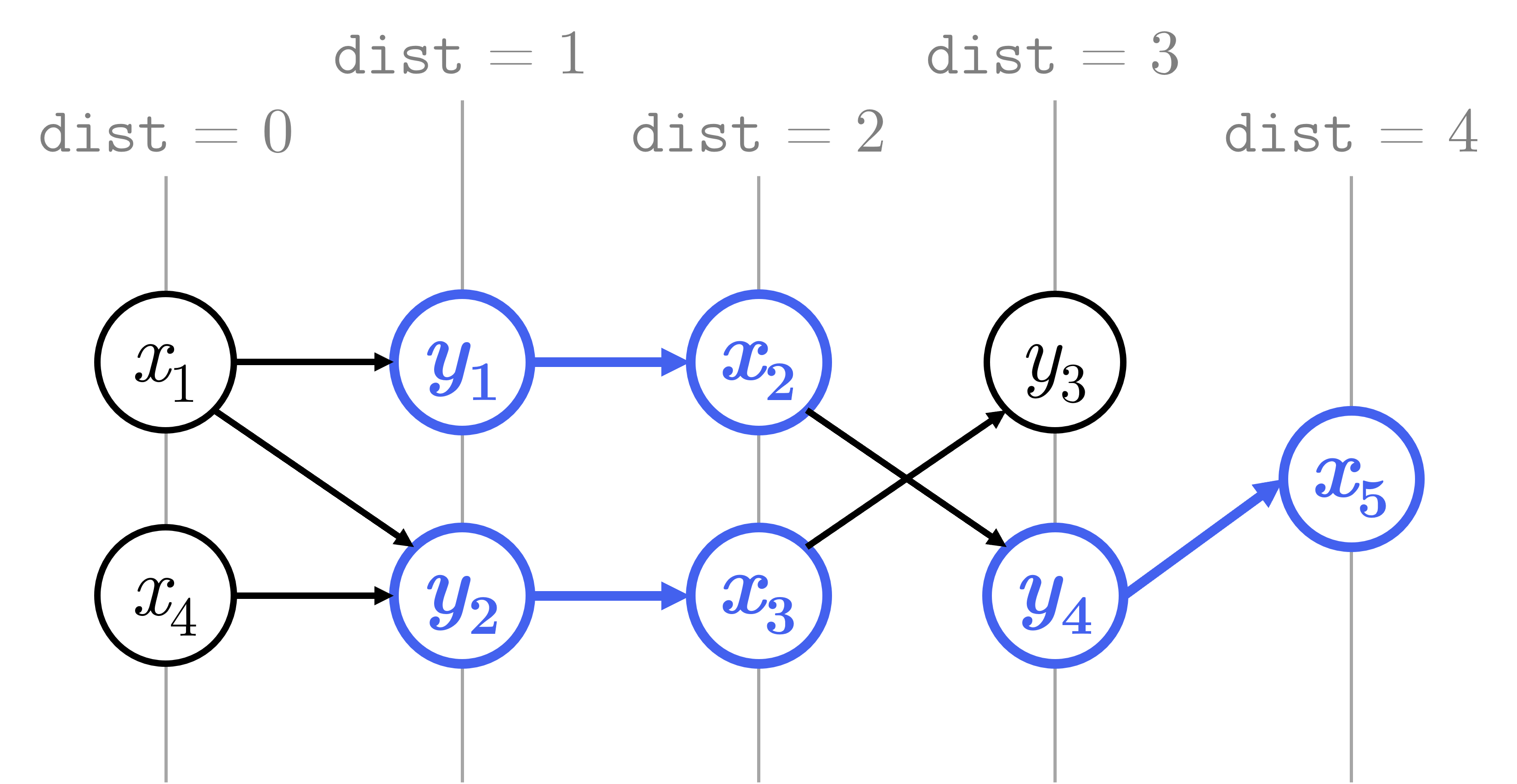
Hình 6: Đồ thị sau khi sắp xếp
Cuối cùng, ta sẽ tìm kiếm các đường tăng luồng trên cây BFS đa nguồn xây dựng được giống thuật toán Kuhn.
¶ Chứng minh các bổ đề của thuật toán
Bổ đề 2: Nếu là đường tăng luồng ngắn nhất tương ứng với cặp ghép và là đường tăng luồng bất kỳ tương ứng với . Thì . Cụ thể hơn, ta sẽ có .
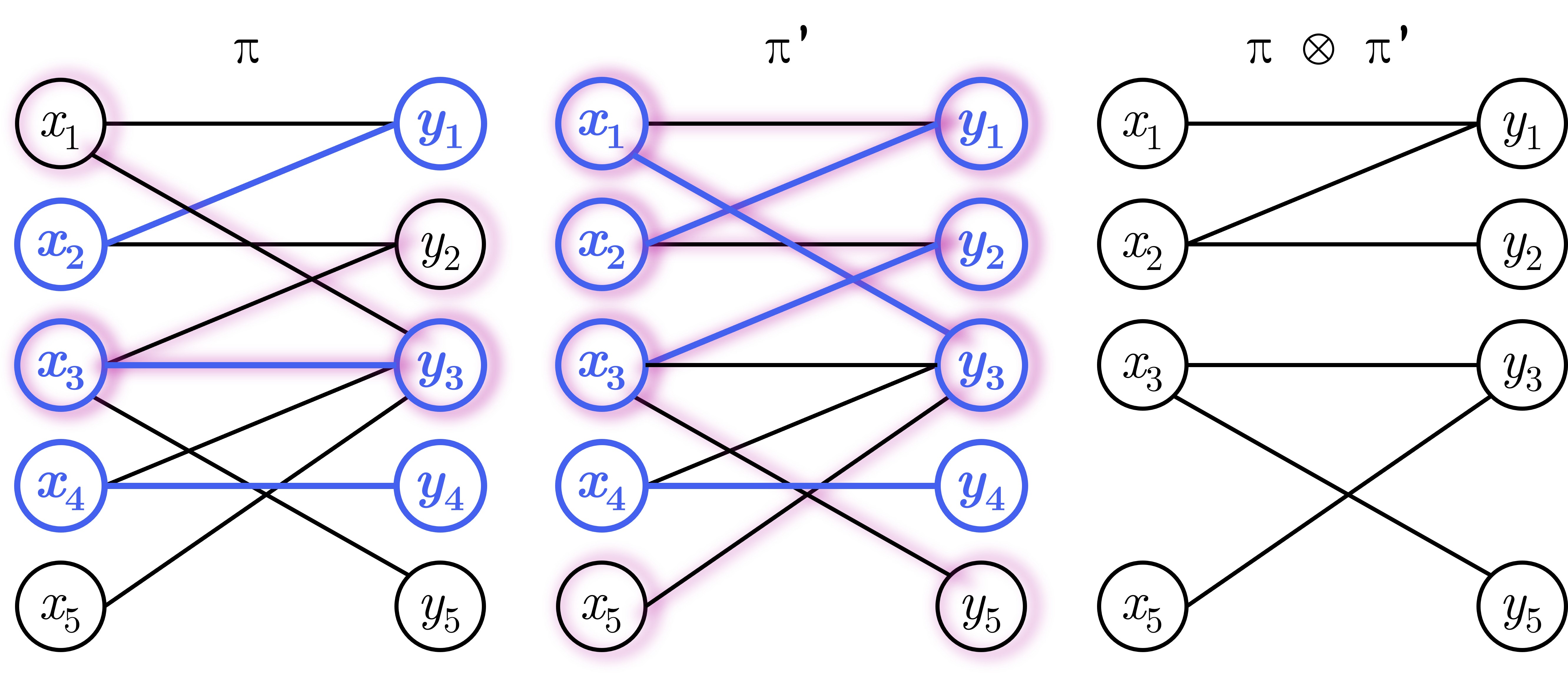
Hình 7: Hai đường tăng luồng ngắn nhất tương ứng cặp ghép M và M'
Chứng minh
Xét cặp ghép . Dễ thấy, và sẽ chứa hai đường tăng luồng không giao nhau gọi là và - Cả và đều là đường tăng luồng tương ứng với cặp ghép .
Dựa vào tính chất giao hoán, ta có:
Mặc khác, ta lại có:
Mà bởi vì là đường tăng luồng có độ dài ngắn nhất tương ứng với nên và . Chúng ta có thể kết luận được:
Theo định nghĩa, ta có công thức . Kết hợp với điều trên, ta được:
Bổ đề được chứng minh.
Từ bổ đề 2, ta rút ra được hai hệ quả sau:
-
Hệ quả 2.1: Gọi là các đường tăng luồng ngắn nhất theo thứ tự tìm được của mô hình thuật toán. Ta có .
-
Hệ quả 2.2: Ở lần thứ , khi tìm kiếm độ dài đường tăng luồng độ dài bằng với , thì độ dài đường tăng luồng ngắn nhất là .
Nhận xét 2.2.1: Ở lần tìm kiếm độ dài đường tăng luồng độ dài bằng , thì độ dài đường tăng luồng ngắn nhất là .
Bổ đề 3: Với mọi mà , thì ta có và rời nhau.
Chứng minh
Ta giả sử rằng nhưng và giao nhau. Để tiện trong việc chứng minh, giả sử thêm rằng rằng là nhỏ nhất. Khi đó, với mọi sao cho , ta có không có đỉnh chung với và .
Xét là cặp ghép sau khi thêm thêm đường tăng luồng . Lúc này, là một đường tăng luồng tương ứng với . Vì và giao nhau nhưng không thể có cùng hai đỉnh ở đầu mút (vì đó là các đỉnh tự do), nên những đỉnh chung này là một số đỉnh ở khoảng giữa.
Gọi đỉnh là một đỉnh giao của và . Vì đỉnh - một đỉnh trong , sẽ nằm ở giữa đường đi trong nên sẽ có hai cạnh kề đỉnh . Ngoài ra, đường tăng luồng có một cạnh kề đỉnh trong , gọi cạnh này là .
Vì là một cặp ghép, nên mỗi đỉnh chỉ có thể xuất hiện tối đa trong một cạnh trong . Để đảm bảo tính chất cặp ghép, sau khi thêm đường tăng luồng vào cặp ghép thì đỉnh chỉ có tối đa một cạnh kề đỉnh. Tuy nhiên, vì đỉnh trong có hai cạnh kề và nên cạnh kề trong phải là hoặc . Nói cách khác, và sẽ có ít nhất một cạnh chung ( hoặc ). Viết lại bằng công thức, ta có .
Từ bổ đề , ta có công thức:
Điều này mâu thuẫn với giả thiết rằng . Do đó, giả sử ban đầu rằng và có đỉnh chung là sai. Bổ đề được chứng minh.
Bổ đề 4: với là cặp ghép cực đại, và là cặp ghép hiện tại ở lần thực hiện tìm kiếm đường tăng luồng thứ .
Chứng minh
Từ hệ quả 2.2, ta biết được độ dài ngắn nhất đường tăng luồng tìm kiếm được là . Do đó, số đỉnh tối thiểu để tìm kiếm được đường tăng luồng là .
Mặc khác, ta lại có tổng số lượng đỉnh của đồ thị là , vì thế số đường tăng luồng còn lại cần tìm hay cũng chính là số cặp ghép còn lại bằng:
¶ Cài đặt
Để đơn giản hoá cài đặt thuật toán, ta sử dụng mảng dist với định nghĩa:
dist[u]lưu lại khoảng cách ngắn nhất giữa đỉnh tới các đỉnh tự do thuộc tập .
Ta không cần quan tâm khoảng cách ngắn nhất giữa các đỉnh thuộc tập và các đỉnh tự do thuộc tập vì ta có thể đi trực tiếp từ đỉnh tới đỉnh qua hai cạnh và .
const int N = 100100;
vector<int> G[N];
int seen[N], iteration = 0;
int dist[N], matchL[N], matchR[N];
// Tìm kiếm đường tăng luồng bắt đầu từ u
bool dfs(int u) {
// Nếu đỉnh u đã được thăm trước đó, ta sẽ không thăm lại nữa
if(seen[u] == iteration) return 0;
seen[u] = iteration;
for(int v : G[u])
// Kiểm tra đỉnh v có phải là đỉnh tự do hay không
if(matchR[v] == -1) {
matchL[u] = v; matchR[v] = u;
return 1;
}
for(int v : G[u])
// Kiểm tra đỉnh đang được ghép với v có đi được từ đỉnh u không
// và có cách nối khác từ đỉnh đang ghép với v không
if(dist[matchR[v]] == dist[u] + 1 && dfs(matchR[v])) {
// Ghi nhận cặp ghép (u, v) và thông báo có cách ghép từ đỉnh u
matchL[u] = v; matchR[v] = u;
return 1;
}
return 0;
}
int matching(int M, int N, vector<pair<int, int>> E) {
// Trạng thái ban đầu chưa có cặp ghép
fill(matchL + 1, matchL + M + 1, -1);
fill(matchR + 1, matchR + N + 1, -1);
// Xây dựng danh sách kề
for(int i = 0; i < (int) E.size(); ++i) {
int u = E[i].first, v = E[i].second;
G[u].push_back(v);
}
int ans = 0;
while(true) {
// Xây dựng các đỉnh nguồn
queue<int> q;
for(int u = 1; u <= M; ++u) {
if(matchL[u] == -1) {
dist[u] = 0; q.push(u);
} else {
dist[u] = -1;
}
}
// Thuật toán loang (BFS)
while(q.size()) {
int u = q.front(); q.pop();
for(int v : G[u]) {
if(matchR[v] != -1 && dist[matchR[v]] == -1) {
dist[matchR[v]] = dist[u] + 1;
q.push(matchR[v]);
}
}
}
// Tìm đường tăng luồng
int newMatches = 0;
++iteration;
for(int u = 1; u <= M; ++u) {
if(matchL[u] == -1) newMatches += dfs(u);
}
if(newMatches == 0) break;
// Cập nhật số lượng cặp ghép mới vào số cặp ghép hiện tại
ans += newMatches;
}
return ans;
}
¶ Độ phức tạp
Từ nhận xét 2.2.1 và bổ đề 4, ta nói kết luận rằng: số cặp ghép còn lại cần tìm không quá hay ở lần tìm kiếm thứ . Vì thế, ta sẽ đạt được cặp ghép cực đại sau thêm nhiều nhất lần thực hiện tìm kiếm đường tăng luồng. Do vậy, cặp ghép đạt cực đại trong nhiều nhất lần tìm kiếm đường tăng luồng.
Ngoài ra, ta biết rằng độ phức tạp để thực hiện tìm kiếm đường tăng luồng ở mỗi lần tìm là . Do đó, độ phức tạp của thuật toán là .
¶ Một số bài toán liên quan
¶ Bài toán tìm tập bao phủ cực tiểu
Tập bao phủ cực tiểu là tập các đỉnh mà mọi cạnh trong đồ thị chứa ít nhất một đỉnh kề thuộc tập.
Trong đồ thị bình thường, bài toán tìm kiếm tập bao phủ cực tiểu thuộc lớp NP-khó. Tuy nhiên, trong đồ thị hai phía, bài toán có thể giải quyết trong thời gian đa thức.
Thêm vào đó, bài toán tìm tập bao phủ cực tiểu và bài toán tìm cặp ghép cực đại được coi là hai bài toán liên quan tới nhau và được chứng minh bằng định lý Kőnig.
Định lý phát biểu: Số lượng cạnh trong cặp ghép cực đại đúng bằng số lượng đỉnh trong tập bao phủ cực tiểu.
¶ Bài toán phân việc
Bài toán: Cho công nhân và công việc. Thời gian người thứ hoàn thành công việc thứ là . Mỗi người chỉ làm một việc, và mỗi việc chỉ được làm bởi một người. Hỏi làm sao để phân người làm công việc để tổng thời gian hoàn thành của mọi người là nhỏ nhất.
Ràng buộc: , .
Đưa bài toán về dạng đồ thị, ta thấy rằng bài toán trở thành tìm cặp ghép cực đại với tổng chi phí cực tiểu trên đồ thị hai phía. Bằng cách sử dụng thuật toán Hungarian, ta có thể giải quyết bài toán trong .
¶ Luyện tập
- VNOJ - Company3
- VNOJ - Match1
- VNOJ - Match2
- VNOJ - Sflowerf
- ICPC - 2020 Problem J. Evacuation
- CS academy - No Prime Sum
- CF - Session in BSU
- CF - Easter Eggs
- CF - Heavy Chain Clusterization
- CF - Birthday
- CF - Matching Reduction
¶ Tham khảo
Bài viết được tham khảo từ các bài viết sau: